这个空间机器人的课设是在学期末的时候已经完成,现在在假期有时间正好做一下简要的总结和记录。另外最后一题仅仅是给出了思路(利用遗传算法 或是 粒子群算法),最终在代码实现方面并未完成,当时时间也比较紧,答辩完紧接着有考试,所以没有真正完成。(这里仅对实现代码做下简单的记录,具体内容可以看我的答辩报告)
任务
1、按固定基座空间机器人推导其运动学模型
2、按自由漂浮空间机器人推导其运动学模型
3、完成运动学正、逆解的简单运算
4、完成运动学模型的搭建,分析两者的运动空间异同
5、完成一次基座坐标系下的点到点运动规划
6、完成一次非完整运动规划(基座、关节角均期望)
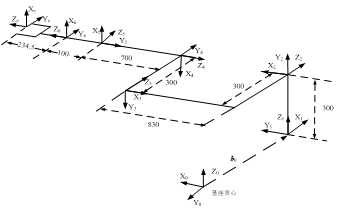
表 2 空间机器人质量特性
|
|
Sat |
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
|
|
Mass(kg) |
400 |
6 |
5 |
5 |
4 |
3 |
2 |
|
|
iai |
|
0 |
0.2702 |
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
0 |
-0.0338 |
0 |
||
|
|
0.15 |
-0.2513 |
0.15 |
-0.35 |
0 |
0.0750 |
||
|
ibi |
0.3570 |
0 |
0.5598 |
0 |
0 |
0 |
0 |
|
|
-0.0095 |
0 |
0 |
0 |
0 |
-0.0662 |
0 |
||
|
0.419 |
0.15 |
-0.0487 |
0.15 |
-0.35 |
0 |
0.1595 |
||
|
iIi (kg.m2) |
Ixx |
30 |
0.15 |
0.0926 |
0.105 |
0.2498 |
0.0330 |
5.152E-002 |
|
Iyy |
28 |
0.15 |
0.9053 |
0.105 |
0.2498 |
0.0172 |
5.152E-002 |
|
|
iIi (kg.m2) |
Ixx |
30 |
0.15 |
0.0926 |
0.105 |
0.2498 |
0.0330 |
5.152E-002 |
|
Iyy |
28 |
0.15 |
0.9053 |
0.105 |
0.2498 |
0.0172 |
5.152E-002 |
|
|
Izz |
32 |
0.075 |
0.8451 |
0.0294 |
0.0196 |
0.0260 |
2.192E-002 |
空间机械臂D-H参数表
|
连杆i |
θi |
αi |
ai (mm) |
di (mm) |
|
1 |
90° |
-90° |
0 |
0 |
|
2 |
-180° |
0 |
830 |
0 |
|
3 |
-90° |
90° |
0 |
0 |
|
4 |
0 |
-90° |
0 |
-700 |
|
5 |
180° |
90° |
0 |
0 |
|
6 |
0 |
0 |
0 |
334.5 |
%------给定初始化条件---------------------------------------------- c1=2; %学习因子1 c2=2; %学习因子2 w=0.7; %惯性权重 MaxDT=3000; %最大迭代次数 D=6; %搜索空间维数(未知数个数) M=3000; %初始化群体个体数目 %------初始化种群的个体(可以在这里限定位置和速度的范围)------------ for i=1:M for j=1:D v(i,j)=randn; %随机速度大小 x(i,j)=pi*rand; %随机初始化位置(角度) end end %------先计算各个粒子的适应度,并初始化p(i)和gbest-------------------- for i=1:M y(i,:)=x(i,:); %每个粒子对应的6维度,相当于把每个粒子给y,设y对应值此时为局部最优 p(i)=fitness(x(i,:)); %计算每个粒子距离目标位置的距离 end gbest=x(1,:); %先把第一个粒子的值设为gbest全局最优 for i=2:M if fitness(x(i,:)) < fitness(gbest) %从第二个粒子开始比较,如果有比gbest对应距离小的,则更新gbest为当前值 gbest=x(i,:); end end %------进入主要循环,按照公式依次迭代,直到满足精度要求------------ for t=1:MaxDT for i=1:M % theta(i,:)=w*theta(i,:)+c1*rand*(y(i,:)-theta(i,:))+c2*rand*(gbest-theta(i,:)); %x(i,:)=x(i,:)+theta(i,:); v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(gbest-x(i,:)); x(i,:)=x(i,:)+v(i,:); if fitness(x(i,:))<p(i) %如果迭代后此时的x(i,:)对应的距离小于原来i对应的,则当前x为局部最优 p(i)=fitness(x(i,:)); y(i,:)=x(i,:); end if p(i)<fitness(gbest) gbest=y(i,:); end end if(fitness(gbest)<0.001) break; end end %------显示计算结果 disp(‘*************************************************************‘) disp(‘粒子的最优theta值为:‘) %Solution=gbest; disp(gbest); %disp(y) %disp(fitness(x)) %Result=fitness(gbest) disp(‘*************************************************************‘) function result = fitness(x)%适应度函数,值越小说明重合度越高,就越精确 T=myfun(x); B=[0 -1 0 0;0 0 -1 -1864.5;1 0 0 0;0 0 0 1]; %result=sqrt(T(1,1)^2+T(2,1)^2+(T(3,1)-1)^2)+sqrt((T(1,2)+1)^2+(T(2,2))^2+(T(3,2))^2)+sqrt((T(1,3))^2+(T(2,3)+1)^2+(T(3,3))^2)+sqrt(T(1,4)^2+(T(2,4)+1864.5)^2+(T(3,4))^2); %result=abs(T(1,1))+abs(T(2,1))+abs(T(3,1)-1)+abs(T(1,2)+1)+abs(T(2,2))+abs(T(3,2))+abs(T(1,3))+abs(T(2,3)+1)+abs(T(3,3))+abs(T(1,4))+abs(T(2,4)+1864.5)+abs(T(3,4)); C=B-T; result=norm(C); end function T=myfun(theta) alphad1=-pi/2; a1=0;d1=0; alphad2=0; a2=830;d2=0; alphad3=pi/2; a3=0;d3=0; alphad4=-pi/2; a4=0;d4=-700; alphad5=pi/2;a5=0;d5=0; alphad6=0; a6=0;d6=334.5; i=1; A1=[cos(theta(i)),-sin(theta(i))*cos(alphad1),sin(theta(i))*sin(alphad1),a1*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad1),-cos(theta(i))*sin(alphad1),a1*sin(theta(i)); 0,sin(alphad1),cos(alphad1),d1; 0,0,0,1]; i=2; A2=[cos(theta(i)),-sin(theta(i))*cos(alphad2),sin(theta(i))*sin(alphad2),a2*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad2),-cos(theta(i))*sin(alphad2),a2*sin(theta(i)); 0,sin(alphad2),cos(alphad2),d2; 0,0,0,1]; i=3; A3=[cos(theta(i)),-sin(theta(i))*cos(alphad3),sin(theta(i))*sin(alphad3),a3*cos(theta(i)) sin(theta(i)),cos(theta(i))*cos(alphad3),-cos(theta(i))*sin(alphad3),a3*sin(theta(i)) 0,sin(alphad3),cos(alphad3),d3 0,0,0,1]; i=4; A4=[cos(theta(i)),-sin(theta(i))*cos(alphad4),sin(theta(i))*sin(alphad4),a4*cos(theta(i)) sin(theta(i)),cos(theta(i))*cos(alphad4),-cos(theta(i))*sin(alphad4),a4*sin(theta(i)) 0,sin(alphad4),cos(alphad4),d4 0,0,0,1]; i=5; A5=[cos(theta(i)),-sin(theta(i))*cos(alphad5),sin(theta(i))*sin(alphad5),a5*cos(theta(i)) sin(theta(i)),cos(theta(i))*cos(alphad5),-cos(theta(i))*sin(alphad5),a5*sin(theta(i)) 0,sin(alphad5),cos(alphad5),d5 0,0,0,1]; i=6; A6=[cos(theta(i)),-sin(theta(i))*cos(alphad6),sin(theta(i))*sin(alphad6),a6*cos(theta(i)) sin(theta(i)),cos(theta(i))*cos(alphad6),-cos(theta(i))*sin(alphad6),a6*sin(theta(i)) 0,sin(alphad6),cos(alphad6),d6 0,0,0,1]; T=A1*A2*A3*A4*A5*A6; end
第四题,搭建运动学模型以及进行运动空间的分析,这里主要是利用蒙特卡洛方法,通过大样本随机生成的theta角,利用变换矩阵来求取机械臂最终的末端位姿坐标,利用matlab中的plot3或是scatter3函数来画出三维空间的点云图,下面第一个为固定基座的第二个为自由漂浮的与固定基座的工作空间比较
clear ; N=10000; x = -pi + (2*pi).*rand([N 6]); %disp(x(1,:)); for i=1:N T=myfun(x(i,:)); p=[T(1,4),T(2,4),T(3,4)]; %{ disp(‘00000000000000000000000000000000000000000000000000000000‘); disp(p(1)); disp(p(2)); disp(p(3)); disp(‘oooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo‘); %} u(1,i)=p(1); v(1,i)=p(2); w(1,i)=p(3); %plot3(p(1),p(2),p(3),‘o‘); % scatter3(p(1),p(2),p(3),‘o‘); end figure(2) % disp(w); %disp(y); scatter3(u,v,w,‘o‘); xlabel(‘x‘); ylabel(‘y‘); zlabel(‘z‘); %plot3(u,v,w); clear u v w; function T=myfun(theta) alphad1=-pi/2; a1=0;d1=0; alphad2=0; a2=0.830;d2=0; alphad3=pi/2; a3=0;d3=0; alphad4=-pi/2; a4=0;d4=-0.700; alphad5=pi/2;a5=0;d5=0; alphad6=0; a6=0;d6=0.3345; i=1; A1=[cos(theta(i)),-sin(theta(i))*cos(alphad1),sin(theta(i))*sin(alphad1),a1*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad1),-cos(theta(i))*sin(alphad1),a1*sin(theta(i)); 0,sin(alphad1),cos(alphad1),d1; 0,0,0,1]; i=2; A2=[cos(theta(i)),-sin(theta(i))*cos(alphad2),sin(theta(i))*sin(alphad2),a2*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad2),-cos(theta(i))*sin(alphad2),a2*sin(theta(i)); 0,sin(alphad2),cos(alphad2),d2; 0,0,0,1]; i=3; A3=[cos(theta(i)),-sin(theta(i))*cos(alphad3),sin(theta(i))*sin(alphad3),a3*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad3),-cos(theta(i))*sin(alphad3),a3*sin(theta(i)); 0,sin(alphad3),cos(alphad3),d3; 0,0,0,1]; i=4; A4=[cos(theta(i)),-sin(theta(i))*cos(alphad4),sin(theta(i))*sin(alphad4),a4*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad4),-cos(theta(i))*sin(alphad4),a4*sin(theta(i)); 0,sin(alphad4),cos(alphad4),d4; 0,0,0,1]; i=5; A5=[cos(theta(i)),-sin(theta(i))*cos(alphad5),sin(theta(i))*sin(alphad5),a5*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad5),-cos(theta(i))*sin(alphad5),a5*sin(theta(i)); 0,sin(alphad5),cos(alphad5),d5 0,0,0,1]; i=6; A6=[cos(theta(i)),-sin(theta(i))*cos(alphad6),sin(theta(i))*sin(alphad6),a6*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad6),-cos(theta(i))*sin(alphad6),a6*sin(theta(i)); 0,sin(alphad6),cos(alphad6),d6; 0,0,0,1]; T=A1*A2*A3*A4*A5*A6; end
%代码中有部分数据未使用,因为还可以进一步计算
clear; m=[400,6,5,5,4,3,2]; M=sum(m); R0(1,:)=[-0.3570,0.0095,-0.4190];%初始时刻基座位置 R0(2,:)=[0,0,0.15]; R0(3,:)=[0.2702,0.2513,0.3]; R0(4,:)=[0.83,0.15,0.3]; R0(5,:)=[1.18,0,0.3]; R0(6,:)=[1.5638,0,0.3]; R0(7,:)=[1.705,0,0]; rg=0; for i=1:7 rg=rg+m(i)*R0(i,:); end rg=rg/M; b0=[0.357,-0.0095,0.419]; a(1,:)=[0,0,0.15]; b(1,:)=[0,0,0.15]; a(2,:)=[0.2702,0.2513,0]; b(2,:)=[0.5598,0.0487,0]; a(3,:)=[0,-0.15,0]; b(3,:)=[0,-0.15,0]; a(4,:)=[0.35,0,0]; b(4,:)=[0.35,0,0]; a(5,:)=[0.0338,0,0]; b(5,:)=[0.0662,0,0]; a(6,:)=[0.075,0,0]; b(6,:)=[0.1595,0,0]; b0_=m(1)/M*b0; for i=1:6 a_(i,:)=sum(m(1:i))/M*a(i,:); b_(i,:)=sum(m(1:i+1))/M*b(i,:); end B0=b0-rg;%rg系统质心 ,b0基座矢近, N=10000; x = -pi + (2*pi).*rand([N 6]); for i=1:N T=myfun1(x(i,:),B0); p=[T(1,4),T(2,4),T(3,4)]; u(1,i)=p(1); v(1,i)=p(2); w(1,i)=p(3); end clear ; N=10000; x = -pi + (2*pi).*rand([N 6]); %disp(x(1,:)); for i=1:N T=myfun(x(i,:)); p=[T(1,4),T(2,4),T(3,4)]; %{ disp(‘00000000000000000000000000000000000000000000000000000000‘); disp(p(1)); disp(p(2)); disp(p(3)); disp(‘oooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo‘); %} u(1,i)=p(1); v(1,i)=p(2); w(1,i)=p(3); %plot3(p(1),p(2),p(3),‘o‘); % scatter3(p(1),p(2),p(3),‘o‘); end figure(1) plot3(u,v,w,‘o‘,u,v,w,‘o‘); %figure(2) %scatter3(u,v,w,‘*‘); xlabel(‘x‘); ylabel(‘y‘); zlabel(‘z‘); %plot3(u,v,w); clear u v w; function T=myfun1(theta,B0) alphad1=-pi/2; a1=0;d1=0; alphad2=0; a2=0.80265;d2=0;%830*(m(1)+m(2)+m(3))/M alphad3=pi/2; a3=0;d3=0; alphad4=-pi/2; a4=0;d4=-0.700; alphad5=pi/2;a5=0;d5=0; alphad6=0; a6=0;d6=0.3345; for t=1:10 q = rand(1,4); k = q/sum(q(:)); n=sqrt(abs(k(1))); q1=-sqrt(abs(k(2))); q2=sqrt(abs(k(3))); q3=-sqrt(abs(k(4))); A0=[q1^2-q2^2-q3^2+n^2 2*(q1*q2-q3*n) 2*(q1*q3+q2*n) B0(1) 2*(q1*q2+q3*n) -q1^2+q2^2-q3^2+n^2 2*(q2*q3-q1*n) B0(2) 2*(q1*q3-q2*n) 2*(q2*q3+q1*n) -q1^2-q2^2+q3^2+n^2 B0(3) 0 0 0 1]; end i=1; A1=[cos(theta(i)),-sin(theta(i))*cos(alphad1),sin(theta(i))*sin(alphad1),a1*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad1),-cos(theta(i))*sin(alphad1),a1*sin(theta(i)); 0,sin(alphad1),cos(alphad1),d1; 0,0,0,1]; i=2; A2=[cos(theta(i)),-sin(theta(i))*cos(alphad2),sin(theta(i))*sin(alphad2),a2*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad2),-cos(theta(i))*sin(alphad2),a2*sin(theta(i)); 0,sin(alphad2),cos(alphad2),d2; 0,0,0,1]; i=3; A3=[cos(theta(i)),-sin(theta(i))*cos(alphad3),sin(theta(i))*sin(alphad3),a3*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad3),-cos(theta(i))*sin(alphad3),a3*sin(theta(i)); 0,sin(alphad3),cos(alphad3),d3; 0,0,0,1]; i=4; A4=[cos(theta(i)),-sin(theta(i))*cos(alphad4),sin(theta(i))*sin(alphad4),a4*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad4),-cos(theta(i))*sin(alphad4),a4*sin(theta(i)); 0,sin(alphad4),cos(alphad4),d4; 0,0,0,1]; i=5; A5=[cos(theta(i)),-sin(theta(i))*cos(alphad5),sin(theta(i))*sin(alphad5),a5*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad5),-cos(theta(i))*sin(alphad5),a5*sin(theta(i)); 0,sin(alphad5),cos(alphad5),d5 0,0,0,1]; i=6; A6=[cos(theta(i)),-sin(theta(i))*cos(alphad6),sin(theta(i))*sin(alphad6),a6*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad6),-cos(theta(i))*sin(alphad6),a6*sin(theta(i)); 0,sin(alphad6),cos(alphad6),d6; 0,0,0,1]; T=A0*A1*A2*A3*A4*A5*A6; disp(A0) ; end function T=myfun(theta) alphad1=-pi/2; a1=0;d1=0; alphad2=0; a2=0.830;d2=0; alphad3=pi/2; a3=0;d3=0; alphad4=-pi/2; a4=0;d4=-0.700; alphad5=pi/2;a5=0;d5=0; alphad6=0; a6=0;d6=0.3345; i=1; A1=[cos(theta(i)),-sin(theta(i))*cos(alphad1),sin(theta(i))*sin(alphad1),a1*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad1),-cos(theta(i))*sin(alphad1),a1*sin(theta(i)); 0,sin(alphad1),cos(alphad1),d1; 0,0,0,1]; i=2; A2=[cos(theta(i)),-sin(theta(i))*cos(alphad2),sin(theta(i))*sin(alphad2),a2*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad2),-cos(theta(i))*sin(alphad2),a2*sin(theta(i)); 0,sin(alphad2),cos(alphad2),d2; 0,0,0,1]; i=3; A3=[cos(theta(i)),-sin(theta(i))*cos(alphad3),sin(theta(i))*sin(alphad3),a3*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad3),-cos(theta(i))*sin(alphad3),a3*sin(theta(i)); 0,sin(alphad3),cos(alphad3),d3; 0,0,0,1]; i=4; A4=[cos(theta(i)),-sin(theta(i))*cos(alphad4),sin(theta(i))*sin(alphad4),a4*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad4),-cos(theta(i))*sin(alphad4),a4*sin(theta(i)); 0,sin(alphad4),cos(alphad4),d4; 0,0,0,1]; i=5; A5=[cos(theta(i)),-sin(theta(i))*cos(alphad5),sin(theta(i))*sin(alphad5),a5*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad5),-cos(theta(i))*sin(alphad5),a5*sin(theta(i)); 0,sin(alphad5),cos(alphad5),d5 0,0,0,1]; i=6; A6=[cos(theta(i)),-sin(theta(i))*cos(alphad6),sin(theta(i))*sin(alphad6),a6*cos(theta(i)); sin(theta(i)),cos(theta(i))*cos(alphad6),-cos(theta(i))*sin(alphad6),a6*sin(theta(i)); 0,sin(alphad6),cos(alphad6),d6; 0,0,0,1]; T=A1*A2*A3*A4*A5*A6; end
第5题比较简单,只是做一下简单的插值,这里使用的是5阶多项式插值
close all; clear all; q0(1)=1.5708; q0(2)=-3.1416; q0(3)=-1.5708; q0(4)=0; q0(5)=3.1416; q0(6)=0; qf(1)=1.5741; qf(2)=1.9527; qf(3)=0.4579; qf(4)=1.5558; qf(5)=3.1312; qf(6)=1.5547; t=[0,0.1,10]; a=Planning(q0,qf,10) function a=Planning(q0,qf,t) a=ones(6,6); for i=1:6 a(i,1)=q0(i); a(i,2)=0; a(i,3)=0; a(i,4)=(20*qf(i)-20*q0(i))/t^3/2; a(i,5)=(-30*qf(i)+30*q0(i))/t^4/2; a(i,6)=(12*qf(i)-12*q0(i))/t^5/2; end end close all; clear all; t=0:0.1:10; for i=1:101 q1(i)=1.5708; end q2=-3.1416+0.0509*power(t,3)-0.0076*power(t,4)+0.0003*power(t,5); q3=-1.5708+0.0203*power(t,3)-0.0030*power(t,4)+0.0001*power(t,5); q4=0.0156*power(t,3)-0.0023*power(t,4)+0.0001*power(t,5); q5=3.1416-0.0001*power(t,3); q6=0.0155*power(t,3)-0.0023*power(t,4)+0.0001*power(t,5); figure(1) plot(t,q1) xlabel(‘时间‘); ylabel(‘关节角1‘); figure(2) plot(t,q2) xlabel(‘时间‘); ylabel(‘关节角2‘); figure(3) plot(t,q3) xlabel(‘时间‘); ylabel(‘关节角3‘); figure(4) plot(t,q4) xlabel(‘时间‘); ylabel(‘关节角4‘); figure(5) plot(t,q5) xlabel(‘时间‘); ylabel(‘关节角5‘); figure(6) plot(t,q6) xlabel(‘时间‘); ylabel(‘关节角6‘);
