题目
BOI 2005 Day 1
Maze
Pasvalys Language: ENG
Lithuania
7.5.2005 Page 1 of 2 MAZE
Maze (Lithuania)
Consider the following maze made of equilateral triangles:
Each vertex is described by two coordinates x and y as in the picture. Some of the edges
have a white or a black circle on them. There are two major rules that control movement
within the maze:
§ it is only allowed to pass edges with circles on them.
§ while walking through the maze it is obligatory to alternate white and black
circles; i.e. it is only allowed to pass an edge with white circle if the last circle
passed was black and vice versa. It is allowed to pass an edge with either black or
white circle on it during the first move.
TASK
Write a program to find the length of the shortest path from the entrance point to the exit
in the maze. The length of the path is defined as the number of edges (or circles) passed.
You may assume that such path always exists.
INPUT
The input file name is MAZE.IN The first line contains two integers W and H which are
the width and the height of the maze respectively (1 £ W, H £ 500). The second line
consists of four integer values: X1 Y1 X2 Y2 (0 £ X1, X2 £ W; 0 £ Y1, Y2 £ H ). (X1, Y1) are
the coordinates of the entry point in the maze and (X2, Y2) are the exit coordinates.
The next 2H+1 lines provide the description of the edges: odd lines (3rd, 5th, etc) describe
horizontal edges, and even lines (4th, 6th, etc) describe non-horizontal ones. Each line
consists of a string of characters n, w and b, where n means, that there is no circle on the
edge, and w or b means that there is white or black circle on the edge respectively. There
are no spaces between these characters. Naturally, odd lines consist of exactly W
characters, and even lines consist of exactly 2W+1 characters.
BOI 2005 Day 1
Maze
Pasvalys Language: ENG
Lithuania
7.5.2005 Page 2 of 2 MAZE
OUTPUT
Your program should output a single integer (the length of the shortest path from entrance
point to the exit in the maze) in the first (and the only) line of the file MAZE.OUT.
EXAMPLES
INPUT OUTPUT COMMENTS
2 1
0 0 2 1
bb
nwwnw
bn
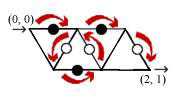
6 A simple maze. One possible shortest path is
this:
(0, 0) à (1, 0) à (0, 1) à (1, 1) à (1, 0) à
(2, 0) à (2, 1)
Here is the illustration of the maze and the
shortest path:
INPUT OUTPUT COMMENTS
5 4
0 2 5 2
nnbnn
nnnwwbwnnnn
nbbbn
nnwbwwbwwnn
bwwww
nnbwbbwwbnn
nwwwn
nnnnbwbbnnn
nnwnn
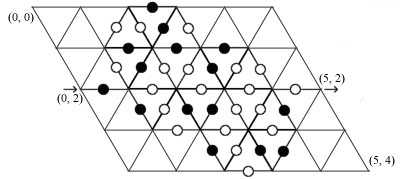
22 This is the description of the maze given in the
picture on the first page. The shortest path is
this:
(0, 2) à (1, 2) à (1, 1) à (2, 1) à (2, 0) à
(3, 0) à (3, 1) à (3, 2) à (4, 1) à (3, 1) à
(3, 0) à (2, 0) à (2, 1) à (1, 1) à (1, 2) à
(1, 3) à (2, 3) à (2, 4) à (3, 4) à (3, 3) à
(4, 3) à (4, 2) à (5, 2)
(Length: 22)
分析
其实这道题就是有些变化的最短路径问题,也就是这道题对于这个“路径”有一定的要求:必须黑白交替行进。
这道题比较令人头疼的难点在于这个坐标。首先这不是正方形的格子,而是等边三角形,并且坐标表示方法也和习惯有些不同。通常我们写SPFA都会用到的是这个点的“代号”。这里用坐标就会显得比较难受。可以硬着头皮直接带着坐标写,但是我本着程序员十分钟做完的事情宁愿花一个小时来写程序解决的精神,我在读入的时候就把所有的点预处理好,以“代号”的形式来存储。从左上角,先往右,再往下,依次给每个点标号。这样做肯定有些烧脑,要理清点、边之间的关系。(读入边的颜色,所以要将边转化为点的坐标再转化为点的代号,然后进行建边)
这样一来,所有事情就像我们往常做的一样了。裸着SPFA,在其中对于边的颜色加一个小小的判断(没有颜色的边我直接就没有添加,因为肯定不会经过)。
程序
1 #include <bits/stdc++.h> 2 using namespace std; 3 struct point 4 { 5 int x,y; 6 }A,B; 7 struct edge 8 { 9 int Next, Aim; 10 bool Color; 11 // TRUE: Black 12 // FALSE: White 13 }Edge[501*501*2]; 14 int W, H, EdgeCount, Head[501*501], start, target; 15 int dist[501*501+1][2]; 16 char C; 17 void Insert(int u, int v, char color) 18 { 19 if (color == ‘w‘) 20 { 21 Edge[++EdgeCount] = (edge){Head[u], v, false}; 22 Head[u] = EdgeCount; 23 Edge[++EdgeCount] = (edge){Head[v], u, false}; 24 Head[v] = EdgeCount; 25 } 26 if (color == ‘b‘) 27 { 28 Edge[++EdgeCount] = (edge){Head[u], v, true}; 29 Head[u] = EdgeCount; 30 Edge[++EdgeCount] = (edge){Head[v], u, true}; 31 Head[v] = EdgeCount; 32 } 33 } 34 void SPFA() 35 { 36 //0: White 37 //1: Black 38 //freopen("maze.in","r",stdin); 39 //freopen("maze.out","w",stdout); 40 memset(dist, 0x3F, sizeof(dist)); 41 queue<int> Q; 42 Q.push(start); 43 dist[start][0] = dist[start][1] = 0; 44 while(!Q.empty()) 45 { 46 int u = Q.front(); 47 Q.pop(); 48 for (int i = Head[u]; i; i = Edge[i].Next) 49 { 50 int v = Edge[i].Aim; 51 if (Edge[i].Color) 52 { 53 if (dist[u][0]+1<dist[v][1]) 54 { 55 dist[v][1] = dist[u][0]+1; 56 Q.push(v); 57 } 58 } 59 else 60 { 61 if (dist[u][1]+1<dist[v][0]) 62 { 63 dist[v][0] = dist[u][1]+1; 64 Q.push(v); 65 } 66 } 67 } 68 } 69 } 70 /* 71 2 1 72 0 0 2 1 73 bb 74 nwwnw 75 bn 76 */ 77 int main() 78 { 79 cin >> W >> H; 80 cin >> A.x >> A.y >> B.x >> B.y; 81 start = A.y*(W+1)+A.x+1, target = B.y*(W+1)+B.x+1; 82 for (int i = 1; i <= 2*H+1; i++) 83 { 84 if (i % 2) 85 { 86 for (int j = 1; j <= W; j++) 87 { 88 cin >> C; 89 int p1 = (i-1)/2*(W+1)+j, p2 = (i-1)/2*(W+1)+j+1; 90 Insert(p1,p2,C); 91 } 92 } 93 else 94 { 95 for (int j = 1; j <= 2*W+1; j++) 96 { 97 cin >> C; 98 if (j % 2) 99 { 100 int p1 = (i/2-1)*(W+1)+(j+1)/2, p2 = i/2*(W+1)+(j+1)/2; 101 Insert(p1,p2,C); 102 } 103 else 104 { 105 int p1 = (i/2-1)*(W+1)+j/2+1, p2 = i/2*(W+1)+j/2; 106 Insert(p1,p2,C); 107 } 108 } 109 } 110 } 111 SPFA(); 112 /* 113 for (int i = 1; i <= (W+1)*(H+1); i++) 114 cout << dist[i][0] << " " << dist[i][1] << endl; 115 */ 116 cout << min(dist[target][0],dist[target][1]) << endl; 117 return 0; 118 }
