一、性质
①节点非黑即红。
②根节点为黑色。
③叶节点的孩子为黑色空节点。(NIL节点)
④红色节点的孩子为黑色。
⑤从任何节点到叶节点的路径包含相同数目的黑色节点。
解释:红黑树是2-3-4树的等价数据结构,黑色节点等价于的3孩子,红色节点等价于2孩子和4孩子。
二、旋转
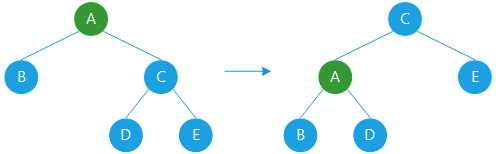
①左旋
图示以A为轴节点进行左旋。
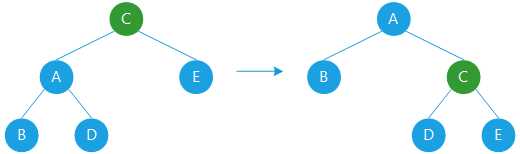
②右旋
图示以C为轴节点进行右旋。
三、插入
将红黑树作为一棵搜索树进行插入,具体过程如下:(根节点为初始当前节点)
①若插入节点大于当前节点,若当前节点的右孩子为空,则将插入节点作为当前节点的右孩子插入,否则当前节点变为其右孩子。
②若插入节点小于当前节点,若当前节点的左孩子为空,则将插入节点作为当前节点的左孩子插入,否则当前节点变为其左孩子。
③若插入节点等于当前节点,则插入失败,搜索树不允许存在相等节点。
插入完成后默认将插入节点涂红,对红黑树进行调整使其恢复平衡,存在如下情况:(插入节点为初始当前节点)
①若当前节点的父亲为黑色。结束调整。
②若当前节点的父亲为红色,叔叔为黑色。
㈠若父亲为左孩子,当前节点为右孩子,则当前节点变为父亲,以父亲为轴进行左旋。转化为情况⑶
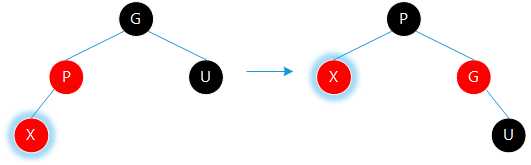
㈡若父亲为右孩子,当前节点为左孩子,则当前节点变为父亲,以父亲为轴进行右旋。转化为情况⑷
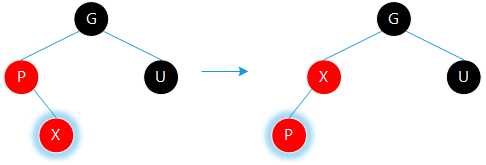
㈢若父亲为左孩子,当前节点为左孩子,则将父亲涂黑,祖父涂红,以祖父为轴进行右旋。调整结束。
㈣若父亲为右孩子,当前节点为右孩子,则将父亲涂黑,祖父涂红,以祖父为轴进行左旋。调整结束。
③若当前节点的父亲为红色,叔叔为红色。则将父亲和叔叔涂红,祖父涂红,设置祖父为当前节点继续回溯。
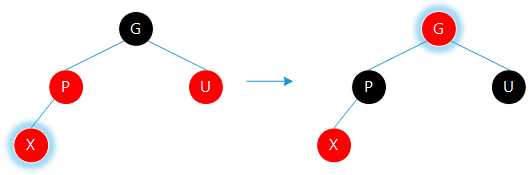
调整思路:将红色转移到合适的位置。
四、删除
将红黑树作为一棵搜索树进行删除,存在如下情况:
①若删除节点没有孩子,则直接删除。
②若删除节点只有一个孩子,则直接删除后其孩子代替其位置。
③若删除节点有两个孩子,则将其数据与后继节点(左子树最大节点或右子树最小节点)交换,问题转换为其后继节点的删除。
删除完成后对红黑树进行调整使其恢复平衡,存在如下情况:
①若删除节点为红色。结束调整。
②若删除节点为黑色,且只有一个孩子。则将孩子涂黑,结束调整。(根据性质⑤可知孩子必为红色)
③若删除节点为黑色,且没有孩子。存在如下情况:(删除节点的叶节点为初始当前节点)
㈠若当前节点的兄弟为黑色,存在红色侄子。
⑴若当前节点为左孩子,右侄子为红色。则交换兄弟与父亲的颜色,右侄子涂黑,以父亲为轴左旋,结束调整。
⑵若当前节点为右孩子,左侄子为红色。则交换兄弟与父亲的颜色,左侄子涂黑,以父亲为轴右旋,结束调整。
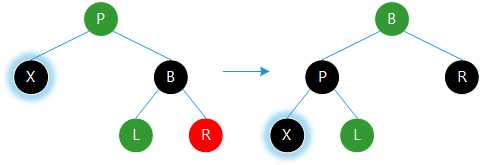
注:绿色代表可为红色,也可为黑色。
⑶若当前节点为左孩子,右侄子为黑色,左侄子为红色。则左侄子涂为父亲的颜色,父亲涂黑,依次以兄弟为轴右旋、以父亲为轴左旋,结束调整。
⑷若当前节点为右孩子,左侄子为黑色,右侄子为红色。则右侄子涂为父亲的颜色,父亲涂黑,依次以兄弟为轴左旋、以父亲为轴右旋,结束调整。
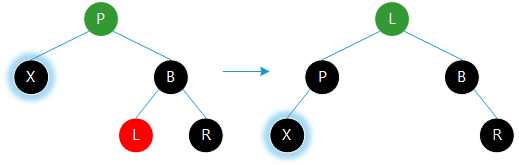
㈡若当前节点的兄弟、侄子为黑色,父亲为红色。则将兄弟涂红,父亲涂黑,结束调整。
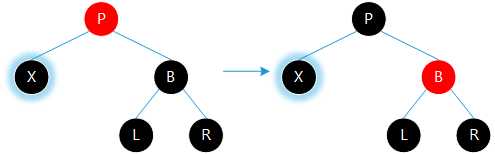
㈢若当前节点的兄弟、侄子和父亲均为黑色。则将兄弟节点涂红,设置父亲为当前节点继续回溯。
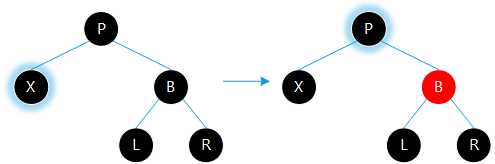
㈣若当前节点的兄弟为红色。则将兄弟涂黑,父亲涂红,以父亲为轴进行旋转。转换黑色兄弟节点的情况。
⑴若当前节点为左孩子,则父亲进行左旋。
⑵若当前节点为右孩子,则父亲进行右旋。
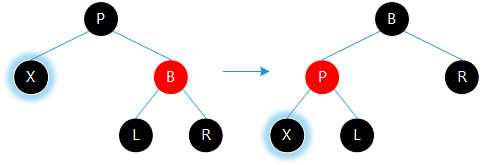
调整思路:补充路径中缺失的黑色。
五、实现
public class TreeSet { private static final boolean RED = false; private static final boolean BLACK = true; private static class Node { int key; boolean color; Node parent; Node left; Node right; Node(int key, boolean color, Node parent, Node left, Node right) { this.key = key; this.color = color; this.parent = parent; this.left = left; this.right = right; } } private final Node NIL; private Node ROOT; public TreeSet() { NIL = new Node(Integer.MIN_VALUE, BLACK, null, null, null); NIL.left = NIL; NIL.right = NIL; ROOT = NIL; } private void leftRotate(Node x) { Node y = x.right; x.right = y.left; y.left.parent = x; y.parent = x.parent; if (x.parent == NIL) ROOT = y; else { if (x == x.parent.left) x.parent.left = y; else x.parent.right = y; } y.left = x; x.parent = y; } private void rightRotate(Node y) { Node x = y.left; y.left = x.right; x.right.parent = y; x.parent = y.parent; if (y.parent == NIL) ROOT = x; else { if (y == y.parent.right) y.parent.right = x; else y.parent.left = x; } x.right = y; y.parent = x; } private Node find(int key) { Node x = ROOT; while (x != NIL) { if (key < x.key) x = x.left; else if (key > x.key) x = x.right; else break; } return x; } private Node minimum(Node x) { while (x.left != NIL) x = x.left; return x; } public boolean contains(int key) { return find(key) != NIL; } public boolean add(int key) { if (find(key) != NIL) return false; Node z = new Node(key, RED, NIL, NIL, NIL); Node y = NIL; Node x = ROOT; while (x != NIL) { y = x; if (key < x.key) x = x.left; else x = x.right; } z.parent = y; if (y == NIL) ROOT = z; else { if (key < y.key) y.left = z; else y.right = z; } fixUpAdd(z); return true; } private void fixUpAdd(Node z) { Node p = z.parent; while (p.color == RED) { Node g = p.parent; if (p == g.left) { Node u = g.right; if (u.color == RED) { p.color = BLACK; u.color = BLACK; g.color = RED; z = g; } else { if (z == p.right) { z = p; leftRotate(z); } p.color = BLACK; g.color = RED; rightRotate(g); } } else { Node u = g.left; if (u.color == RED) { p.color = BLACK; u.color = BLACK; g.color = RED; z = g; } else { if (z == p.left) { z = p; rightRotate(z); } p.color = BLACK; g.color = RED; leftRotate(g); } } p = z.parent; } ROOT.color = BLACK; } public boolean remove(int key) { Node z = find(key); if (z == NIL) return false; Node y = (z.left == NIL || z.right == NIL) ? z : minimum(z.right); Node x = (y.left != NIL) ? y.left : y.right; x.parent = y.parent; if (y.parent == NIL) ROOT = x; else { if (y == y.parent.left) y.parent.left = x; else y.parent.right = x; } z.key = y.key; if (y.color == BLACK) fixUpRemove(x); return true; } private void fixUpRemove(Node x) { while (x != ROOT && x.color == BLACK) { Node p = x.parent; if (x == p.left) { Node b = p.right; if (b.color == RED) { b.color = BLACK; p.color = RED; leftRotate(x.parent); p = x.parent; b = p.right; } if (b.left.color == BLACK && b.right.color == BLACK) { b.color = RED; x = x.parent; } else { if (b.right.color == BLACK) { b.left.color = BLACK; b.color = RED; rightRotate(b); p = x.parent; b = p.right; } b.color = x.parent.color; p.color = BLACK; b.right.color = BLACK; leftRotate(p); x = ROOT; } } else { Node b = p.left; if (b.color == RED) { b.color = BLACK; p.color = RED; rightRotate(p); p = x.parent; b = p.left; } if (b.right.color == BLACK && b.left.color == BLACK) { b.color = RED; x = p; } else { if (b.left.color == BLACK) { b.right.color = BLACK; b.color = RED; leftRotate(b); p = x.parent; b = p.left; } b.color = p.color; p.color = BLACK; b.left.color = BLACK; rightRotate(p); x = ROOT; } } } x.color = BLACK; } public void inOrder(Node x) { if (x != NIL) { inOrder(x.left); System.out.println(x.key); inOrder(x.right); } } public static void main(String[] args) { int max = 100000; TreeSet set = new TreeSet(); for (int i = 0; i < max; i++) set.add(i); for (int i = 10; i < max; i++) set.remove(i); set.inOrder(set.ROOT); } }
