Description
问题描述以及测试样例在这:HDU#2191
思路
这道题其实就是多重背包问题,即有 N 种物品和一个容量为 V 的背包,第 i 种物品最多有 n[i] 件可用,每件费用是 c[i] ,价值是 w[i] ,求哪些物品装入背包可以使得这些物品的费用总和不超过背包容量,且价值总和最大。在这道题中,背包容量是经费,费用是每种米的价格,价值是每种米的重量,求用给定的经费买米,使得买到米的总重量最大,注意经费是可以剩余的。
其实多重背包问题和完全背包问题非常相似,只不过前者的物品是有限件而后者物品是无限件。我们可以把完全背包的状态转移方程改造一下而得到多重背包的状态转移方程,如下:
dp[i][j] = max { dp[i-1][v-k*c[i]] + k*w[i] | 0 <= k <= n[i] }
算法通过穷举 k 而得到所有的解,然后在从其中调出最大的。我们根据它很容易就可以写出算法,时间复杂度为 O( V·∑n[i] ) :

#include<iostream> #include<algorithm> using namespace std; const int MAX_N = 100; //经费价格上限 const int MAX_M = 100; //大米种类上限 int price[MAX_M+1]; //价格 int weight[MAX_M+1]; //重量 int num[MAX_M+1]; //袋数 int dp[MAX_M+1][MAX_N+1] = {0}; //最大重量 int main(void) { int test_num; cin >> test_num; while (test_num--) { int n, m; //经费金额, 大米种类 cin >> n >> m; for (int i = 1; i <= m; ++i) { cin >> price[i] >> weight[i] >> num[i]; } //用j经费买前i种米,能买到的最大总重量 for (int i = 1; i <= m; i++){ for (int j = 1; j <= n; j++) { int max_weight = 0; for (int k = 0; k <= num[i]; k++) { if (j-k*price[i] >= 0) { if (max_weight < dp[i-1][j-k*price[i]] + k*weight[i] ) { max_weight = dp[i-1][j-k*price[i]] + k*weight[i]; } } } dp[i][j] = max_weight; } } cout << dp[m][n] << endl; } return 0; }
然而,它和自顶向下的递归算法一比,时间和空间并没有得到优化,所以我先从空间上去优化这个算法。
由于01背包问题和完全背包问题都有一维数组实现的算法,那么我们可以试着把多重背包问题转化成其中一个问题再进行求解。我先把它转化成好写且好理解的01背包问题。在01背包问题中需要我们以“件”为单位而不是以“种”为单位去看待物品,所以需要把一种物品拆分成多件物品。
如何拆分呢?
在多重背包里,直接把第 i 种物品拆分成 n[i] 件就好啦。
额外再说个完全背包问题中拆分物品的方法。如果物品的个数是 N ,背包的容量是 V ,第 i 种物品的费用是 cost[i] ,那么应该把第 i 种物品拆分成 V/cost[i] 件。举个例子,如果物品个数是 3 ,背包的容量是 5 ,那么拆分前的物品序列是下面图左,拆分后的物品序列是下面的图右:
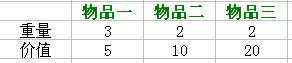

拆分好之后,就直接套用一维滚动数组解决01背包问题的算法即可,空间复杂度优化到为 O(V) :

#include<iostream> #include<algorithm> #include<cstring> using namespace std; const int MAX_N = 100; //经费价格上限 const int MAX_M = 100; //大米种类上限 int price[MAX_M+1]; //价格 int weight[MAX_M+1]; //重量 int num[MAX_M+1]; //袋数 int dp[MAX_N+1]; //最大重量 int main(void) { int test_num; cin >> test_num; while (test_num--) { int n, m; //经费金额, 大米种类 cin >> n >> m; for (int i = 1; i <= m; ++i) { cin >> price[i] >> weight[i] >> num[i]; } //初始化dp memset(dp, 0, sizeof(dp)); //用j经费买前i种米,能买到的最大总重量 for (int i = 1; i <= m; i++){ //对第i种米进行num[i]次01选择 for (int k = 1; k <= num[i]; k++) { for (int j = n; j >= price[i]; j--) { //要么选,要么不选 dp[j] = std::max(dp[j], dp[j-price[i]] + weight[i] ); } } } /* cout << "检查中" << endl; for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++){ cout << dp[i][j] << " "; } cout << endl; } */ cout << dp[n] << endl; } return 0; }
如何优化时间复杂度呢?这个我暂时没有思路,之后若有了话再继续写博。

