在【乔明达的省选专题】里面有很多这样的解题技巧:
把Σ*Σ类型的题O(n^2)转化∑[n/i]∑[m/i],除法下结果相同的部分合并,复杂度降低至O(√n+√m)。当然论文里的题型应该说说很经典了。这里再积累几个基础题型。
1,求前n个正整数的约数之和,即∑=σ(i) ,(i=1到n)。其中n≤10^12。
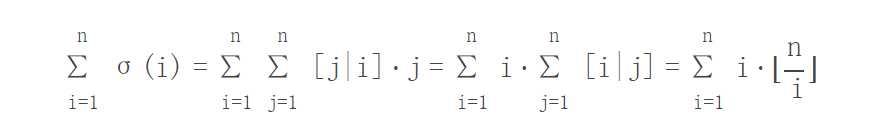
把除法下结果相同的部分合并,前面累加和用等差公式求和,复杂度为O(√n) 。
通俗理解公式: for(i=1;i<=n;i++) ans=ans+有因子i的数的个数=ans+n / i; (其中n/i=|i*1|+|i*2|+...+|i*(n/i)|,表示i是多少个数的因子)
例题: A New Function 。代码:

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<algorithm> #include<cstring> using namespace std; typedef long long ll; ll solve(int n) { ll ans=0; int B=sqrt(n); for(int i=2;i<=B;i++){ ans+=(ll)(n/i-1)*i; //前面根号n个直接暴力,由于不要1和本身,所以这里减一。 if(n/i>=B+1){ //后面合并商相同部分 ,L,R代表的是范围(个数)。 ll L=B+1,R=n/i; ans+=(L+R)*(R-L+1)/2; } } return ans; } int main() { int T,n,Case=0; scanf("%d",&T); while(T--){ scanf("%d",&n); printf("Case %d: %lld\n",++Case,solve(n)); } return 0; }
2,求前n个正整数的莫比乌斯函数之和,即∑=u(i),其中n≤10^11
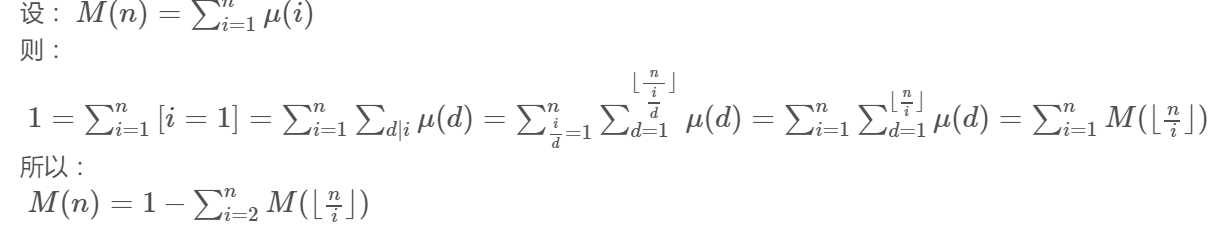
通俗理解公式:for(i=1;i<=n;i++) sum=sum+(u(1)+u(2)+u(3)+...u(j)) (其中,i*j<=n,表示以1到j为因子,i相同的合并)。
3,

