ng机器学习视频笔记（九）
——SVM理论基础
（转载请附上本文链接——linhxx）
一、概述
支持向量机（support vector machine，SVM），是一种分类算法，也是属于监督学习的一种。其原理和logistics回归很像，也是通过拟合出一个边界函数，来区分各个分类的结果。
二、代价函数与假设函数
由于svm和logistic很相似，故与logistic进行比较。logistic的代价函数如下：
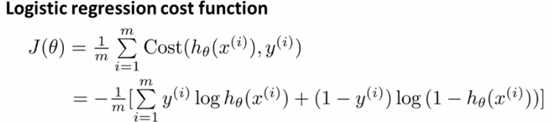
与logistic不同之处在于，SVM是用两个线段表示logistic中的h。在logistic中，h(x)=1/(1+e-z) (下图灰色部分)；在svm中，直接另h接近于0的地方等于0，而剩余的地方用一条线进行表示，如下图粉色部分所示：
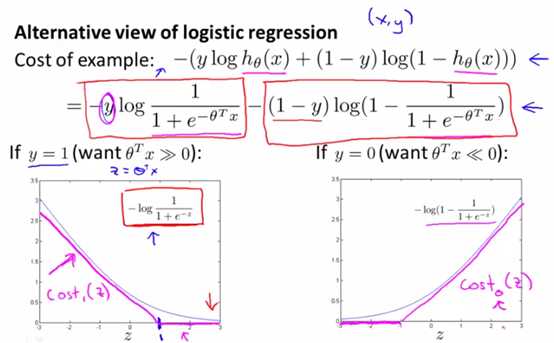
另外，svm的代价函数也省略了1/m，并且将原先logistic的正则化项λ提到前面，改成了C，可以认为C≈1/λ。
上图中的cost1和cost0，分别表示的是y=1和y=0的函数，因此，svm的假设函数如下所示：
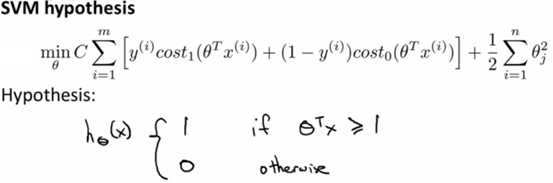
三、大间距分类器
1、概念
svm是一种大间距分类器（large margin intuition），即svm的算法得到的边界函数，会尽量的距离分类的不同结果都很远。
svm的决策边界如下：
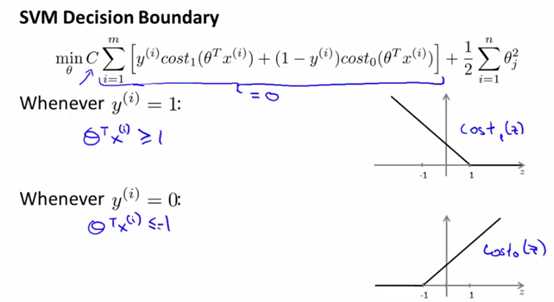
C很大，就要求[]中的那部分很小（令[]中的那部分表示为W），不如令其为0，这时来分析里面的式子：
y=1时，W只有前一项，令W=0，就要求Cost1(θTx)=0，由上图可知，这要求θTx>=1；
y=0时，W只有后一项，令W=0，就要求Cost0(θTx)=0，由上图可知，这要求θTx<=-1；
如下图所示，黑色那条会是svm拟合出来的边界函数，而不会是绿色或者粉色的线。其最大边界，指的就是其到两个分类结果中，最接近边界的点的垂直距离最大。
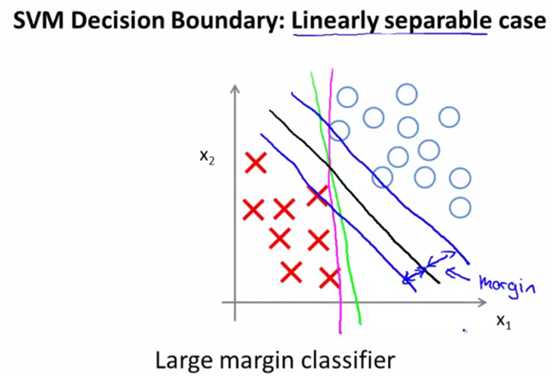
当上面代价函数中的C非常大时，svm的最大间距特性就会更明显。但是这样也会存在过拟合的问题，如下图所示：
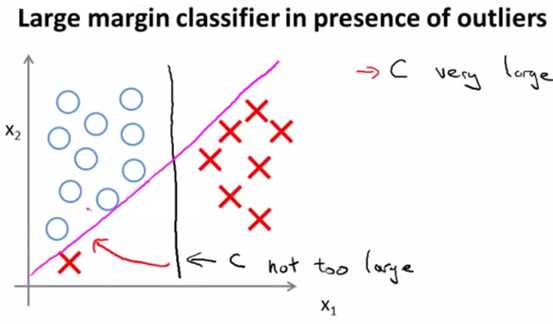
当分类存在一些误差的数据，则C太大时，算法会太过于纠结绝对意义上的最大距离，导致划分结果变成上图的粉色的线。C不太大时会是上图的黑色的线。
2、原理
1）
任意一点到面的距离如下：
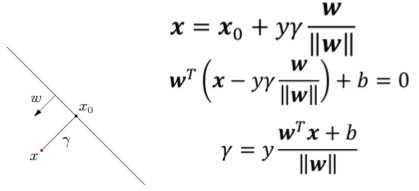
任意一个点x到分类平面的距离γ的表示如上图所示，其中y是{+1，-1}表示分类结果，x0是分类面上距x最短的点，分类平面的方程为wx+b=0,将x0带入该方程就有上面的结果了。对于一个数据集x，margin就是这个数据及所有点的margin中离hyperplane最近的距离，SVM的目的就是找到最大margin的hyperplane。
2）
两个向量内积的表现形式，假设向量u，v均为二维向量，我们知道u，v的内积uTv=u1v1+u2v2。表现在坐标上，如下图：
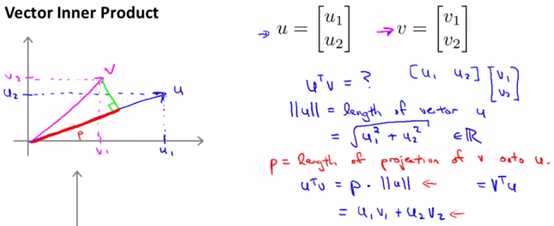
首先将v投影至u向量，记其长度为p（有正负，与u同向为正，反相为负，标量），则两向量的内积uTv = ||u||·||v||·cosθ = ||u||·p = u1v1+u2v2。
3）
svm能够自动的划分出最大边界，主要依据的是向量的点乘的原理。当C很大时，为了让代价函数尽量小，带C的那一项则需要为0，因此现考虑正则化项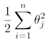
。正则化项可以换算成为欧式距离，即平方和带根号。
而要满足y=1，则需要θTx≥1，又θTx可以换算成向量的相乘模式，由于将C设的很大，cost function只剩下后面的那项。采取简化形式，意在说明问题即可，设θ0=0，只剩下θ1和θ2，则cost function J(θ)=1/2×||θ||^2，即如下图公式：
而根据上面的推导，有θTx=p·||θ||，其中p是x在θ上的投影，则：
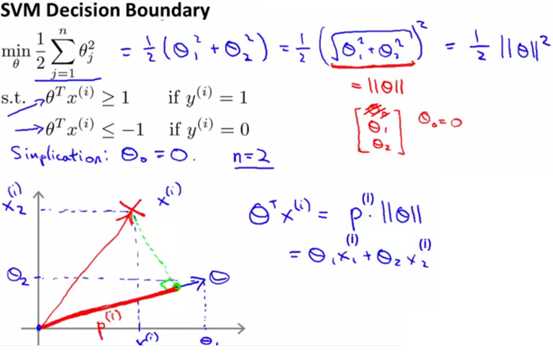
y=1时，W只有前一项，令W=0，就要求Cost1(θTx)=0，由右图可知，这要求p·||θ||>=1；
y=0时，W只有后一项，令W=0，就要求Cost0(θTx)=0，由右图可知，这要求p·||θ||<=-1。如下图所示：
因此，当预测点在y=1的时候，其要求θTx≥1，也即要求P||θ||≥1，而这个公式中，P向量是每个点到边界函数的投影，因此如果边界函数不合理的情况下，点到边界函数的投影值会很小，要实现乘积≥1，则需要θ非常大，也就会使得代价函数的结果非常大。
则在优化代价函数的过程中，慢慢的就会调整出一个合适的θ。如下图所示，下图左边即为不符合的边界函数，右边是符合的边界函数：
四、核函数
1、高斯核函数
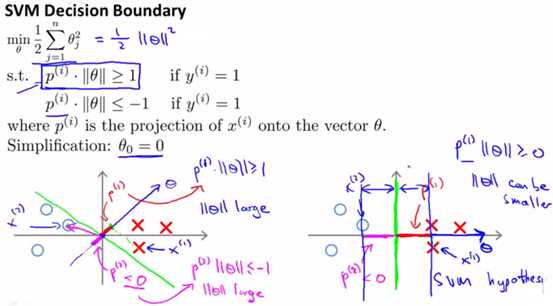
svm的分类，除了可以用上面的线性的分类器（也成为线性核函数），还可以用到其他的核函数（kernel）。所谓核函数，也就是帮助svm实现分类的边界函数。
最常用的非线性的核函数即高斯核函数（Gaussian kernel）。其主要公式即为高斯分布的公式。可知当x很接近l时，结果是1；x远大于（或远小于）l时，结果是0。
高斯核函数，可以写为f=similarity(x,l)，另外所有的核函数都可以写为k(x,l)。
如下图所示：
利用高斯核函数，可以非线性的划分边界函数。例如样本的分类是几个同心圆的范围，则此时线性划分无法解决问题，就需要用到高斯核函数来划分。
2、性质
δ值会影响到高斯核函数的划分结果。下图是不同的δ值对应的三维图像，以及其等价线图。可以看出，δ值越大，则核函数越平缓，即0和1的区间分布的中越偏向于1；而δ值越小，则0所占的比例越大，其图像越尖。
原因在于公式，从公式上可以看出，δ值越小，越趋向于e的负无穷大次方，即为0；反之则越趋向于e的0次方，即为1。
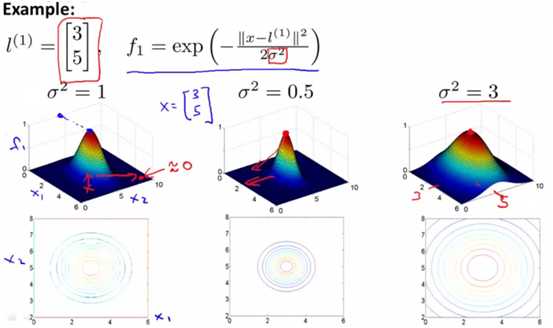
五、高斯核函数实际判定过程
假设样本l(1)，则其对应的x1和x2已经固定，则带入到原来拟合好的边界函数中，可以得到对应的点f的值。并用之前拟合出来的θ值，计算最终的结果，结果如果≥0则表示y=1，反之y=0。如下图所示：
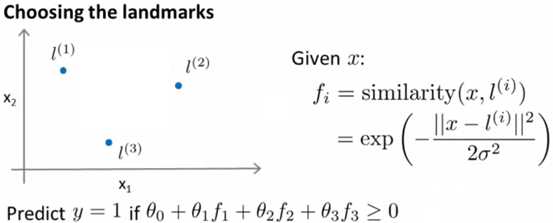
具体过程，即一开始给定了若干样本，带有特征值矩阵x、分类结果y，令l=x，则可以求解出对应的f矩阵，进而求解出上面的θf是否≥0。这里与之前讲过的cost function的区别在于用kernel f 代替了x。
在SVM的训练中，将Gaussian Kernel带入cost function,通过最小化该函数就可与得到参数θ，并根据该参数θ进行预测：若θTf>=0，predicty=1；else predict y=0。
另外，在实际的代码中，通常计算正则化项（即θ平方和项），虽然平方和等价于θTθ，但是不会直接这么计算，因为当特征值特别多时，这样计算的量太大。有一个叫做SMO的算法，可以快速进行计算。
六、小结
1、拟合问题
这里主要有C（即1/λ）和δ两个参数。
C的性质类似1/λ的性质，可以参照logistic，当C太大时容易出现高方差过拟合，C太小时容易出现高偏差欠拟合。
δ的性质上面提到过，和正态分布中的定义一样，太大容易高偏差欠拟合，且变化缓慢；太小容易出现高方差过拟合，且变化太快。
2、归一化
如果用到高斯核函数，当特征值之间的数量值差距太大，需要将特征值归一化。
3、默塞尔定理
默塞尔定理（Mercer’s theorem），是对核函数的一个规定。即要求核函数能满足优化方法，且要能快速得到θ。
选择svm的核函数时，要求选择的核函数都要满足默塞尔定理。
4、其他核函数介绍
svm最常用的核函数还是线性核函数和高斯核函数。除此之外还有其他不常用的核函数：
1）多项式核函数（polynomial kernel）
k(x,l)=(xTl+C)m，C是常数，m是次数。有个性质是当x和l很接近时，k的值会非常大。用这个多项式，通常要求样本的特征值都是大于0的。
2）字符串核函数（string kernel）
当涉及到文本处理的时候，通常用到这个核函数。
3）其他
还有诸如卡方核函数（chi-square kernel）、直方相交核函数（histogram intersection kernel）等复杂的核函数。
5、选择logistic或者svm
1）特征很多、样本很少
此时需要用logistic或者svm的线性核函数，避免过拟合。
2）特征少、样本正常
此时使用svm的高斯核函数非常合适。
3）特征少、样本非常多
此时也不适用高斯核函数，因为其计算量太大，速度太慢。通常是先增加或者创造部分特征，再使用logistic或者svm的线性核函数。
6、个人感悟
svm的方程比较复杂，吴恩达的视频中并没有完整的讲述推导过程，个人感觉，svm是一个非常类似logistic的分类方式，区别在于可以最大程度上区分两个分类结果，并且可以通过不同的核函数控制分类方式，可以非线性分类。
——written by linhxx
更多最新文章，欢迎关注微信公众号“决胜机器学习”，或扫描右边二维码。
