1.引出递归函数
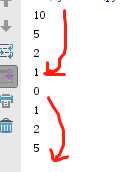
- 需求:把10不断除以2,知道不能除为止
n = 10 while True: n = int(n/2) print(n) if n == 0: break # 结果 5 2 1 0
2.递归深度
(1)递归深度
def cacl(n): print(n) return cacl(n/2) cacl(10)
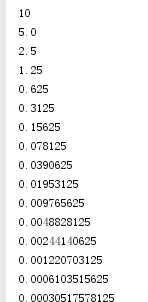

(2)查看递归深度

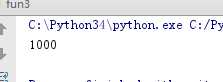
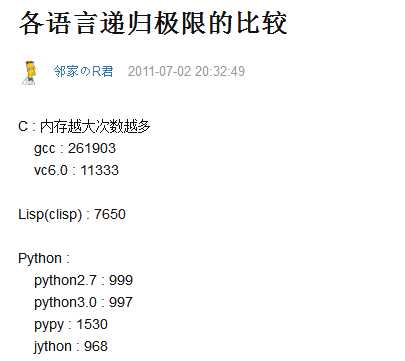
(3)递归函数
def cacl(n): print(n) n = int(n/2) if n > 0: # 递归出口 cacl(n) cacl(10) # 结果 10 5 2 1
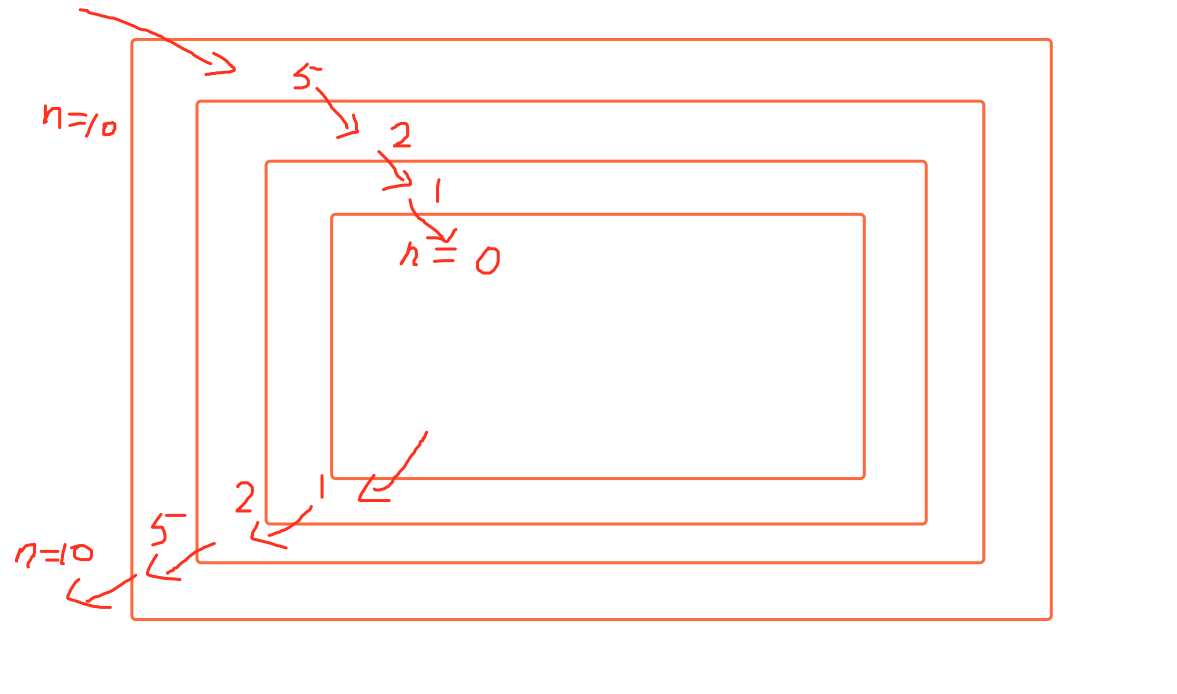
3.递归函数如何递归?
- 一层层进去
- 一层层出来

4.练习
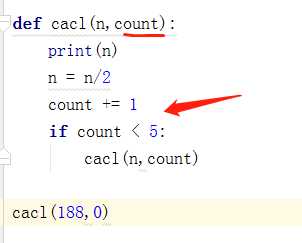
(1) 只除以5次,
(2)只打印第5次的值
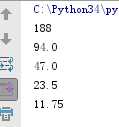
def cacl(n,count): print(n,count) if count < 5: return cacl(n/2,count+1) else: return n val = cacl(188,1) print(val) # 结果 188 1 94.0 2 47.0 3 23.5 4 11.75 5 11.75
3.递归特性
-
必须有一个明确的结束条件
-
每次进入更深一层递归时,问题规模相比上次递归都应有所减少
-
递归效率不高,递归层次过多会导致栈溢出(在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出)
堆栈扫盲http://www.cnblogs.com/lln7777/archive/2012/03/14/2396164.html
4.递归实际案例
(1)二分查找
data = [1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35] def binary_search(dataset,find_num): print(dataset) if len(dataset) >1: mid = int(len(dataset)/2) if dataset[mid] == find_num: #find it print("找到数字",dataset[mid]) elif dataset[mid] > find_num :# 找的数在mid左面 print("\033[31;1m找的数在mid[%s]左面\033[0m" % dataset[mid]) return binary_search(dataset[0:mid], find_num) else:# 找的数在mid右面 print("\033[32;1m找的数在mid[%s]右面\033[0m" % dataset[mid]) return binary_search(dataset[mid+1:],find_num) else: if dataset[0] == find_num: #find it print("找到数字啦",dataset[0]) else: print("没的分了,要找的数字[%s]不在列表里" % find_num)
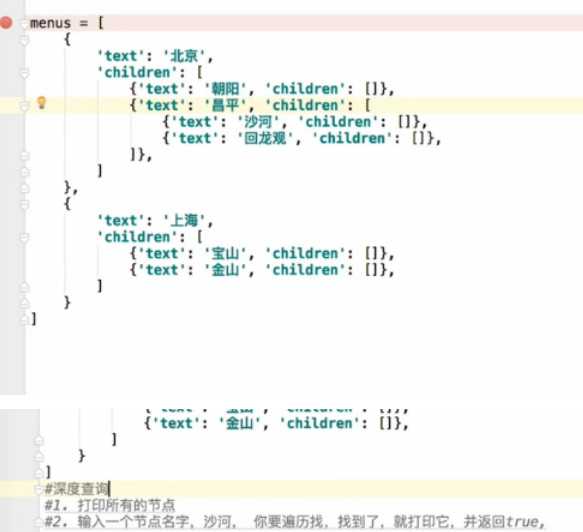
(2)深度查询