ng机器学习视频笔记(十三)
——异常检测与高斯密度估计
(转载请附上本文链接——linhxx)
一、概述
异常检测(anomaly detection),主要用于检查对于某些场景下,是否存在异常内容、异常操作、异常状态等。异常检测,用到了一个密度估计算法(density estimation)——高斯分布(Gaussian distribution),又称正态分布(normal distribution)。
该算法只用到了样本的特征值,不需要分类标签,故该算法是无监督学习算法
主要内容是,对于样本集,当有一个新的数据,用计算这个数据的概率,并判断其是否小于ε。对于概率小于ε的,判定为异常数据;反之为正常数据。下图绿色的点即为异常数据,如下图:
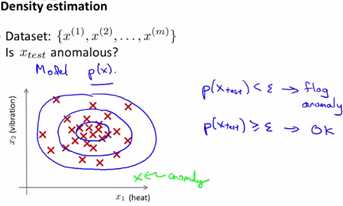
二、高斯分布
高斯分布,即概率论的知识,其主要用均值μ、方差δ2来表示,如下图所示:
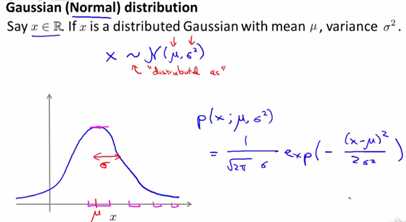
其中,μ和δ对于每个特征,都有一个特定的值,其是所有样本对于该特征值的均值和方差。
当改变μ、δ时,概率分布图会有所变化。δ变小会让图变尖,反之变扁;μ变小图像会左移,反之右移。如下图所示:
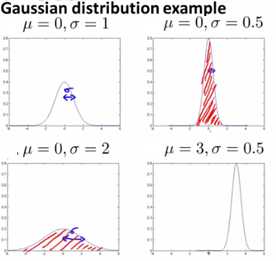
三、异常检测算法
步骤如下:
1、选取参与概率计算的特征值,必要时进行处理(选取和处理方式下文会提到)。
2、对于每个特征值,计算μ、δ,进而计算出每个特征值的概率公式pj(x)。
3、将所有参与计算的特征值的概率公式相乘,得到总的概率公式p(x)。注意,这里有个前提,是这些特征互相之间不想关,即互相独立。这种计算方式,称为极大似然估计(maximum likelihood estimation),也是概率论中的一种计算概率的方式。
4、对于一个给定的样本x,计算p(x),如果p(x)<ε,则认为这个异常;否则正常。ε是一个比较小的数字,如0.02等,下面会提到如何选ε。
过程如下图所示:

四、评价异常检测算法
异常检测算法的评价,不能直接算正确率。这是因为考虑到使用场景,通常正常的数据量非常大,而异常的数据量极少。因此,这里需要用到之前提到的查准率、召回率,进而计算F1的值,来评价算法。
回顾这块的内容:
F1=2PR/(P+R),其中P表示查准率,R表示召回率,F1的值越大表示模型越好。关于P、R、F1,这里直接截取我之前文章的部分内容,详见 ng机器学习视频笔记(八) ——机器学习系统调试(cv、查准率与召回率等)

对于样本,假设有10000个正确的样本,20个错误的样本,这里需要设计训练集、交叉验证集、测试集,则:
训练集使用6000的正确样本(训练集不用错误样本,因此训练集也不需要用到输入的样本分类结果标签y),CV集和test集各使用2000正确样本和10个错误样本进行验证(通过对照输出结果和原始的标签y)。
对于选择ε,可以通过几个不同的ε,运用交叉验证,看哪个ε最终计算出来的F1最大,则使用那个ε。
评价过程如下:

五、异常检测和监督学习区别
上面的异常检测算法的过程,也用到了分类结果y进行验证,而且实际上输入的样本也有分类标签,只不过不使用而已。而且在CV、test阶段都用到了分类结果。因此异常检测和监督学习算法有些相似性,但是这里有所区别。
最主要还是从业务场景角度出发,异常检测主要的目的在于检测出输入是否有异常,因此其通常样本中异常的数据非常少,而且异常的种类可能会非常多,甚至有可能会出现全新的异常情况。
对于监督学习,通常分类为正、负的样本数量差不多,而且新的数据过来时,很少会出现完全没有出现过的情况。
因此,根据不同的业务场景,就可以区分是需要使用异常检测算法还是监督学习算法。如下图所示:

就异常检测和监督学习的区别而言,错误检测主要用于欺骗检测、工业检测、数据中心设备检测等,监督学习则主要用于垃圾邮件分类、天气预测、疾病诊断等(实际上监督学习还有非常多的应用场景)。
六、高斯分布参数选择
对于高斯分布模型,需要确定样本的哪些特征参与计算,且如果特征的数据不满足,还需要进行适当的变换特征。
1、特征自身变换
当特征的分布不是高斯分布时,则通常需要给特征加上一些函数的变换,让其图像变为高斯分布,例如可以使用log(x)、x的幂次等代替x,来使得图像变成高斯分布,如下图所示:
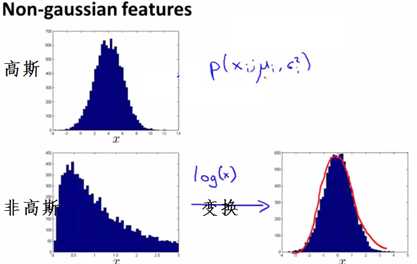
2、特征数量不足
对于高斯分布,我们希望正常结果时的p(x)值尽量大,而异常时尽量小,以便于区分。如果某个特征,其异常值时不够小,则可以考虑再引入一个特征,让高斯分布从变成二维的分布图像,进而解决这个问题,如下图所示:
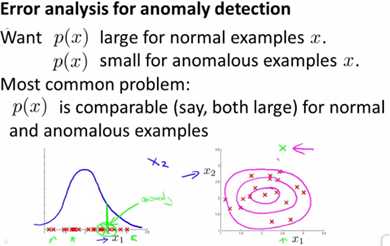
3、特征的综合处理
考虑一个业务场景:检测数据中心的计算机的CPU使用率和网络使用率。这两者通常是都非常大的,因此单独检测这两个特征,他们的变化不够敏感。
假设CPU特征为x1,网络特征为x2,可以考虑使用人造一个新特征x3=x1/x2,则此时如果cpu异常大或网络异常小,则x3的值会明显增大;反之x3会明显减小。
更进一步,如果特别关注的是CPU的使用情况,可以令x3=x12/x2,给x1加了平方后,其变化反应在图像上就更为明显。
七、多元高斯分布
1、一元高斯分布局限性
回顾一元高斯分布,计算概率p(x),是把每个特征的pj(x)相乘得到的,这里有个前提是每个特征之间独立。当特征之间存在相关性,不符合相关性也表示数据异常,则一元高斯分布无法满足要求。
看下图,CPU使用率和内存使用率大体上是一个正向关系,当出现内存非常高而cpu很低时,实际上是异常的,但是两个一元高斯计算出来都未必是异常,如下图所示。下图左图中,蓝色的弧线才是真正的正常范围,而一元高斯会将粉色区域都当作正常范围。
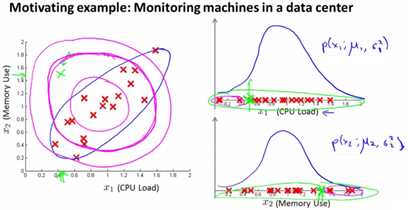
2、多元高斯分布公式
考虑到特征之间的关联,则需要引入多元高斯分布(Multivariate Gaussian Distribution),其认为特征之间存在相关性的可能,计算公式有所改变,可以满足上述要求。公式如下图所示:
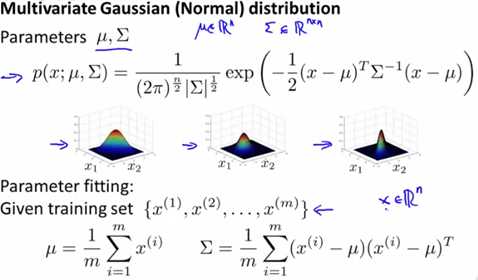
这里的μ变成n维向量,Σ是一个n*n矩阵,|Σ|是计算Σ的行列式,同理Σ-1是计算Σ的逆矩阵。
3、多元高斯图像特性
考虑二维的情况。
1)标准情况
把下图最左边的那张图当作标准情况,即μ是2维0向量,Σ是2阶单位矩阵。此时,图像在(0,0)点取得最大值,且关于x1、x2轴对称。
2)Σ是对角阵且倍乘
当Σ倍乘,如果值小于1,则图像变尖,大于1则变扁。如下图的中、右两幅图所示。
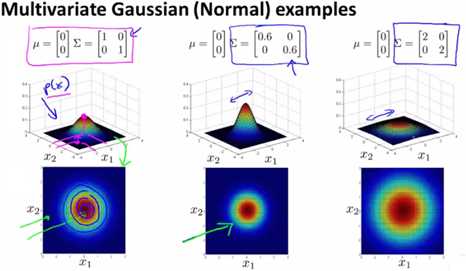
3)Σ是对角阵且非倍乘
被乘的那个维度,如果乘完后小于1则那个维度上变尖,反之那个维度变扁。下图中间和右边的图,分别是第一维小于1、大于1,相应的变尖、变扁。
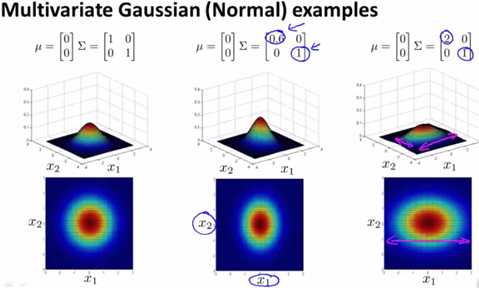
4)Σ非对角阵-倍加
如果非对角阵方向加上正数,则往右倾斜,且值越大倾斜越明显。下图即类似上面分析CPU和内存的业务场景锁钥用到的二元高斯分布。
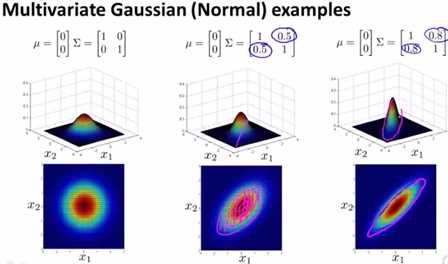
5)Σ非对角阵-倍减
如果非对角阵方向加上负数,则往左倾斜,且值越大倾斜越明显。
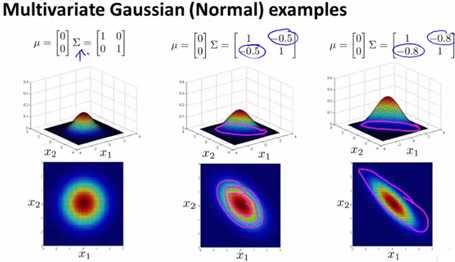
6)μ的变化
μ是均值,因此μ的变化会导致图像平移,哪个维度变了则在那个维度上进行平移,比较简单不展示图片。
八、对照一元和多元高斯分布
1、相似
实际上,当多元高斯分布的Σ,是一个对角矩阵,且每个δ2都是对应特征值的δ2时,则多元高斯分布模型完全等同于一元高斯分布模型。可以把一元高斯分布模型理解成一种特殊的多元高斯分布模型。
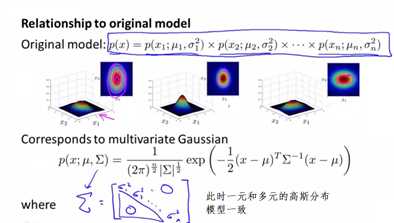
2、使用场景
1)多元高斯分布优点
根据上面的分析,多元高斯分布是一种通用的场景,其必然有比一元高斯分布更灵活的特点。
2)多元高斯分布缺点
其存在局限性:多元高斯分布要求样本数量m要多于参与计算的特征数量n,且通常需要m≥10n时,效果才比较好。另外,多元高斯分布还需要计算Σ的逆矩阵,因此这里还要求Σ可逆,且求逆矩阵是一个非常大计算量的工作,因此特征非常多时,使用多元高斯分布计算速度会比较慢。
3)一元高斯分布优点
一元高斯分布,其速度快、计算量小,且不要求样本数量比特征数量多。当需要特殊的特征监控,也可以用到上面提到的人造一个特征的方式来弥补少量的特征非独立情况。
4)一元高斯分布缺点
很明显,当大量的特征非独立,需要人造特征,是一元高斯分布的缺点。

九、总结
高斯分布的错误检测方式,是一种基于概率的思想的错误检测。我学到这个的时候,首先想到的是一个故事:一个渔夫在激流上划船,激流上很多暗礁,但是他从来都很安全。有人问他怎么躲过那么多的暗礁,他的回答是:“我不知道哪些地方有暗礁,我只知道哪条路是可以走的。”
对于高斯分布检测,完全就是基于这个思想。因此样本的训练也只给正确数据去训练,学习的时候也只学习正确的情况,所有非正确情况,都被当作大概率上是异常情况来处理,对于需要多大的概率,则用到ε来控制。
这种思想,对于快速揪出错误,具有重要意义。
——written by linhxx
更多最新文章,欢迎关注微信公众号“决胜机器学习”,或扫描右边二维码。
