由于这是第一天去实现polya题,所以由易到难,先来个铺垫题(假设读者是看过课件的,不然可能会对有些“显然”的地方会看不懂):
1,n比较小,恶意的揣测出题人很有可能出超级多组数据,所以先打表。
2,考虑旋转:
for(i=0;i<n;i++) sum+=pow(n,gcd(n,i));
3,考虑翻转:
if(n&1) sum+=n*pow(3,n/2+1) ;
else {
sum+=n/2*pow(3,n/2) ;
sum+=n/2*pow(3,n/2+1) ;
}
4,除以总置换数(n+n/2+n/2):
5,终极代码:


#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;
#define ll long long
ll ans[30];
ll gcd(ll a,ll b) { if(b==0) return a; return gcd(b,a%b); }
ll pow(ll a,ll x)
{
ll res=1;
while(x){
if(x&1) res*=a;
x>>=1;
a*=a;
} return res;
}
int main()
{
ll n,i,sum;
for(n=1;n<=23;n++){
sum=0;
for(i=0;i<n;i++) sum+=pow(3,gcd(n,i));
if(n&1) sum+=n*pow(3,n/2+1) ;
else {
sum+=n/2*pow(3,n/2) ;
sum+=n/2*pow(3,n/2+1) ;
}
ans[n]=sum/n/2;
}
while(~scanf("%lld",&n)){
if(n==-1) return 0;
printf("%lld\n",ans[n]);
}
return 0;
}
View Code
----------------------------------------------------分界线--------------------------------------------------------------------------------
POJ2154 Color: 求可以旋转,不可以翻转的置换,n个珠子,n种颜色,答案mod K,n<1e9。
那么本题只考虑旋转,则:
for(i=0;i<n;i++) ans+=pow(n,gcd(n,i));
ans/=n;
之前莫比乌斯那里,我们常用技巧是合并。 这里考虑gcd相同的合并。(做多了还是有点灵感滴,yeah)。
得到: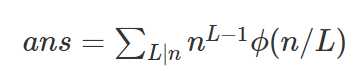
解决这个公式需要:快速幂+欧拉公式+一些素数的常识。
1,快速幂不说了,注意先模运算。
2,欧拉公式,枚举L,即n的素因子,然后根据phi=L*(1-1/p1)*(1-1/p2)...得到欧拉函数。
3,素数常识,在这里指的是一个数n的素因子最多有一个大于根号n,所以一直除,把根号n前的素数都除完了,留下的一定是大于根号n的一个素数。
//可以线筛一部分欧拉函数出来,不够的再枚举素数;枚举的话不超过根号个,所以复杂度不会太高。
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=100000;
int ans, Mod;
int pri[maxn+10],cnt,vis[maxn+10],phi[maxn+10];
int qpow(int a,int x)
{
int res=1;a%=Mod;//这里a一定要除一下,不然会超int,猪啊。
while(x){
if(x&1) res=res*a%Mod;
x>>=1; a=a*a%Mod;
} return res%Mod;
}
void prime()
{
phi[1]=1;
for(int i=2;i<=maxn;i++){
if(!vis[i]) pri[++cnt]=i,phi[i]=i-1;
for(int j=1;j<=cnt&&pri[j]*i<=maxn;j++) {
vis[pri[j]*i]=1;
if(i%pri[j]==0) {
phi[i*pri[j]]=phi[i]*pri[j];
break;
}
else phi[i*pri[j]]=phi[i]*(pri[j]-1);
}
}
}
int Phi(int x)
{
if(x<=maxn) return phi[x]%Mod;
int res=x;
for(int i=1;pri[i]*pri[i]<=x;i++)
if(x%pri[i]==0){
res=(res-res/pri[i]);
while(x%pri[i]==0) x/=pri[i];
}
if(x!=1) res=(res-res/x);
return res%Mod;
}
int main()
{
int n,T; prime();
scanf("%d",&T);
while(T--){
ans=0; scanf("%d%d",&n,&Mod);
for(int i=1;i*i<=n;i++){
if(n%i!=0) continue;
ans=(ans+qpow(n,i-1)*Phi(n/i))%Mod;
if(i*i!=n) ans=(ans+qpow(n,n/i-1)*Phi(i))%Mod;
}
printf("%d\n",ans);
} return 0;
}