Description
问题的描述以及输入输出的样例可以看这里:链接
思路
虽然 DISCUSS 中总有人说水题,但是我觉得这道题的质量可以 (或许我比较弱ORZ ,在做过的 DP 题里算 medium 难度。
题目的意思是给你一个主串和一堆子串,需要你将子串和主串完全匹配上,在匹配过程中可以删除主串中匹配不上的字符,最后统计出被删除的最少字符数目。
比如主串是 carmsr ,子串有 car 、mr 两种。可以只用 car 去匹配,那么匹配不上的字符有 m、s、r 三个,所以需要删除三个字符;可以用 car、mr 去匹配,那么匹配不上的字符有 s 一个,所以需要删除一个字符。那么在个样例里最终的输出就是 1。
枚举算法的时间复杂度是指数阶,直接出局,决定从后往前简单搜索。在过程中发现这道题是具有最优子结构的,即问题的最优解是由子问题的最优解演变而来的,当前位置最少删除字符数目与之前位置的最少删除字符数目有直接关系,即当前位置没有被匹配上的话,那么当前位置的最少删除字符数目就是前一个位置的最少删除字符数目加一;如果匹配上的话,演变关系比较饶一点,还是通过例子说明吧:
//主串 browndcodw,子串 cow browndcodw co w l r //当前位置位于末尾的 w ,子串 cow 匹配到的位置如图所示
//那么,当前位置的删除字符数目 = r - l +1 - 3 + 前6个字符的最小删除字符数目
通过这个例子还可以发现,原问题还有很多公共的子问题,若此时再给一个子串 cod 进行匹配,那么两个子串匹配后主串中剩下的子串的长度是一致的,它们的子子问题其实是同一个问题。
我们定原问题为状态,即状态为前 i 个字符需要删除的字符数,设为 dp[i] ,那么可以推出状态转移方程:
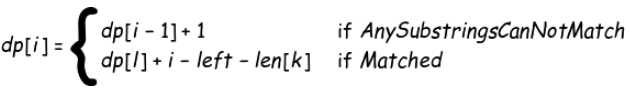
有了方程,写算法就容易多了。算法使用采用迭代实现,时间复杂度为 O(W·L^2)

#include<iostream> #include<vector> #include<string> using namespace std; #define INT_MAX 600000 const int MAX_WORD_NUM = 600; const int MAX_MES_LENGTH = 300; int dp[MAX_MES_LENGTH + 1]; int len[MAX_WORD_NUM + 1]; string dir[MAX_WORD_NUM + 1]; int main(void) { int word_num, mes_length; string mes; cin >> word_num >> mes_length; cin >> mes; //int dp[mes_length+1]; //int len[word_num+1]; dp[0] = 0; for (int i = 1; i <= mes_length; ++i) { dp[i] = INT_MAX; } //string dir[word_num+1]; for (int i = 1; i <= word_num; i++) { cin >> dir[i]; len[i] = dir[i].size(); } for (int i = 1; i <= mes_length; ++i) { bool match_flag = false; for (int k = 1; k <= word_num; k++) { int l = i-1, r = i-1; //从后往前匹配 int j; for (j = len[k]-1; l >= 0; ) { if (dir[k][j] == mes[l]) { j--; if (j == -1) //单词匹配成功,l无需再左移 break; } else if (dir[k][j] != mes[l] && j == len[k]-1) { r--; } l--; } //*cout << "现在是第 " << k << "个单词在进行匹配! " <<"l is :" << l << " " << "r is :" << r << endl; //主串匹配上了当前单词 if (j == -1) { //dp为含前i个字符的主串需要删去的字符总数 dp[i] = std::min(dp[i], dp[l] + i - l - len[k] ); //dp[l] + (i-1) - l - len[k] match_flag = true; } } //mes的前i个字符都没有匹配上任何单词 if (match_flag == false) { dp[i] = dp[i-1] + 1; } } cout << dp[mes_length] << endl; return 0; }

