神经网络的激活函数及梯度消失

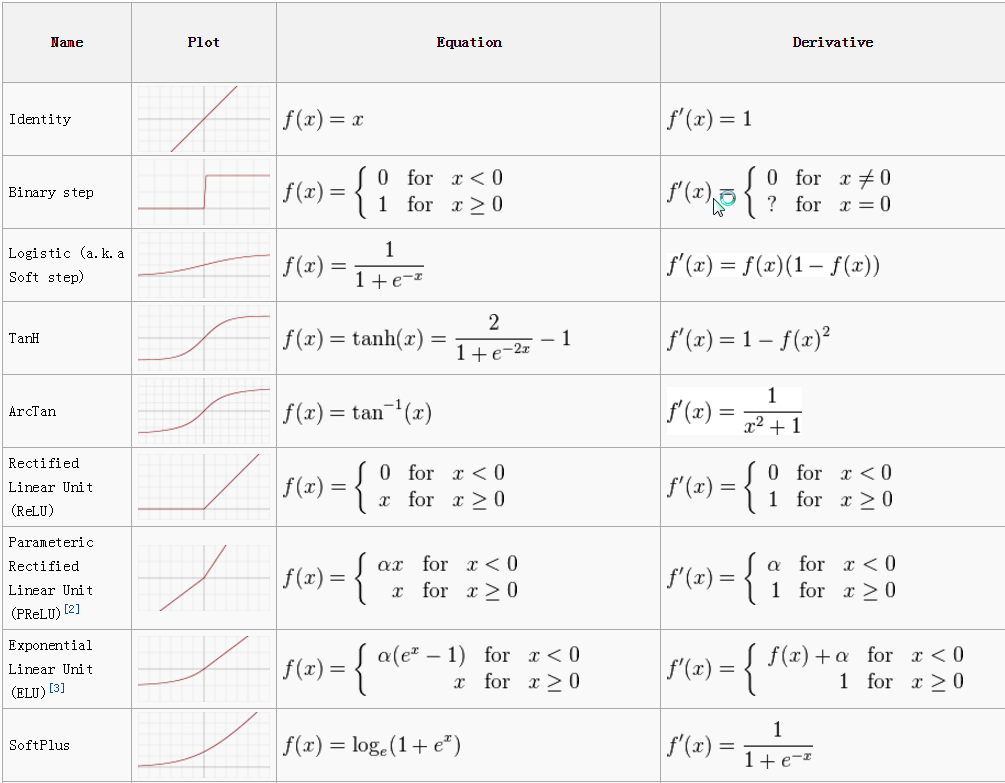
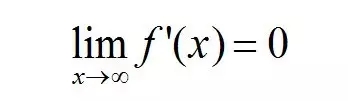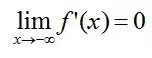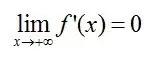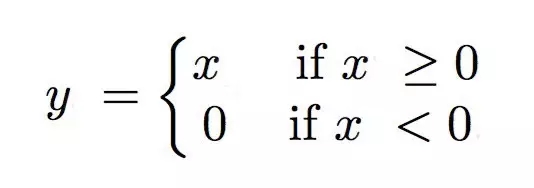   ICML 2016 的文章[Noisy Activation Functions]中给出了激活函数的定义：激活函数是映射 h:R→R，且几乎处处可导。

   神经网络中激活函数的主要作用是提供网络的非线性建模能力，如不特别说明，激活函数一般而言是非线性函数。假设一个示例神经网络中仅包含线性卷积和全连接运算，那么该网络仅能够表达线性映射，即便增加网络的深度也依旧还是线性映射，难以有效建模实际环境中非线性分布的数据。加入（非线性）激活函数之后，深度神经网络才具备了分层的非线性映射学习能力。

1、Sigmoid函数

     Sigmoid 是使用范围最广的一类激活函数，具有指数函数形状 。正式定义为：

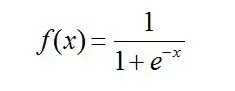
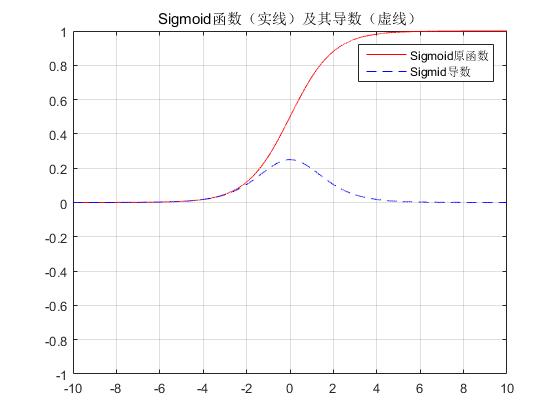
x=-10:0.001:10; 
%sigmoid和它的导数
sigmoid=1./(1+exp(-x));
sigmoidDer=exp(-x)./((1+exp(-x)).^2);
figure;
plot(x,sigmoid,‘r‘,x,sigmoidDer,‘b--‘);
axis([-10 10 -1 1]);
grid on;
title(‘Sigmoid函数（实线）及其导数（虚线）‘);
legend(‘Sigmoid原函数‘,‘Sigmid导数‘);
set(gcf,‘NumberTitle‘,‘off‘);
set(gcf,‘Name‘,‘Sigmoid函数（实线）及其导数（虚线）‘);

输出：

   可见，sigmoid 在定义域内处处可导，且两侧导数逐渐趋近于0，即：

    Bengio 教授等将具有这类性质的激活函数定义为软饱和激活函数。与极限的定义类似，饱和也分为左侧软饱和与右侧软饱和：

左侧软饱和：

右侧软饱和：

    与软饱和相对的是硬饱和激活函数，即：f‘(x)=0，当 |x| > c，其中 c 为常数。

    同理，硬饱和也分为左侧硬饱和和右侧硬饱和。常见的ReLU 就是一类左侧硬饱和激活函数。

Sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。具体来说，由于在后向传递过程中，sigmoid向下传导的梯度包含了一个f‘(x) 因子（sigmoid关于输入的导数），因此一旦输入落入饱和区，f‘(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象[Understanding the difficulty of training deep feedforward neural networks]。梯度消失问题至今仍然存在，但被新的优化方法有效缓解了，例如DBN中的分层预训练，Batch Normalization的逐层归一化，Xavier和MSRA权重初始化等代表性技术。

    Sigmoid 的饱和性虽然会导致梯度消失，但也有其有利的一面。例如它在物理意义上最为接近生物神经元。(0, 1) 的输出还可以被表示作概率，或用于输入的归一化，代表性的如Sigmoid交叉熵损失函数

2、tanh函数

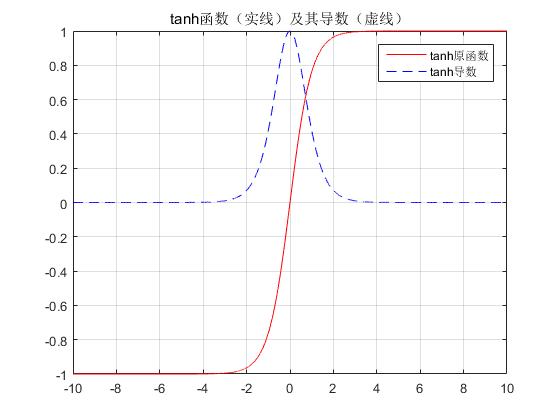
x=-10:0.001:10;
tanh=(exp(x)-exp(-x))./(exp(x)+exp(-x));
tanhDer=1-tanh.^2;
figure;
plot(x,tanh,‘r‘,x,tanhDer,‘b--‘);
grid on;
title(‘tanh函数（实线）及其导数（虚线）‘);
legend(‘tanh原函数‘,‘tanh导数‘);
set(gcf,‘NumberTitle‘,‘off‘);
set(gcf,‘Name‘,‘tanh函数（实线）及其导数（虚线）‘);

输出：

    tanh也具有软饱和性。[Backpropagation applied to handwritten zip code recognition]中提到tanh网络的收敛速度要比sigmoid快。因为tanh的输出均值比sigmoid更接近0，SGD会更接近 natural gradient[Natural gradient works efficiently in learning]（一种二次优化技术），从而降低所需的迭代次数。

3、Softsign函数

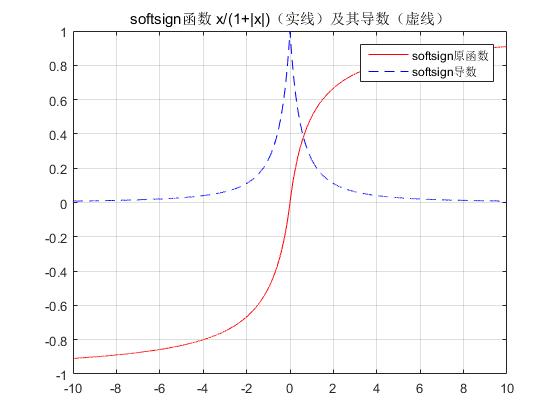
x=-10:0.001:10;
softsign=x./(1+abs(x));
%分段函数的表示方法如下
%y=sqrt(x).*(x>=0&x<4)+2*(x>=4&x<6)+(5-x/2).*(x>=6&x<8)+1*(x>=8);
softsignDer=(1./(1+x).^2).*(x>=0)+(1./(1-x).^2).*(x<0);
plot(x,softsign,‘r‘,x,softsignDer,‘b--‘);
axis([-10 10 -1 1]);%加在第一个plot后面
grid on;
title(‘softsign函数 x/(1+|x|)（实线）及其导数（虚线）‘);
legend(‘softsign原函数‘,‘softsign导数‘);
set(gcf,‘NumberTitle‘,‘off‘);
set(gcf,‘Name‘,‘softsign函数 x/(1+|x|)（实线）及其导数（虚线）‘);

输出：

4、RELU

定义为：

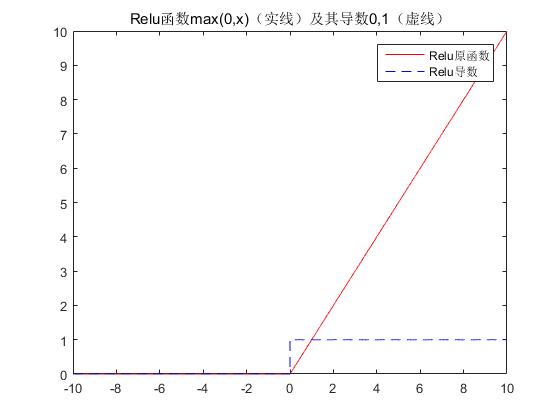
x=-10:0.001:10;
relu=max(0,x);
%分段函数的表示方法如下
%y=sqrt(x).*(x>=0&x<4)+2*(x>=4&x<6)+(5-x/2).*(x>=6&x<8)+1*(x>=8);
reluDer=0.*(x<0)+1.*(x>=0);
figure;
plot(x,relu,‘r‘,x,reluDer,‘b--‘);
title(‘Relu函数max(0,x)（实线）及其导数0,1（虚线）‘);
legend(‘Relu原函数‘,‘Relu导数‘);
set(gcf,‘NumberTitle‘,‘off‘);
set(gcf,‘Name‘,‘Relu函数（实线）及其导数（虚线）‘);

输出：

     可见，ReLU 在x<0 时硬饱和。由于 x>0时导数为 1，所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。但随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为“神经元死亡”。

     ReLU还经常被“诟病”的一个问题是输出具有偏移现象[7]，即输出均值恒大于零。偏移现象和 神经元死亡会共同影响网络的收敛性。

    还有其他一些激活函数，如下表：

http://blog.csdn.net/cyh_24/article/details/50593400

http://blog.51cto.com/qing0991/1833398