字典树,顾名思义,是用来进行字符串查找的一种数据结构。试想一下,如果给你一堆字符串,问你其中每个字符串是否出现过,那怎么办?很容易,map,短小精悍。那如果给你一堆单词,再丢给你另一堆字符串,问你字符串中出现过哪些单词构成的前缀呢?
这里就可以用到trie树这种结构了。
首先假设所有字符串均为小写,给你以下几个单词:
cat,cash,app,apple,aply,ok
那么可以构成下面这样一个trie树:
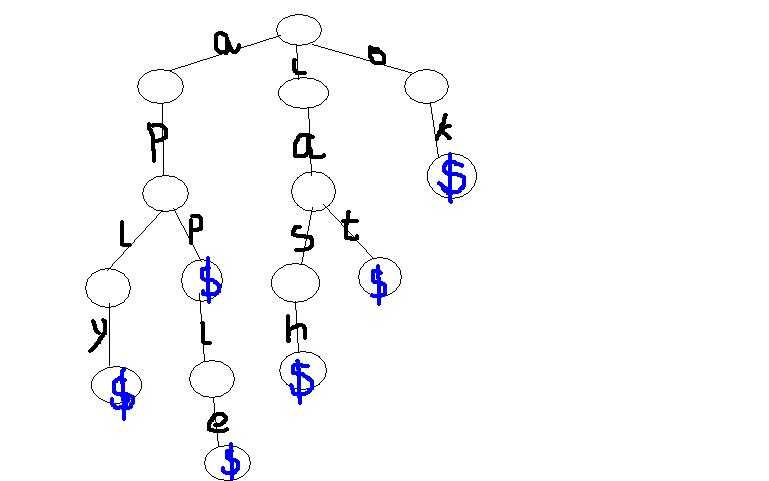
因此可得出:
1,字典树用边表示字符(其实也可以用点表示)
2,前缀相同的单词共用前缀结点,因此一个结点最多有26个子节点
3,根节点为空,这样是为了方便查找,后面会讲
4,一个单词结束后用一个特殊字符表示结束(用结构体的话也可以放一个bool变量),根节点到每一个标记就表示一个单词
那么下面讲讲trie树的基本操作:
1,插入insert
很简单,从根节点开始遍历,如果有相同的前缀,那就直接沿着前缀向下继续遍历;如果找不到相同前缀,就插入新的字符,一直到单词结束。
那既然如此就涉及到结点的编号,trie树中每个结点都有两种编号,一种是按插入顺序编号,另一种是按字母编号,下图中,红色标号是第一种,紫色是第二种,可以看出,按第一种编号的话,相同字母可能有不同的编号,按第二种编号,相同字母的标号相同,并只有26种,用s表示该字符,即s-‘a‘;
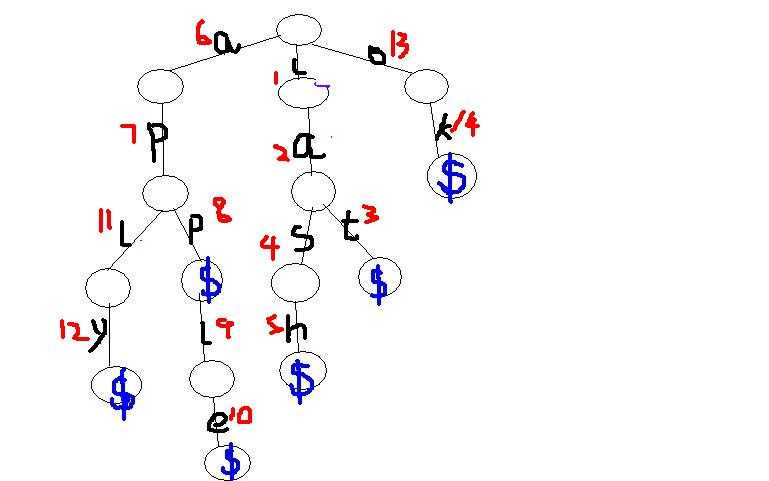
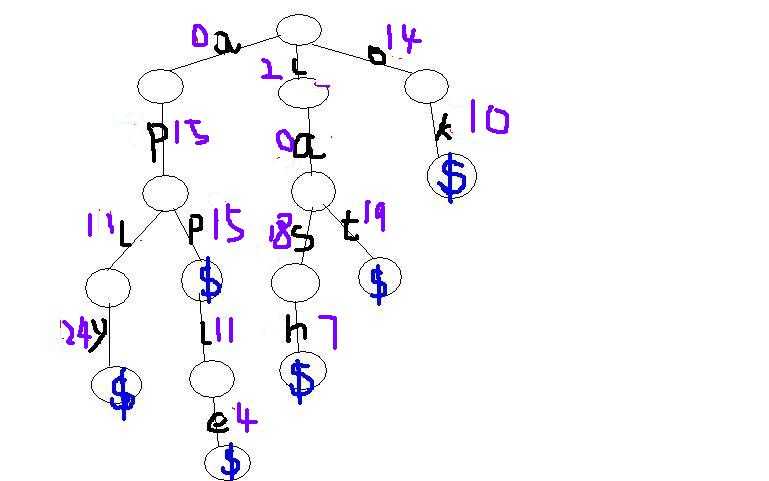
插入代码如下:
inline void insert() { int len=strlen(s); int root=0; for(int i=0;i<len;i++){ int id=s[i]-‘a‘; if(!t[root][id]) t[root][id]=++tot; root=t[root][id]; } }
2,查找search
查找一个单词也很容易,从根节点开始,如果有相同前缀就继续向下遍历,知道完整地查找完整个单词或者发现单词不存在这棵树上为止
代码:
inline void search() { int len=strlen(s); int root=0,k=0; while(1){ int id=s[k]-‘a‘; if(!t[root][id]) break; root=t[root][id]; k++; if(k==len)break; } if(k==len)printf("YES\n"); else printf("NO\n"); }
当然这两种也只是最基本的操作,至于其他操作我这里就不多讲了(懒癌晚期),网上大佬们的博客里都讲的很清楚了,这里再放一个模板题的代码:

//It is made by HolseLee on 6th Feb 2018 //Codevs P4189 #include<cstdio> #include<cstring> #include<cstdlib> #include<cmath> #include<iostream> #include<algorithm> #include<queue> using namespace std; int n,m,tot; char s[11]; int t[2000020][26]; inline void insert() { int len=strlen(s); int root=0; for(int i=0;i<len;i++){ int id=s[i]-‘a‘; if(!t[root][id]) t[root][id]=++tot; root=t[root][id]; } } inline void check() { int len=strlen(s); int root=0,k=0; while(1){ int id=s[k]-‘a‘; if(!t[root][id]) break; root=t[root][id]; k++; if(k==len)break; } if(k==len)printf("YES\n"); else printf("NO\n"); } void ready() { scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%s",s); insert();} } void work() { scanf("%d",&m); for(int i=1;i<=m;i++){ scanf("%s",s); check();} } int main() { ready(); work(); return 0; }

