Description
菩萨为行,福慧双修,智人得果,不忘其本。
——唐朠立《大慈恩寺三藏法师传》
有才而知进退,福慧双修,这才难得。
——乌雅氏
如何福慧双修?被太后教导的甄嬛徘徊在御花园当中。突然,她发现御花园中的花朵全都是红色和蓝色的。她冥冥之中得到了响应:这就是指导她如何福慧双修的! 现在御花园可以看作是有N块区域,M条小路,两块区域之间可通过小路连接起来。现在甄嬛站在1号区域,而她需要在御花园中绕一绕,且至少经过1个非1号区 域的区域。但是恰好1号区域离碎玉轩最近,因此她最后还是要回到1号区域。由于太后教导她要福慧双修,因此,甄嬛不能走过任何一条她曾经走过的路。但是, 御花园中来往的奴才们太多了,而且奴才们前行的方向也不一样,因此甄嬛在走某条小路的时候,方向不同所花的时间不一定一样。天色快暗了,甄嬛需要尽快知道 至少需要花多少时间才能学会如何福慧双修。如果甄嬛无法达到目的,输出“-1”。
Input
第一行仅2个正整数n,m,意义如题。
接下来m行每行4个正整数s,t,v,w,其中s,t为小路所连接的两个区域的编号,v为甄嬛从s到t所需的时间,w为甄嬛从t到s所需的时间。数据保证无重边。
Output
仅一行,为甄嬛回到1号区域所需的最短时间,若方案不存在,则输出-1
Sample Input
1 2 2 3
2 3 1 4
3 1 5 2
Sample Output
HINT
[样例解释]
对于第一个数据:路径为1->2->3->1,所需时间为8,而1->3->2->1所花时间为9。因此答案为8.
[数据范围与约定]
对于40%的数据:n<=1,000; m<=5,000
对于100%的数据:1<=n<=40,000; 1<=m<=100,000; 1<=v,w<=1,000
题目大意
给定一个有向图,对于连接同两个点的边算作同一条,问不经过重复边的最小正权环。保证没有重边(这个是指有向的),没有自环。
这道题经典就在于需要利用许多隐藏的性质。
如果想要暴力,那么建图多半会这么建:
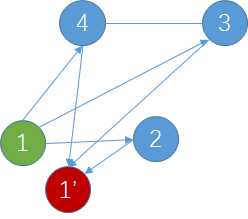
(ps:突然发现用ppt来画图特别赞)
比如显而易见的第一条性质
性质1 从1号点开始spfa,回到点1’,发生重复走的边一定是直接与1相连的边
因为在中途一条边走两次,等于你回到原地,那么肯定不优,所以spfa不会这么干。
于是就得到了一个优美的暴力做法,枚举1刚走出的那条边是哪条,然后删掉它的"反向边",然后最短路跑回来。于是菊花图横空出世,这个暴力做法完美TLE。
刚刚干掉了不合法的方案,现在来思考一下如何干掉不优的方案。
考虑最优的方案一定具有的性质。
-
如果最优的方案是直接跑最短路到达一个直接和1相连的点,但不是刚走出去的点。将它回到1的最后一条边记为$e_{1}$
性质2 没有更优的路径通过$e_{1}$作为最后一条边。
考虑用反证法,假设存在,那么它和最短路的性质矛盾。所以不存在。
-
考虑用$p_{i}$表示从1号点出发,到达点$i$的最短路径上的第二个点(刚离开1到达的点)。约定$p_{1} = -1$。
性质3 最优的路径除了上面那种情况,路径上仅存在1对直接相邻的点对$(u, v)$,且$u \neq 1, v \neq 1$,满足$p_{u} \neq p_{v}$
假如存在不为1对。如果存在0对,那么就是上面那种情况。如果存在2对及其以上,比如下面这样
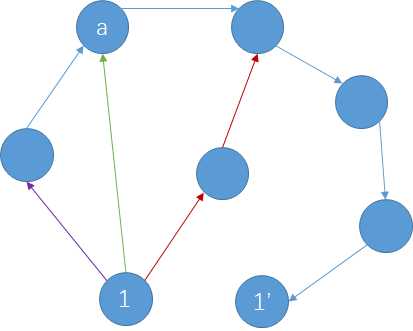
图中染有紫色、绿色和红色的边表示到某些点最短路径。那么显然走$1\rightarrow a\rightarrow 1‘$会比之前的方案更优。可以一直像这么做,直到满足条件为止。
既然性质3这么优美,那么考虑如何好好利用它。
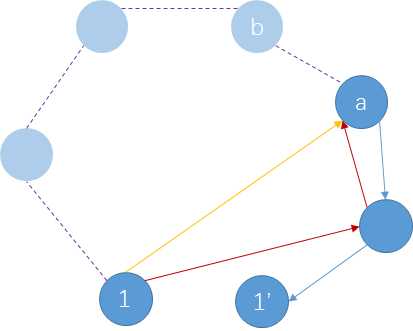
考虑边$(b, a, w)$的时候(满足$p_{a} \neq p_{b},a \neq 1, b\neq 1$),就在新图中中建一条边$(1, a, f_{b} + w)$(其中$f_{b}$表示原图中1到b的最短路长度)。
如果边$(b, a, w)$,满足$p_{a} = p_{b},a \neq 1, b\neq 1$,那么就保留这么一条边。
考虑边$(1, v, w)$,如果满足$p_{v} = v$,那么就不管它。这样可以使得新图中的合法路径满足性质3。
然后再考虑如何好好利用性质2和性质1。
对于边$(u, 1, w)$,如果满足$p_{u}\neq u$,那么直接在新图中加边$(1, 1‘, f_{u} + w)$
对于边$(u, 1, w)$,如果满足$p_{u} = u$,那么在新图中加边$(u, 1‘, w)$。
还剩一种情况
对于边$(1, v, w)$,满足$p_{v} \neq v$如何处理。上面似乎没有和它有关的性质。
这个保不保留你随意,我试了试,保不保留都AC了。
原题的答案就是在新图中1到1’的最短路。
最优性比较显然,相信还有疑问,就是不会会出现走重复的边的情况。
根据性质1,我们只需要考虑是否存在一种情况满足$1\rightarrow u\rightarrow 1‘$的情况。
对于点$u$如果$p_{u} = u$,那么新图中的$u$只会和$1‘$连边,否则只有边连向$u$或者没有有关$u$和1的连边。所以不存在这种情况。
最后%%% ZJC一发,这人太强了。。一年前做这道题,我只会dfs,他想出了正解。
Code
1 /** 2 * bzoj 3 * Problem#4398 4 * Accepted 5 * Time: 416ms 6 * Memory: 6620k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 typedef class Edge { 13 public: 14 int end; 15 int next; 16 int w; 17 18 Edge(int end = 0, int next = 0, int w = 0):end(end), next(next), w(w) { } 19 }Edge; 20 21 typedef class MapManager { 22 public: 23 int ce; 24 int *h; 25 Edge* es; 26 27 MapManager() { } 28 MapManager(int n, int m):ce(0) { 29 h = new int[(n + 1)]; 30 es = new Edge[(m + 5)]; 31 memset(h, 0, sizeof(int) * (n + 1)); 32 } 33 34 void addEdge(int u, int v, int w) { 35 es[++ce] = Edge(v, h[u], w); 36 h[u] = ce; 37 } 38 39 Edge& operator [] (int pos) { 40 return es[pos]; 41 } 42 }MapManager; 43 44 int n, m; 45 MapManager g; 46 MapManager ng; 47 int* f; 48 int* ps; 49 boolean *vis; 50 51 inline void init() { 52 scanf("%d%d", &n, &m); 53 f = new int[(n + 2)]; 54 vis = new boolean[(n + 2)]; 55 g = MapManager(n, m << 1); 56 ng = MapManager(n + 1, m << 1); 57 ps = new int[(n + 1)]; 58 for (int i = 1, u, v, x, y; i <= m; i++) { 59 scanf("%d%d%d%d", &u, &v, &x, &y); 60 g.addEdge(u, v, x); 61 g.addEdge(v, u, y); 62 } 63 } 64 65 inline void spfa(MapManager& g, int s, boolean record) { 66 queue<int> que; 67 memset(f, 0x3f, sizeof(int) * (n + 2)); 68 memset(vis, false, sizeof(boolean) * (n + 2)); 69 que.push(s); 70 f[s] = 0, ps[s] = s; 71 while (!que.empty()) { 72 int e = que.front(); 73 que.pop(); 74 vis[e] = false; 75 for (int i = g.h[e]; i; i = g[i].next) { 76 int eu = g[i].end, w = g[i].w; 77 if (f[e] + w < f[eu]) { 78 if (record) 79 ps[eu] = (e == 1) ? (eu) : (ps[e]); 80 f[eu] = f[e] + w; 81 if (!vis[eu]) { 82 vis[eu] = true; 83 que.push(eu); 84 } 85 } 86 } 87 } 88 } 89 90 inline void rebuild() { 91 spfa(g, 1, true); 92 for (int i = g.h[1]; i; i = g[i].next) { 93 int e = g[i].end; 94 if (ps[e] != e) 95 ng.addEdge(1, e, g[i].w); 96 } 97 for (int i = 2; i <= n; i++) { 98 for (int j = g.h[i]; j; j = g[j].next) { 99 int e = g[j].end; 100 if (e == 1) { 101 if (ps[i] == i) 102 ng.addEdge(i, n + 1, g[j].w); 103 else 104 ng.addEdge(1, n + 1, f[i] + g[j].w); 105 } else { 106 if (ps[i] == ps[e]) 107 ng.addEdge(i, e, g[j].w); 108 else 109 ng.addEdge(1, e, f[i] + g[j].w); 110 } 111 } 112 } 113 } 114 115 inline void solve() { 116 spfa(ng, 1, false); 117 printf("%d\n", f[n + 1]); 118 } 119 120 int main() { 121 init(); 122 rebuild(); 123 solve(); 124 return 0; 125 }
