洛谷P1003 铺地毯

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 n 张地毯，编号从 1 到n 。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入输出格式

输入格式：

输入文件名为carpet.in 。

输入共n+2 行。

第一行，一个整数n ，表示总共有 n 张地毯。

接下来的n 行中，第 i+1 行表示编号i 的地毯的信息，包含四个正整数 a ，b ，g ，k ，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标（a ，b ）以及地毯在x轴和y 轴方向的长度。

第n+2 行包含两个正整数 x 和y，表示所求的地面的点的坐标（x ，y）。

输出格式：

输出文件名为carpet.out 。

输出共1 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出-1 。

输入输出样例

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

3

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

-1

说明

【样例解释1】

如下图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，覆盖点（2,2）的最上面一张地毯是 3 号地毯。

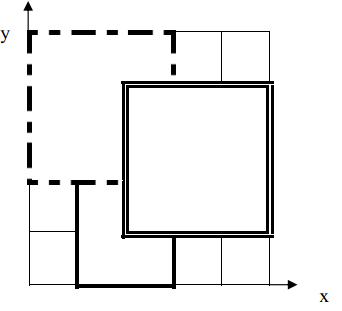
【数据范围】

对于30% 的数据，有 n ≤2 ；

对于50% 的数据，0 ≤a, b, g, k≤100；

对于100%的数据，有 0 ≤n ≤10,000 ，0≤a, b, g, k ≤100,000。

noip2011提高组day1第1题

分析

最近在刷洛谷的试炼场的普及组，关于这题，第一印象就是用数组去模拟，但是数据是不允许的。我们要有逆向的思维，虽然数据是正着输入的，但是我们可以反过来做的。如果有多个询问是否还能用这个方法去做呢？如果还是按照这种方法去做的话，应该能承受10000次的询问，应该算是最好的算法了吧，但不排除有其他的算法，但鄙人才学疏浅一时想不出来其他更高级(装X)的算法，就暂且放放。这道题会不会有变形，或者简化版本比如说一维的铺地毯，那样会不会方法给更多，就能拓展到二维了。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int n,a[N],b[N],c[N],d[N],x,y;
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
        scanf("%d%d%d%d",&a[i],&b[i],&c[i],&d[i]);
    scanf("%d%d",&x,&y);
    for(int i=n;i>=1;--i)
        if(a[i]<=x&&b[i]<=y&&a[i]+c[i]>=x&&b[i]+d[i]>=y){    
            printf("%d\n",i); return 0;
        }
    printf("-1\n");
    return 0;
}