现在真是一碰电脑就很颓废啊...
于是早晨把电脑锁上然后在旁边啃了一节课多的算导, 把FFT的基本原理整明白了..
但是我并不觉得自己能讲明白...
Fast Fourier Transformation, 快速傅里叶变换, 是DFT(Discrete Fourier Transform, 离散傅里叶变换)的快速实现版本.
据说在信号处理领域广泛的应用, 而且在OI中也有广泛的应用(比如SDOI2017 R2至少考了两道), 所以有必要学习一波..
划重点: 其实学习FFT最好的教材是《算法导论》, 里面讲的很是清楚, 建议大家用心把FFT这一章节通读一遍, 我这种zz也就看了大约一节课的时间就看完了w
在信号处理领域的应用我也不会也讲不了, 所以我们就说说求多项式乘法吧..
首先是多项式的定义: (我们不生产定义, 我们只是算导的搬运工)
\[
A(x)=\sum_{j=1}^{n-1}a_jx^j
\]
为什么循环变量不用\(i\)呢, 是因为要用到复数(后面会提到哒~
然后还有一些概念比如
- 系数: 每个\(a_i\). 所有系数属于域F, 典型的情形是复数集合C
- 次数: 最高次的非零系数为\(a_k\), 则次数为\(k\).
- 次数界: 任何一个严格大于多项式次数的整数. 因此, 对于次数界为\(n\)的多项式, 次数的取值范围是\(\{x\in N|0\leq x\leq n-1\}\)
然后是多项式的表达方式. 多项式的表达方式有两种: 系数表达和点值表达.
这个不难理解, 根据上面的定义, 一个次数界为\(n\)的多项式可以用一个由系数组成的向量\(a=(a_0,a_1,...a_{n-1})\)来唯一确定, 这个就是这个多项式的系数表达.
而点值表达则是说, 对于\(A(x)=\sum_{j=1}^{n-1}a_jx^j\)这个式子, 我们可以用一个至少包含\(n\)个不同的点的集合来唯一确定. 这个点集就是多项式的点值表达, 当然, 点值表达不是唯一的.
举个栗子: 有一个多项式\(A(x)=x^3+2x^2+4\), 它的系数表达可以是\(a=(1,2,0,4)\), 而点值表达则可以是\(\{(-1,4),(0,4),(1,6),(2,16)\}\).
然后我们就可以定义运算:
- 多项式的加法
对于系数表达来说, 大家已经非常熟悉了, 就是合并同类项嘛, 没什么好说的, 时间复杂度\(O(n)\)
对于点值表达来说, 我们可以选取\(x\)相同的\(n\)个点, 然后把\(y\)相加就行了, 时间复杂度也是\(O(n)\) - 多项式的乘法
对于系数表达来说, 是大家熟悉的形式, 就是一个多项式的每一项分别与另一个多项式的每一项相乘, 然后再合并同类项, 那么时间复杂度就是\(O(n^2)\)的.
对于点值表达来说, 我们依然选\(x\)相同的\(n\)个点, 然后把\(y\)相乘就行了, 时间复杂度依然是\(O(n)\)
不过有一点要注意, 就是\(C(x)\)的次数界不再是\(n\), 而是\(2n\)(因为次数界\(2n-1\)的多项式我们同样可以说次数界是\(2n\), 所以为了方便我们就说\(2n\)了),
所以我们要对点值进行扩展, 选取\(2n\)个点逐个相乘, 不过并不影响复杂度.
所以说在点值表达的情况下我们可以\(O(n)\)计算多项式的乘法, 但系数表达则不行. 那我们能不能让系数表达的多项式乘法快一点呢?
我们可以试图在比较好的复杂度下把系数表达转化为点值表达, 然后乘完再转化会系数表达..
(P.S. 我们管系数表达转化为点值表达的操作叫求值, 求值的逆操作叫插值.)
然后我们省略关于求值和插值的一吨证明过程(因为看的云里雾里
不过我们可以知道, 如果只是看心情取\(n\)个点代入计算点值的话, 求值的时间复杂度就是\(O(n^2)\);
而采用拉格朗日插值法, 就可以用\(O(n^2)\)的时间复杂度来进行插值.
但这显然不是我们想要的复杂度.
这时候就需要FFT了, 通过精心的挑选求值点, 我们可以巧妙地将两种表达间的转化的复杂度降为\(O(nlogn)\).
那我们就可以通过系数->点值->系数的方式, 用\(O(nlogn)\)的复杂度完成系数表达下的多项式乘法.
那要怎么选点呢? 我们选取的是单位复数根.
蛤? 这是个什么玩意? (点上面的链接去baidu看一下咯~
\(n\)次单位复数根就是满足\(\omega^n=1\)的复数\(\omega\). 因为\(n\)次方程有\(n\)个复根, 所以\(n\)次单位复数根有\(n\)个.
这\(n\)个根分别是\(e^{2\pi ik/n} (k=0,1,2,...,n-1)\). 为了解释这玩意, 我们利用复数的质数形式的定义
\[
e^{iu}=\cos(u)+i\sin(u)
\]
然后这几个根是均匀的分布在以复平面的原点为圆心的单位半径的圆周上的.
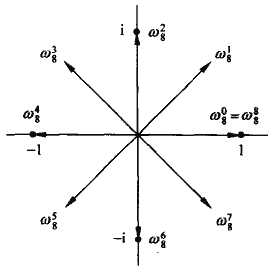
其中\(\omega_n=e^{2\pi i/n}\)称为主\(n\)次单位根, 所有其他\(n\)次单位复根都是它的幂次.
然后就是一堆引理... 只是贴一下(要不是有用贴都不想贴), 证明见算导P532
消去引理: 对于任何整数\(n\geq0,k\geq0\), 以及\(d>0\), \(\omega_{dn}^{dk}=\omega_n^k\)
推论: 对于任意偶数\(n>0\), 有\(\omega_n^{n/2}=w_2=-1\).
折半引理: 如果\(n>0\)为偶数, 那么\(n\)个\(n\)次单位复根的平方的几何就是\(n/2\)个\(n/2\)次单位复数根的集合.
求和引理: 对于任意整数\(n\geq 1\)和不能被\(n\)整除的非负整数\(k\), 有
\[ \sum_{j=0}^{n-1}(\omega_n^k)^j=0 \]
回到我们的多项式乘法问题, 我们希望计算次数界为\(n\)的多项式 (这里的\(n\)已经是原数据规模中\(n'\)的两倍了)
\[
A(x)=\sum_{j=0}^{n-1}a_jx^j
\]
在\(n\)次单位复根处的取值, 而此时我们有一个系数向量\(a=(a_0,a_1,...a_{n-1})\), 我们令
\[
y_k=A(\omega_n^k)=\sum_{j=0}^{n-1}a_j{\omega_n^k}^j
\]
我们就可以获得一个点值向量\(y=(y_0,y_1,...,y_{n-1})\)., 我们称\(y\)为\(a\)的离散傅里叶变换(传说中的DFT) , 也可以记为\(y=DFT_n(a)\).
好的现在重头戏登场, 我们来讲一下FFT.
首先显然直接计算DFT的复杂度是\(O(n^2)\), 那怎么优化呢? 这就要用到了我们非常常见的一种思想: 分治!
我们第一步做一个合理(?)的假设, \(n\)是2的整数次幂. 那如果不是呢? 有别的(更好(nan)的)方法, 但是我们不用.
我们就强行扩充成2的整数次幂...(好像zkw线段树也是这么干的..) 如果原问题的数据规模是513, 我们也要扩充成1024, 然后再翻个倍变成2048.. (好像有点浪费?)
然后FFT利用了分治的策略, 将奇数项和偶数项分别提出来.
\[
A(x)=(a_0+a_2x^2+a_4x^4+...+a_{n-2}^x{n-2})+(a_1x+a_3x^3+a_5x^5+...+a_{n-1}x^{n-1})
\]
然后我们把两个括号分别搞成两个式子, 从后面的括号里提一个\(x\), 然后换元, 用\(x\)来表示\(x^2\), 能得到
\[
A^{[0]}(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{n/2-1}\A^{[1]}(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{n/2-1}\A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)
\]
这样我们就把问题转化为了求次数界为\(n/2\)的多项式\(A^{[0]},A^{[1]}\)在点\((\omega_n^0)^2,(\omega_n^1)^2,...,(\omega_n^{n-1})^2\)处的取值.
而根据折半引理, 这\(n\)个取值是由\(n/2\)个值每个值出现两次构成的, 问题规模就从\(n\)变成了\(n/2\), 所以我们继续递归分治下去就可以求出来了.
时间复杂度\(T(n)=2T(n/2)+O(n)=>O(nlogn)\).
根据上面的思路我们就可以写出伪代码.. (决定向zky神犇一样用python的高亮...
# 伪代码哟~
FFT(a,n): # 求一个n维向量a的DFT
if(n==1):
return a # 递归终止的条件
wn=e^(2*pi*i/n)=cos(2*pi/n)+sin(2*pi/n)*i # 定义枚举(旋转)的方向, 这个是逆时针旋转的(编号递增)
a0=[a_0,a_2,...,a_n-2]
a1=[a_1,a_3,...,a_n-1] # 按照奇偶分成两半
y0=FFT(a0,n/2)
y1=FFT(a1,n/2) # 递归处理
for k in range(0,n/2): # 合并操作
y[k]=y0[k]+w*y1[k]
y[k+n/2]=y0[k]-w*y1[k] # 折半引理
w=w*wn #下一个单位复根
return y差不多就是这样, 如果上面基本理解的话这里应该就没啥太大问题了.. 看不懂的话算导P534有将近一页的对伪代码的补充说明...
然后我们已经能求值了, 现在来考虑插值.
哎呀证明什么的又要用到矩阵 啊看不懂.... 知道能证明就行了...
我们可以欣赏编写算导的人一步一步推导出逆DFT(又称IDFT) \(DFT_n^{-1}(y)\):
\[
a_j=\frac1n\sum_{k=0}^{n-1}y_k{\omega_n^{-k}}^j
\]
然后我们跟之前求DFT要求的
\[
y_k=A(\omega_n^k)=\sum_{j=0}^{n-1}a_j{\omega_n^k}^j
\]
比较一下, 可以得出, 我们只需要把\(a,y\)互换, 用\(\omega_n^{-1}\)替换\(\omega_n\), 最后将计算结果都除以\(n\)就行了.
这样我们就可以很轻松地写(chao)出伪代码: (顺便完成了练习30.2-4
IFFT(a,n): # 求一个n维向量a的DFT
if(n==1):
return a # 递归终止的条件
wn=e^(2*pi*i/n)=cos(2*pi/n)-sin(2*pi/n)*i # 顺时针
y0=[y_0,y_2,...,y_n-2]
y1=[y_1,y_3,...,y_n-1]
a0=FFT(y0,n/2)
a1=FFT(y1,n/2)
for k in range(0,n/2): # 合并操作
a[k]=a0[k]+w*a1[k]
a[k+n/2]=a0[k]-w*a1[k] # 折半引理
w=w*wn #下一个单位复根
return a这样我们也完成了\(O(nlogn)\)的IDFT. 我们已经可以\(O(nlogn)\)解决FFT问题了.
我们研究一个算法肯定是要尽可能的快, 所以我们考虑能不能优化一下算法的常数.
首先我们看到循环里面有两个\(\omega_n^k*y_k^{[1]}\), 我们可以采用一个局部变量\(t\)来存一下, 把循环搞成这样:
for k in range(0,n/2):
t=w*y1[k]
y[k]=y0[k]+t
y[k+n/2]=y0[k]-t
w=w*wn这个操作有个很好听的名字, 叫"蝴蝶操作".
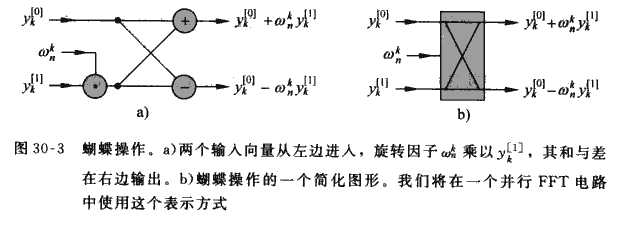
好像什么对称的东西都能想到蝴蝶?? (脊髓灰质瑟瑟发抖) 果然是贫穷限制了我的想象力吧~
然后我们就可以化一下递归树, 来找一下规律. 我们发现这棵树是长这样的:
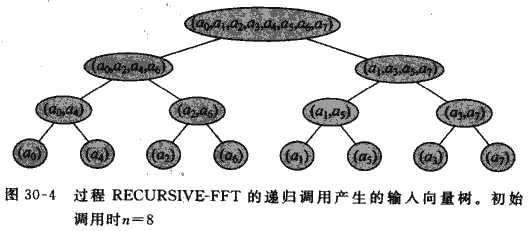
这样我们发现其实调用的时候并非是自顶向下, 而是自底向上, 所以我们可以试着把递归改成迭代.
我们看一下最底层有什么规律. 我们把这些数的下标化成二进制:
000 100 010 110 001 101 011 111
那这不就是0~7分别的二进制倒过来嘛...
我们可以非常容易地处理出这个数组. 算导上甚至认为特别简单都没有给代码...
我们用C++写起来大约可以这样(各种奇怪的位运算):
void rev(cp *ar){
memset(vis,0,sizeof(vis));
for(ri i=1;i<n-1;++i){
int x=i,y=0;
if(vis[x]) continue;
for(ri j=1;j<n;j<<=1)
y=(y<<1)|(x&1),x>>=1;
vis[i]=vis[y]=1; swap(ar[i],ar[y]);
}
}然后我们就可以把代码改成:
for s in range(1,(logn)+1):
for k in range(0,n-1,2**s):
combine... # 这一行太长了 想看的去算导翻吧, 反正写这一句也没啥用那么我们把这一行拆开是得到下面的伪代码:
FFT2(a,n):
REVERSE(a) # 数组归位
for s in range(1,(logn)+1): # 枚举层数
m=2**s #处理的长度
wm=cos(2*pi/m)+i*sin(2*pi/m) #在这一层的单位根的旋转单位
for i in range(0,m/2): #上面的k
t=w*a[k+j+m/2]
u=a[k+j] #防止被覆盖 多申请一个变量
a[k+j]=u+t
a[k+j+m/2]=u-t
w=w*wm
return a这样我们就成功把递归改成了迭代, 节约了常数..
复杂度是没有改变的, 证明见算导P538中间.
这样我们就讲完了..
有一道练习题, 高精度乘法
首先朴素的高精度乘法是\(O(n^2)\)的, 好像\(n\leq6*10^4\)压位可过...
不过我们还是来练习一下FFT..
我们可以把一个大整数视为一个
\[
\sum_{j=0}^{n-1}a_j10^j
\]
的一个多项式, 我们用FFT求出乘积的多项式的各个系数, 然后依次处理一下进位, 去掉前导0就可以咯~
C++实现代码:
#include <cmath>
#include <cstdio>
#include <vector>
#include <cstring>
#define ri register int
using namespace std;
const int N=150000;
const double pi=acos(-1);
const double eps=1e-9;
struct cp{
double r,i;
cp(double R=0,double I=0):r(R),i(I){}
}; //手写复数(据说用STL的complex会T?)
cp a[N],b[N];bool vis[N];int n=1;
cp operator+(const cp& a,const cp& b){return cp(a.r+b.r,a.i+b.i);}
cp operator-(const cp& a,const cp& b){return cp(a.r-b.r,a.i-b.i);}
cp operator*(const cp& a,const cp& b){return cp(a.r*b.r-a.i*b.i,a.r*b.i+a.i*b.r);}
void rev(cp *ar){
memset(vis,0,sizeof(vis));
for(ri i=1;i<n-1;++i){
int x=i,y=0;
if(vis[x]) continue;
for(ri j=1;j<n;j<<=1)
y=(y<<1)|(x&1),x>>=1;
vis[i]=vis[y]=1; swap(ar[i],ar[y]);
}
}
void fft(cp *y,bool f){ rev(y);//f=true表示IDFT f=false表示DFT
for(ri m=2;m<=n;m<<=1){
cp wm(cos(2*pi/m),f?sin(2*pi/m):-sin(2*pi/m));
for(ri k=0;k<n;k+=m){
cp w(1,0);
for(ri j=0;j<m/2;++j){
cp t=w*y[k+j+m/2],u=y[k+j];
y[k+j]=u+t;
y[k+j+m/2]=u-t;
w=w*wm;
}
}
}
if(!f) for(int i=0;i<n;++i) y[i].r/=n;
}
char c1[N],c2[N];int c[N];
int main(){
int nn,l1,l2; scanf("%d",&nn);
for(n=1;n<nn;n<<=1); n<<=1;
scanf("%s%s",c1,c2);
l1=strlen(c1),l2=strlen(c2);
for(ri i=0;i<l1;++i)a[i]=cp(c1[l1-i-1]-48);fft(a,1); //DFT a
for(ri i=0;i<l2;++i)b[i]=cp(c2[l2-i-1]-48);fft(b,1); //DFT b
for(ri i=0;i<n;++i)a[i]=a[i]*b[i];fft(a,0); //IDFT a*b
for(ri i=0;i<n;++i)c[i]=a[i].r+0.5; //这个地方要四舍五入(精度感人)
for(ri i=0;i<n;++i)c[i+1]+=c[i]/10,c[i]%=10; //处理进位
while(!c[n]&&n>0) --n; //干掉前导0
for(ri i=n;i>=0;--i)putchar(c[i]+48);
}python实现代码:
n=int(input())
a=int(input())
b=int(input())
print(a*b)(废话, 这种题有python谁写FFT啊..)
py大法好!!
就这样吧~
