标签：ado   原因   ogr   http   col   基于   应该   oss   就是   

旗子用的是plane，不要用cube，这是基于顶点计算的，cube算来算去只有八个顶点，根本飘不起来
而且我们把plane绕x轴转90度把它立起来
所以它本身的坐标是：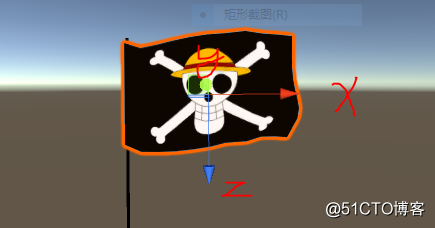

x轴水平向右，z轴垂直向下，y轴垂直向里
shader代码:

//1.
Shader "Custom/SKFlag" {
    Properties{
        _MainTex("Main",2D)=""{}
        _A("A",range(0.1,3))=1
        _F("F",range(0.1,2))=1
        _Edge("Edge",range(-10,10))=0
        _TimeScale("TimeScale",range(0,20))=2
    }
    SubShader {
        pass{
            cull off                         //2.
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            #include "unitycg.cginc"
            #include "lighting.cginc"
            sampler2D _MainTex;
            float4 _MainTex_ST;
            float _A;
            float _F;
            float _TimeScale;
            float _Edge;
            struct v2f{
                float4 pos:POSITION;
                float2 uv:TEXCOORD0;
            };
            v2f vert(appdata_base v)
            {
                v2f o;
                o.pos=v.vertex;
                if(o.pos.x>_Edge)             //3.
                {
                    o.pos.y+=_A*0.8*sin(_F*(o.pos.x+o.pos.z)+_Time.y*_TimeScale*0.6);     //4.
                    o.pos.z+=_A*0.3*sin(_F*(o.pos.x+o.pos.y)+_Time.y*_TimeScale*0.6);     //5.
                }
                if(o.pos.x>-1)
                {
                    o.pos.y+=_A*0.3*sin(_F*(o.pos.x+o.pos.z)+_Time.y*_TimeScale*0.8);

                }
                if(o.pos.x>1)
                {
                    o.pos.y+=_A*0.8*sin(_F*(o.pos.x+o.pos.z)+_Time.y*_TimeScale*0.8);
                    o.pos.x+=_A*0.2*sin(_F*(o.pos.z+o.pos.y)+_Time.y*_TimeScale*0.3);
                }
                if(o.pos.x>3)
                {
                    o.pos.y+=_A*0.8*sin(_F*(o.pos.x+o.pos.z)+_Time.y*_TimeScale*0.2);
                }

                o.pos=mul(UNITY_MATRIX_MVP,o.pos);
                o.uv=TRANSFORM_TEX(v.texcoord,_MainTex);
                return o;
            }
            fixed4 frag(v2f IN):COLOR
            {
                fixed4 col=tex2D(_MainTex,IN.uv);
                return col;
            }
            ENDCG
        }
    }
}

先看一个函数：f(x)=Asin(ωx+φ)
A：振幅,函数最大值为A,最小值为-A；ω：角频率 ；φ：初相,即x=0时的相位ωx+φ
再看我们的代码

1

定义的属性中有主材质，放海盗旗的图
_A：振幅
_F：角频率
_TimeScale：时间函数乘上的系数
_Edge：这个是x方向坐标的边界后面说明

2

cull off

默认是剔除背面

cull back

也就是plane只能看到一面，而看不到另一面的原因，改成cull off，不剔除背面，则两面都是旗子

3

这里是第一个判断处

if(o.pos.x>_Edge)             //3.

纵观整个代码，旗子在三个方向都会有波动，但是，如果旗子是插在旗杆上的话，那与旗杆的连接处是不应该有波动的
也就是图中旗子在x轴方向上的最左侧，即x值最小处
经过试验，这个值应该是 -5，所以我设置的_Edge为 -4.9，那么只有在x坐标大于这个值的部分，plane才会波动

4、5

这些，还有下面的那些就是让plane产生波动的计算了
_A是波动（飘扬）的最大幅度，_Time是时间向量，好像也是四维的，xyzw

_Time.y*_TimeScale

这个可以看作是波动的频率快慢吧
调整_TimeScale的值越大，波动的越快
而_F*（...）呢，我的理解是影响波长，_F越大，波长越小，同一时间旗子上的波峰波谷越多，反之越少
不知道理解的正不正确，反正出来的效果差不多是这样

ShaderLab学习小结（十七）草帽团的旗子

标签：ado   原因   ogr   http   col   基于   应该   oss   就是   

原文地址：http://blog.51cto.com/shuxiayeshou/2070276