Clustering

Unsupervised learning introduction

什么是非监督学习呢?

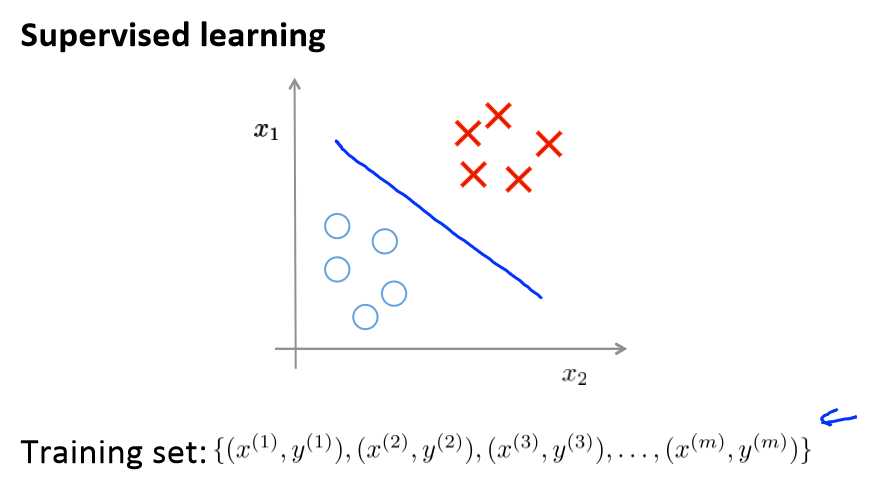
在一个典型的监督学习中，我们有一个有标签的训练集，我们的目标是找到能够区分正样本和负样本的决策边界，在这里的监督学习中，我们有一系列标签，我们需要据此拟合一
个假设函数。

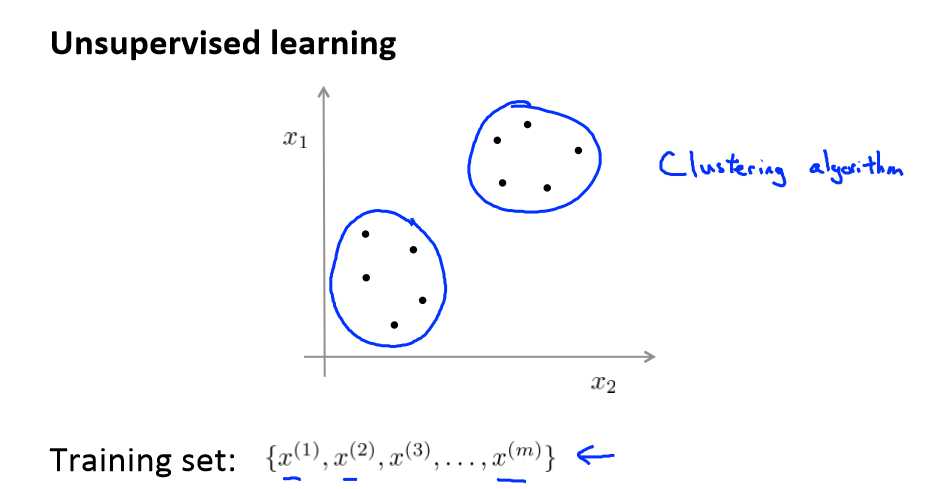
与此不同的是，在非监督学习中，我们的数据没有附带任何标签，我们拿到的数据就是这样的：

在这里我们有一系列点，却没有标签。因此，我们的训练集可以写成只有 x⁽¹⁾,x⁽²⁾…..一直到 x^(m)。我们没有任何标签 y。也就是说，在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，然后我们告诉这个算法，快去为我们找找这个数据的内在结构给定数据。我们可能需要某种算法帮助我们寻找一种结构。

想上图一样，根据相同的特点分成一类，上面分成两类。

还有类似的例子：

K-­means algorithm（K-均值算法）

假设有下面这些数据：

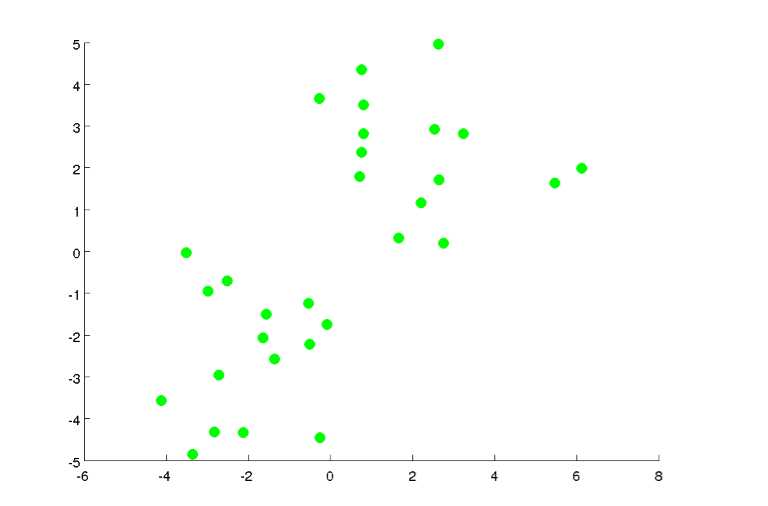
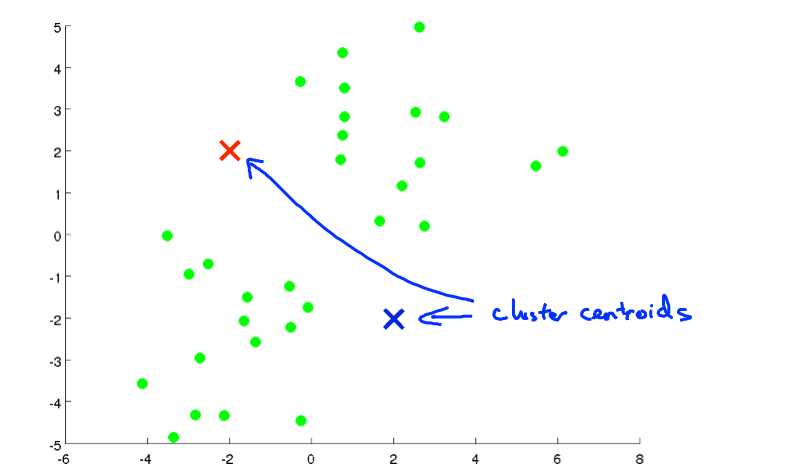
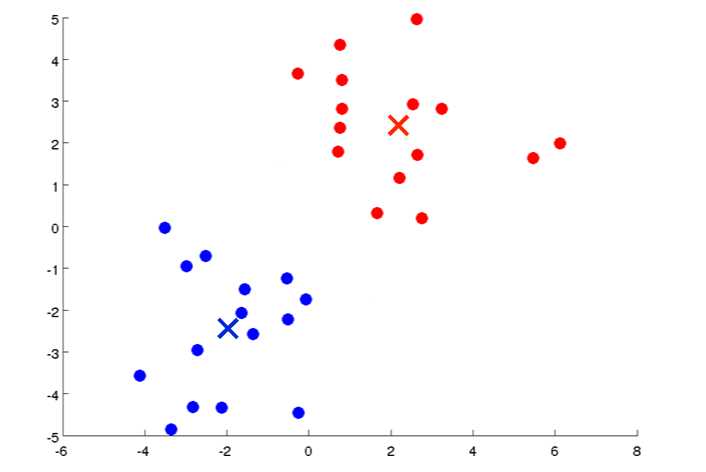
如果我们要分成两类，先随机选择两个点：

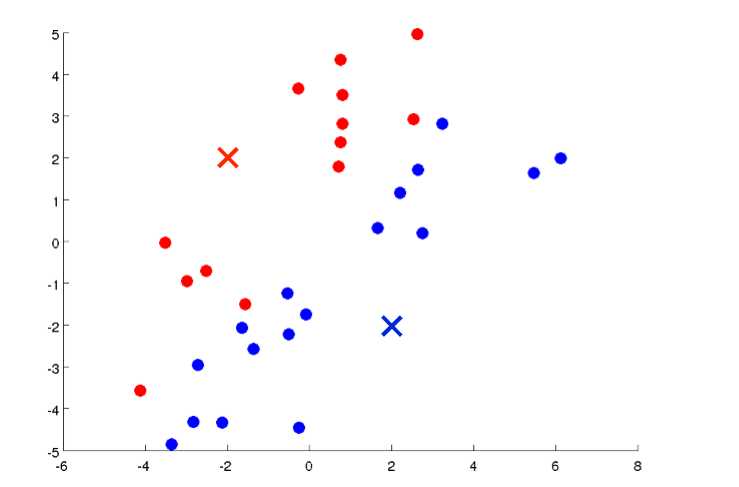
然后其它离红点近的归红色一类，离蓝点进的归蓝色一类：

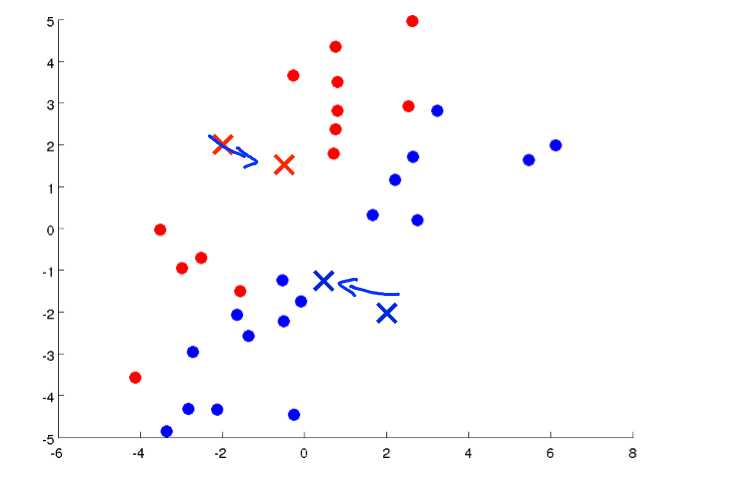
然后红色和蓝色这些点算出它们的中心点：

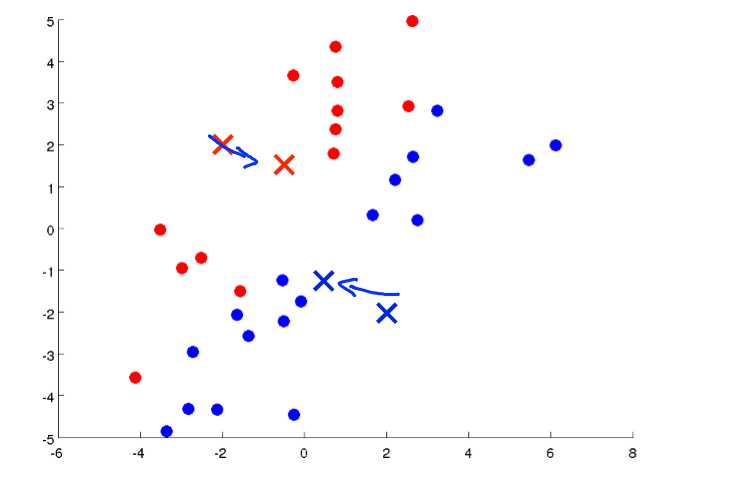
选择的中点后有重复以上步骤：

最终就会在两个点处不同，说明算完了，已经成功的分成了两类;

分成三类也类似：

Optimization objective（优化目标）

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此 K-均值的代价函数（又称畸变函数 Distortion function）为：

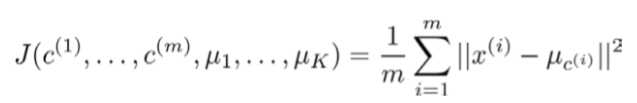
其中μ_c⁽ⁱ⁾代表与x⁽ⁱ⁾最近的聚类中心点。我们的的优化目标便是找出使得代价函数最小的 c⁽¹⁾,c⁽²⁾,...,c^(m)和 μ₁,μ₂,...,μ_k：

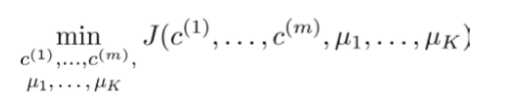
回顾刚才给出的 K-均值迭代算法，我们知道，第一个循环是用于减小 c⁽ⁱ⁾引起的代价，而第二个循环则是用于减小 μ_i 引起的代价。迭代的过程一定会是每一次迭代都在减小代价
函数，不然便是出现了错误。

Random initialization

在运行 K-均值算法的之前，我们首先要随机初始化所有的聚类中心点，下面介绍怎样做：
1、我们应该选择 K<m，即聚类中心点的个数要小于所有训练集实例的数量 

2、随机选择 K 个训练实例，然后令 K 个聚类中心分别与这 K 个训练实例相等 

K-均值的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。

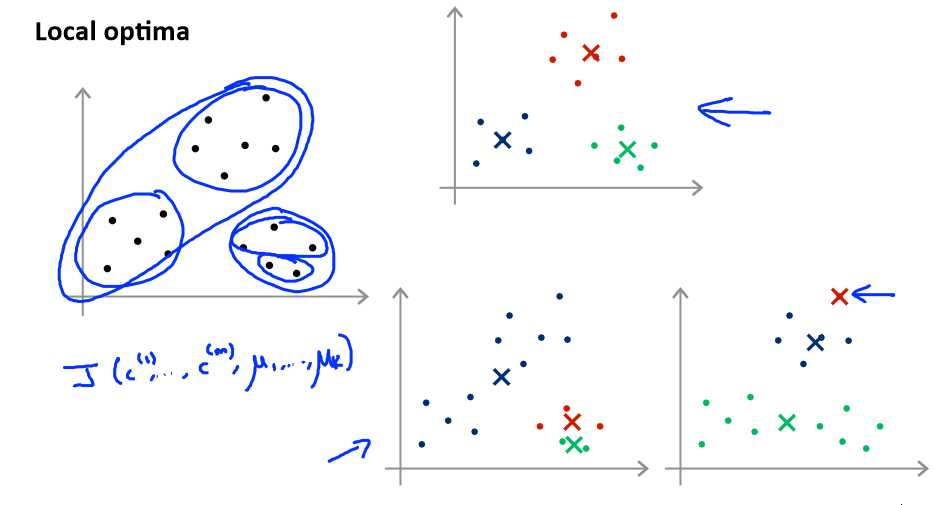
为了解决这个问题，我们通常需要多次运行 K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行 K-均值的结果，选择代价函数最小的结果。这种方法在 K 较小的时
候（2--10）还是可行的，但是如果 K 较大，这么做也可能不会有明显地改善。

Choosing the number of clusters

使用K-均值迭代算法关键是K选择多少。

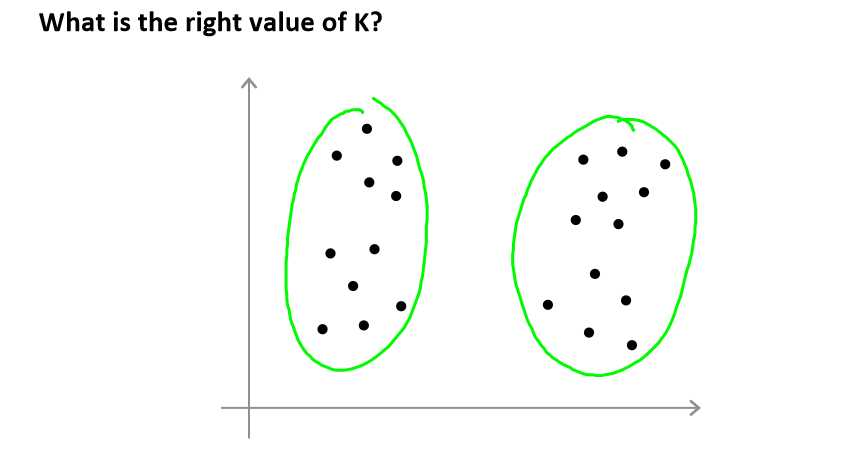
上图可以选择两个，但也可以选择4个，那么选择哪个是最好的呢？

这时我们用到的是“肘部法则”

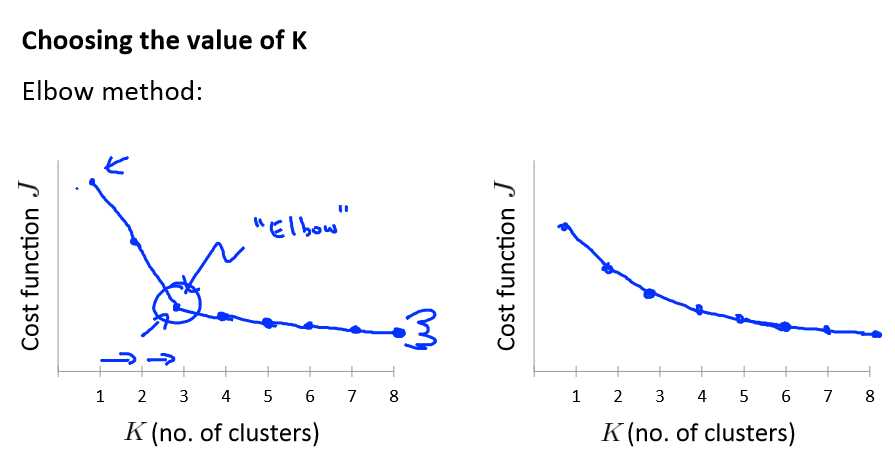
选择肘部位置所代表的K值是最好了。

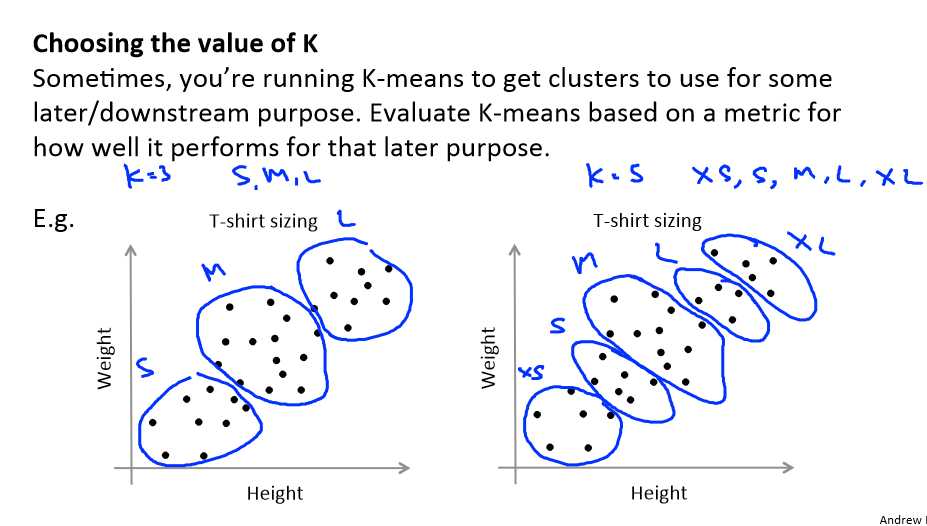
Dimensionality Reduction(降维)

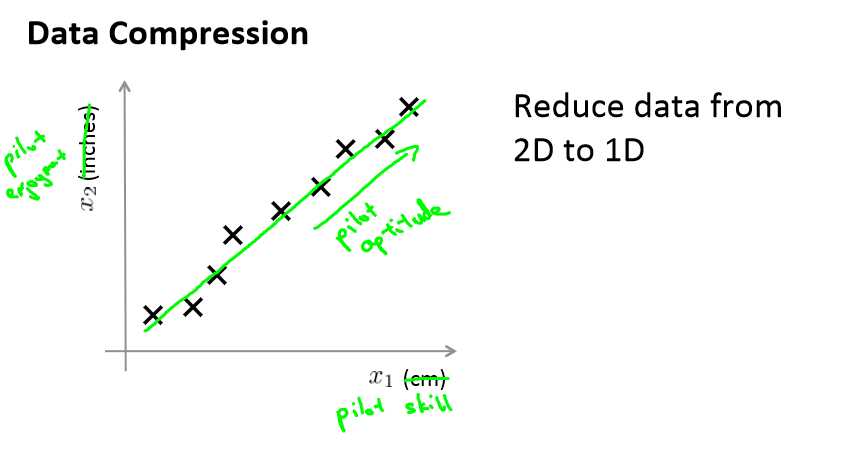
Motivation I: Data Compression（数据压缩）

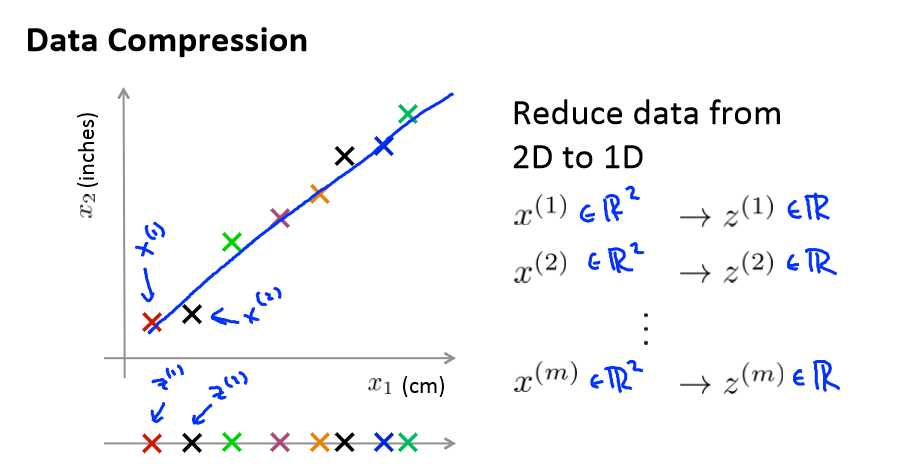
x₁表示厘米，x₂表示英寸，很明显，x₁和x₂可以用一个特征变量表示，就可以从二维降到一维了。

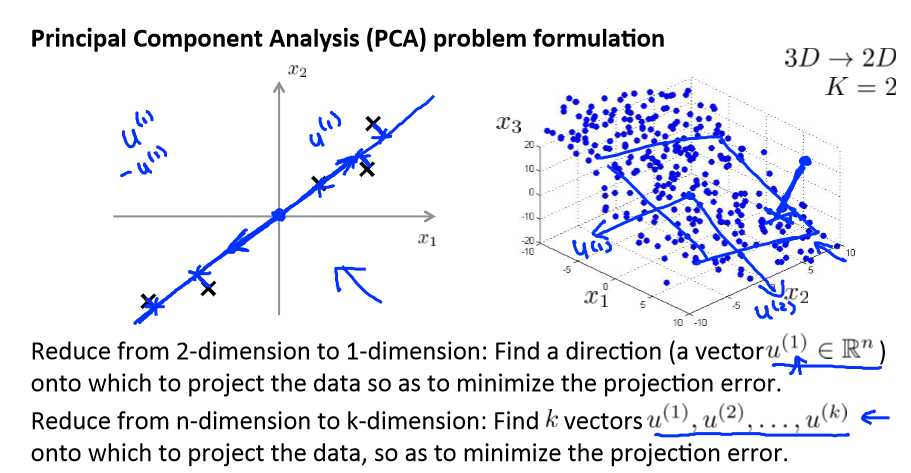
将数据从三维降至二维： 这个例子中我们要将一个三维的特征向量降至一个二维的特征向量。过程是与上面类似的，我们将三维向量投射到一个二维的平面上，强迫使得所有的
数据都在同一个平面上，降至二维的特征向量。

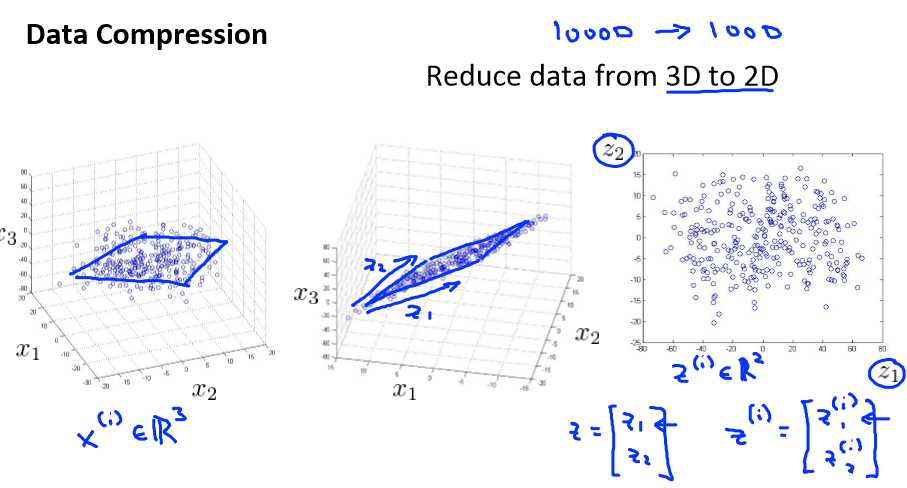
这样的处理过程可以被用于把任何维度的数据降到任何想要的维度，例如将 1000 维的特征降至 100 维。

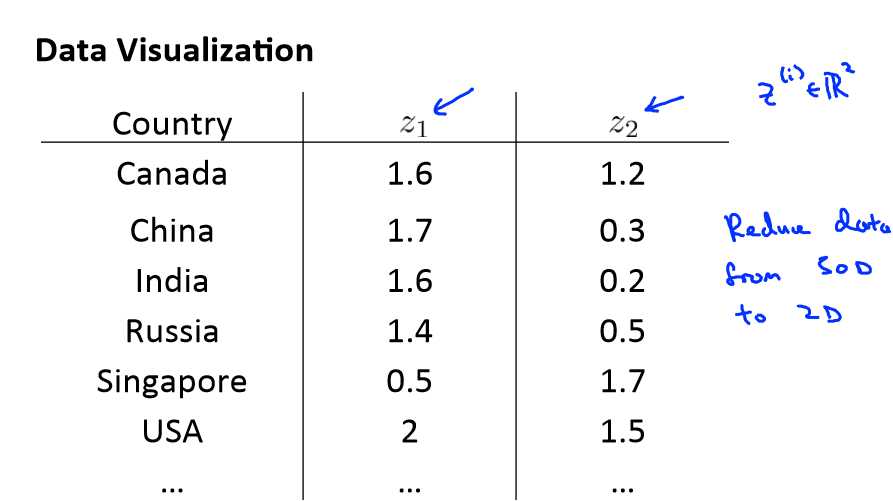
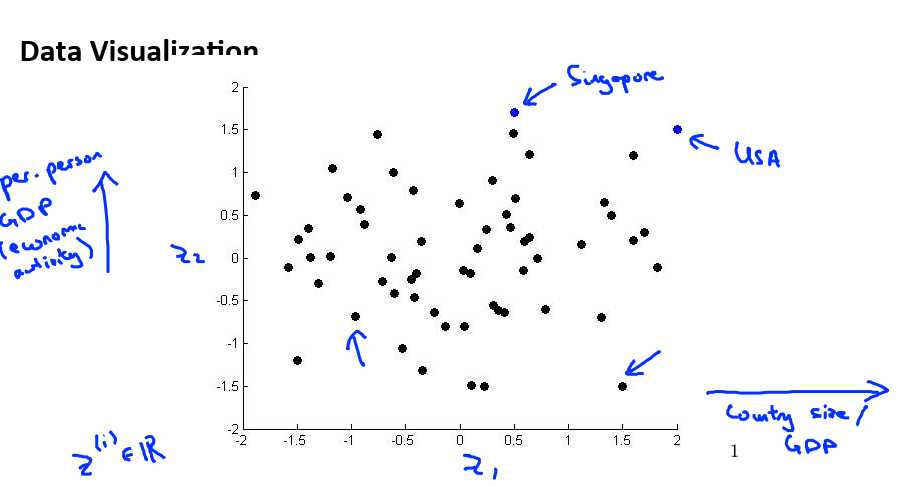
Motivation II: Data Visualization  （数据可视化）

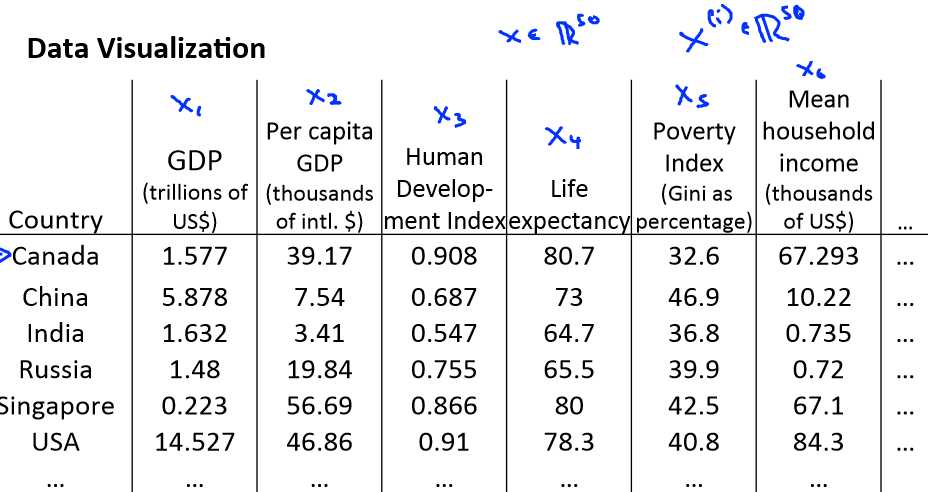
假使我们有有关于许多不同国家的数据，每一个特征向量都有 50 个特征（如，GDP，人均 GDP，平均寿命等）。如果要将这个 50 维的数据可视化是不可能的。使用降维的方法
将其降至 2 维，我们便可以将其可视化了。

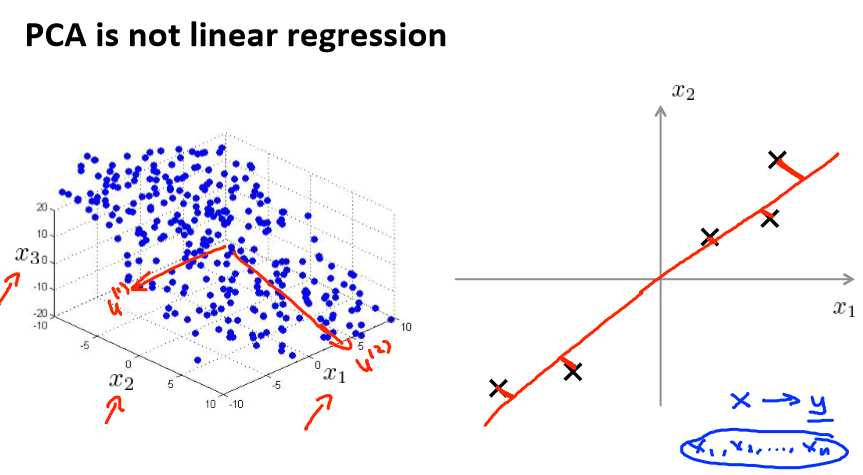
Principal Component Analysis problem formulation（PCA）

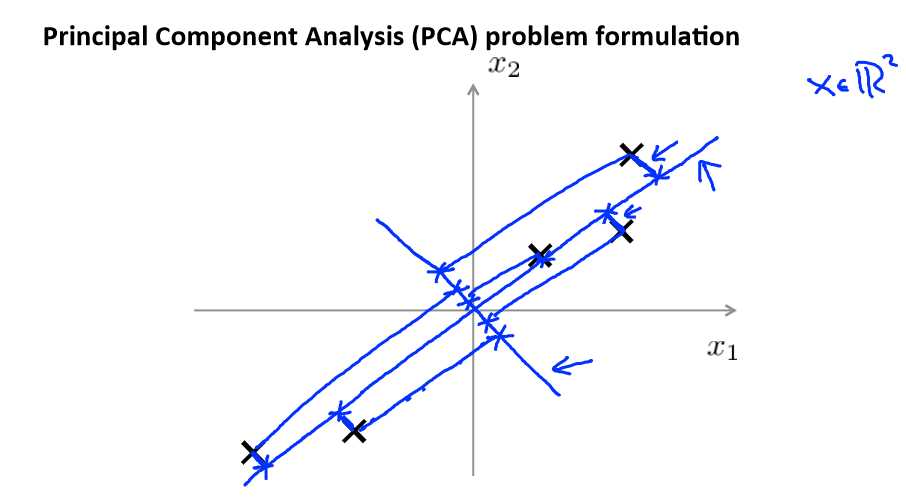
主成分分析（PCA）是最常见的降维算法。 

在 PCA 中，我们要做的是找到一个方向向量（Vector direction），当我们把所有的数据都 投射到该向量上时，我们希望投射平均均方误差能尽可能地小。方向向量是一个经过原
点的向量，而投射误差是从特征向量向该方向向量作垂线的长度。

PCA 技术的一大好处是对数据进行降维的处理，一个很大的优点是，它是完全无参数限制的。但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了

数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。 

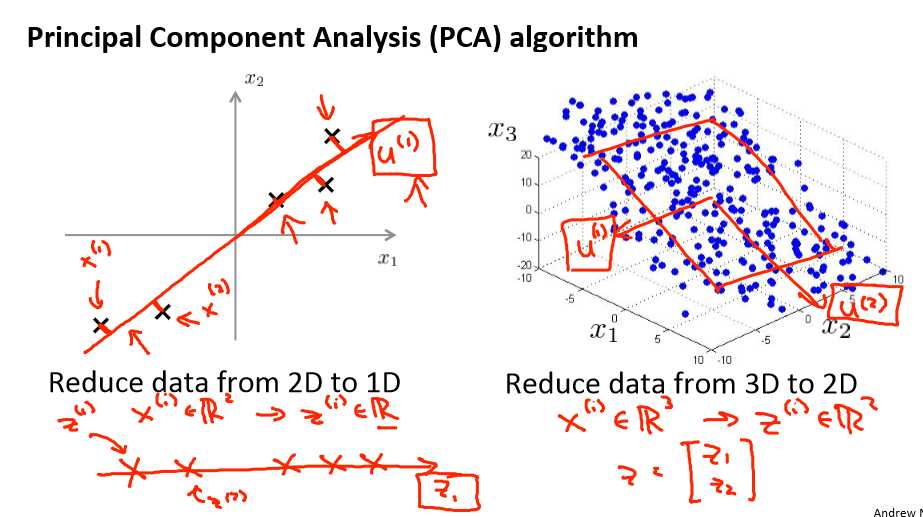
Principal Component Analysis algorithm  

PCA 减少 n 维到 k 维：
第一步是均值归一化。我们需要计算出所有特征的均值，然后令 x_j= x_j -μ_j。如果特征是在不同的数量级上，我们还需要将其除以标准差 σ²。

第二步是计算协方差矩阵（covariance matrix）Σ： 

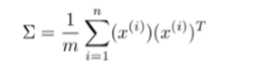
第三步是计算协方差矩阵 Σ 的特征向量（eigenvectors）：

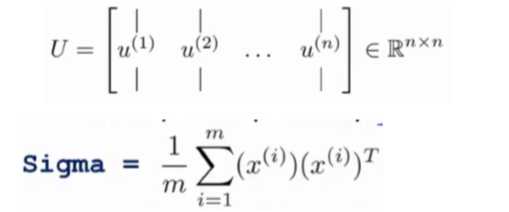
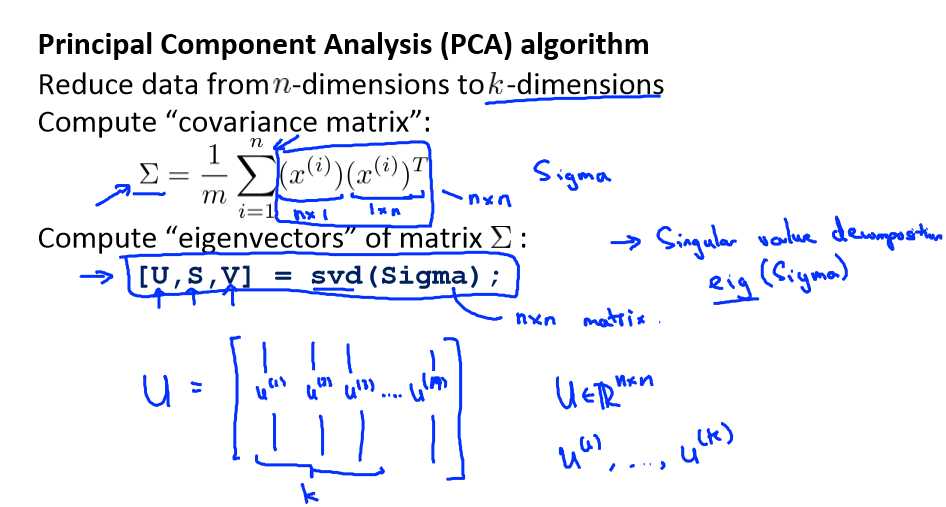
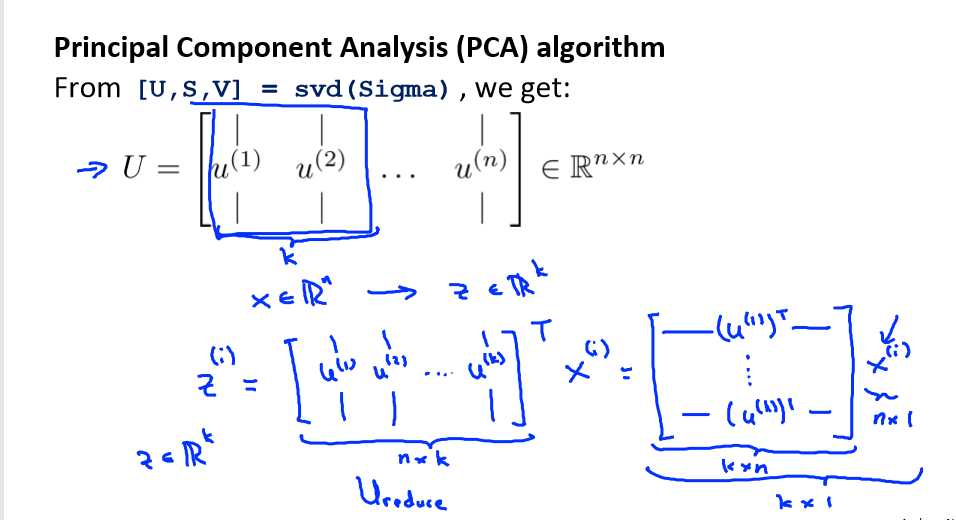
对于一个 n×n 维度的矩阵，上式中的 U 是一个具有与数据之间最小投射误差的方向向量构成的矩阵。

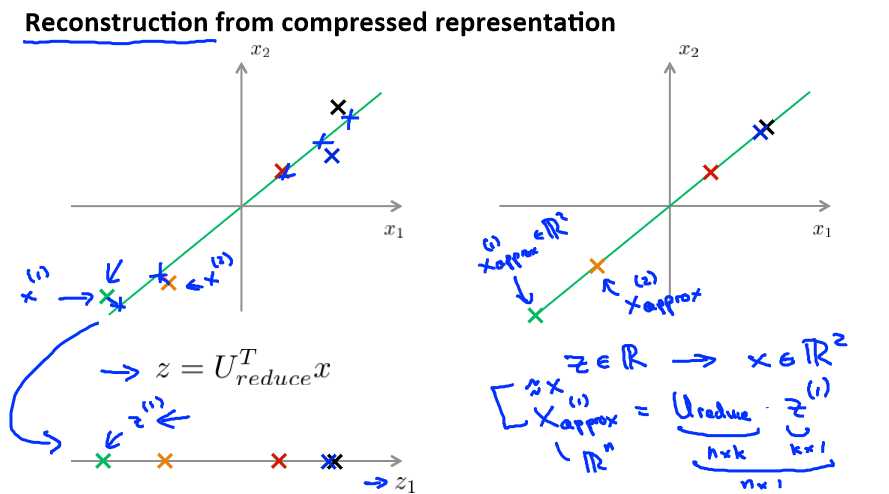
Reconstruction from compressed representation

如果我们希望将数据从 n 维降至 k 维，我们只需要从 U 中选取前 K 个向量，获得一个 n×k 维度的矩阵，我们用 U_reduce 表示，然后通过如下计算获得要求的新特征向量 z⁽ⁱ⁾：

Choosing the number of principal components  

主要成分分析是减少投射的平均均方误差： 

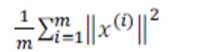
我们可以先令 K=1，然后进行主要成分分析，获得 U_reduce 和 z，然后计算比例是否小于 1%。如果不是的话再令 K=2，如此类推，直到找到可以使得比例小于 1%的最小 K 值（原因是各个特征之间通常情况存在某种相关性）。

还有一些更好的方式来选择 K，当我们在 Octave 中调用“svd”函数的时候，我们获得三个参数：[U, S, V] = svd(sigma)。

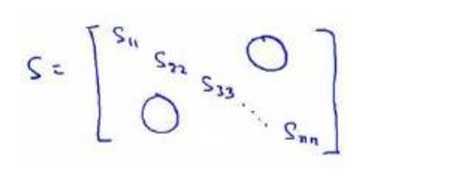
其中的 S 是一个 n×n 的矩阵，只有对角线上有值，而其它单元都是 0，我们可以使用这个矩阵来计算平均均方误差与训练集方差的比例：

在压缩过数据后，我们可以采用如下方法来近似地获得原有的特征： 

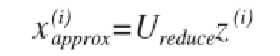
Advice for applying PCA  

假使我们正在针对一张 100×100 像素的图片进行某个计算机视觉的机器学习，即总共有 10000 个特征。
1、第一步是运用主要成分分析将数据压缩至 1000 个特征 

2、然后对训练集运行学习算法 

3、在预测时，采用之前学习而来的 Ureduce 将输入的特征 x 转换成特征向量 z，然后再进行预测

 　　错误的主要成分分析情况：一个常见错误使用主要成分分析的情况是，将其用于减少过拟合（减少了特征的数量）。这样做非常不好，不如尝试归一化处理。原因在于主要成分分析只是近似地丢弃掉一些特征，它并不考虑任何与结果变量有关的信息，因此可能会丢失非常重要的特征。然而当我们进行归一化处理时，会考虑到结果变量，不会丢掉重要的数据。

　　另一个常见的错误是，默认地将主要成分分析作为学习过程中的一部分，这虽然很多时候有效果，最好还是从所有原始特征开始，只在有必要的时候（算法运行太慢或者占用太多内存）才考虑采用主要成分分析。