上一篇博文我们提到了图的最短路径问题:http://www.cnblogs.com/mm93/p/8434056.html。而最短路径问题可以说是这样的一个问题:路已经修好了,该怎么从这儿走到那儿?但是在和图有关的问题中,还有另一种有趣的问题:修路的成本已经知道了,该怎么修路才能尽可能节约成本,同时将这些地方都连起来?
比如我们知道有这么几个城市,它们互相之间还没有路:
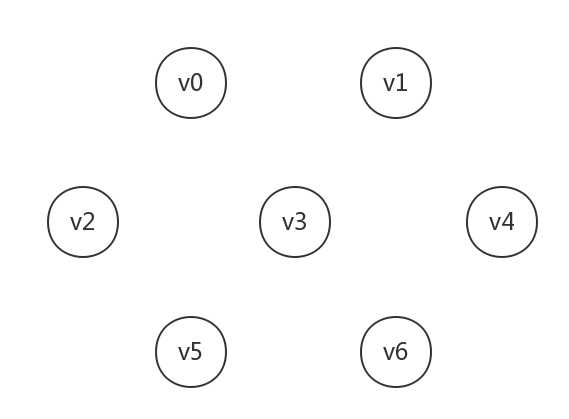
经过实地考察后,发现可以修的路以及各条路的修路成本如下:
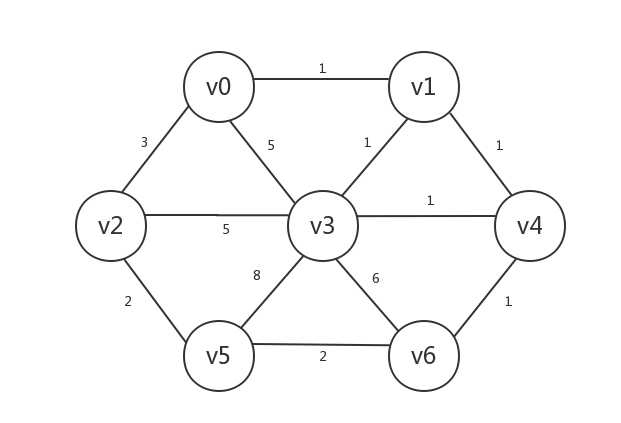
但是我们的预算有限,需要在修路时尽可能的省钱(也就是尽量减小所有边的权重之和),同时保证图中每一个城市总是能到达图中任意一个城市,该怎么修路呢?对于上图来说,其中一个方案是这样的,其总共的修路成本(即总权重)为8:
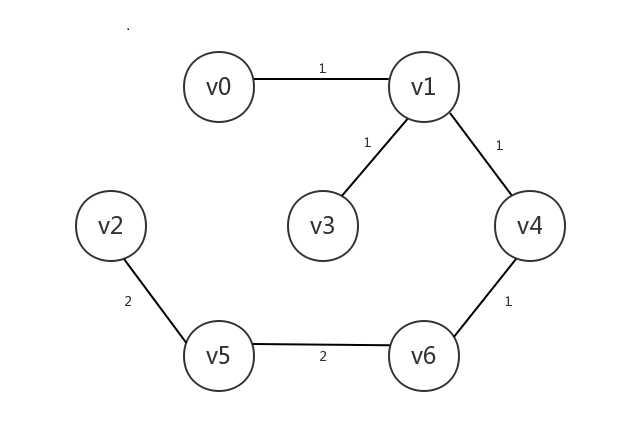
另一个方案是这样的,略有不同,不过总成本也是8:
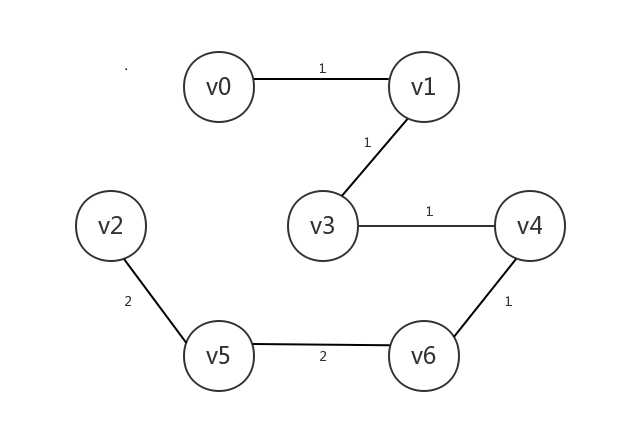
像这样的问题,就是我们今天要讨论的最小生成树问题。为了更准确地说明什么是最小生成树,我们需要先了解一个概念:连通。对于一个无向图而言,如果每个顶点到每个其它顶点都存在路径,则该无向图是连通的。而对于有向图而言,道理相同又稍有变化,在有向图中,若每个顶点到每个其它顶点都存在可行的路径,则该有向图是强连通的。比如下图就不是一个强连通的有向图,其中非v0顶点无法到达v0顶点:
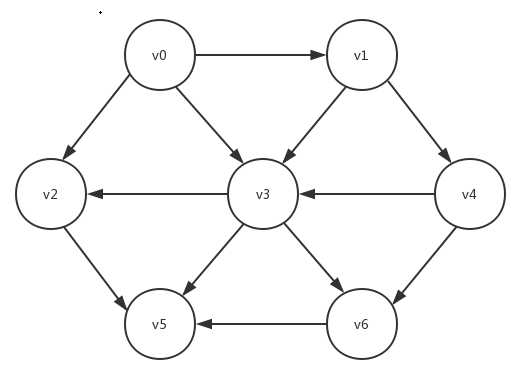
但是如果我们将上面这个有向图的边都变为无向边,我们就会得到一个无向图,此无向图即该有向图的基础图(underlying graph)。如果一个有向图非强连通,但是其基础图是连通的,我们就称该有向图是弱连通的。上面这个有向图就是一个弱连通的有向图。
明白了什么是连通之后,接下来我们说说最小生成树是什么:在一个连通的无向图的所有边中,挑选出足以使所有顶点连通的那些边,且这些边的总权重不能更低,则这些边与所有顶点构成的图就是最小生成树。“最小”的意思是其总权重是最小的,“生成”则是因为这个树是从一个无向图中找出来的,也即生成的。
等等_(:з」∠)_ 不是说“这些边与所有顶点构成的图”吗,怎么就成了树?原因是这样的,如果一个无向图是连通的,那么我们就能找出满足上述条件的那个图,而如果那个图存在,那它一定是一棵树(树是特殊的图嘛,这一点应该要懂的),比如本文前面所找出的最小生成图,显然是一棵树:

为什么称最后找出来的顶点与边的集合为最小生成树,我们已经知道了,而为什么最后找出来的一定是树……咱能不纠结吗 ( ̄. ̄)
好了,接下来讨论下一个问题:有向图可以找出最小生成树吗?答案是可以,只要有向图是强连通的。并且寻找有向图的最小生成树的过程也是基本一样的,因为无向图本就是以有向图的形式存储的(一条无向边拆成两条有向边)。不过因为本文并不打算给出可运行的代码,所以我们的讨论以无向图为基准,主要关注算法的思路,并且不考虑所给图非连通的情况。
想要在图中找出最小生成树,有两种算法可供选择:Prim算法和Kruskal算法。因为Prim算法与寻找最短路径的Dijkstra算法非常非常非常像,所以我们先来讨论一下Prim算法。
Prim算法的思路是这样的:
1.任选一个顶点,将其标为已知,即表示该顶点已在树中(Dijkstra算法中,起点由我们指定)
2.找出所有已知顶点邻接的未知顶点,其中与任一已知顶点的邻接边权重最小的未知顶点,我们将其标为已知,同时将其preV设为与其邻接边最小的已知顶点,且其distance设为该邻接边的权重(在Dijkstra算法中,我们用的是“指向”,因为要考虑到有向图的情况,此外,Dijkstra算法中,我们将被标为已知的未知顶点的distance设为与其相连的已知顶点的distance加上边的权重)
3.反复执行第二步,直至不存在已知顶点邻接了未知顶点为止。
抽象的说,Prim算法就是随机选一个顶点,将其拉进原先为空的树中,然后不断地通过尽可能小的边将其他顶点拉进这棵树中
老样子,上述说法晦涩难懂 ( ̄. ̄)。所以我们需要实际的走一遍来加深一下理解,以下图为例:

假设我们以v3作为起点,则图初始化后的状态如下(顶点旁有红圈表示该顶点已知,红圈中即该顶点的preV,顶点的distance我们暂不考虑):
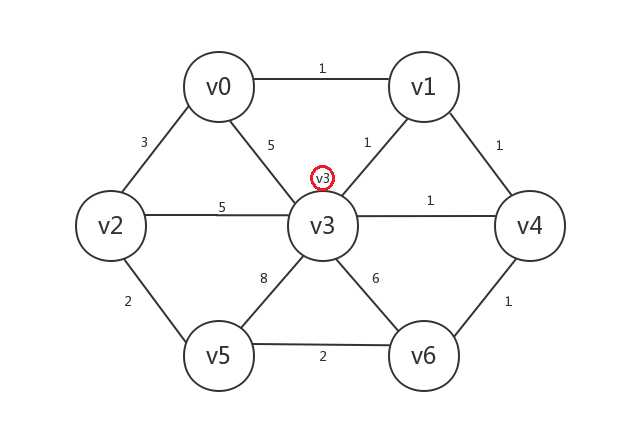
接着,我们找出所有已知顶点(v3)邻接的所有未知顶点:v0、v1、v2、v4、v5、v6。发现与已知顶点邻接边最小的未知顶点是v1、v4,其中未知顶点v1与已知顶点v3的邻接边权重为1,未知顶点v4与已知顶点v3的邻接边权重也为1,我们任选其一即可,比如选择v1,然后将v1设为已知,v1.preV=v3:
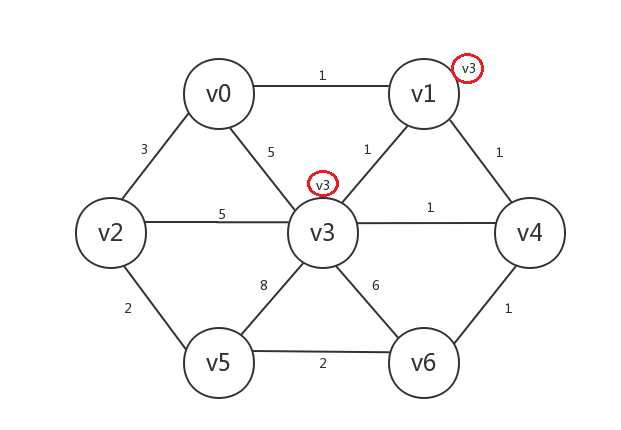
继续,我们找出所有已知顶点(v1、v3)邻接的所有未知顶点:v0、v2、v4、v5、v6,发现与已知顶点邻接边最小的未知顶点是v0、v4,其中未知顶点v0与已知顶点v1的邻接边权重为1,未知顶点v4与已知顶点v1或v3的邻接边权重为1,我们任选其一,比如v4,然后将v4设为已知,v4.preV=v1(也可以是v4.preV=v3):
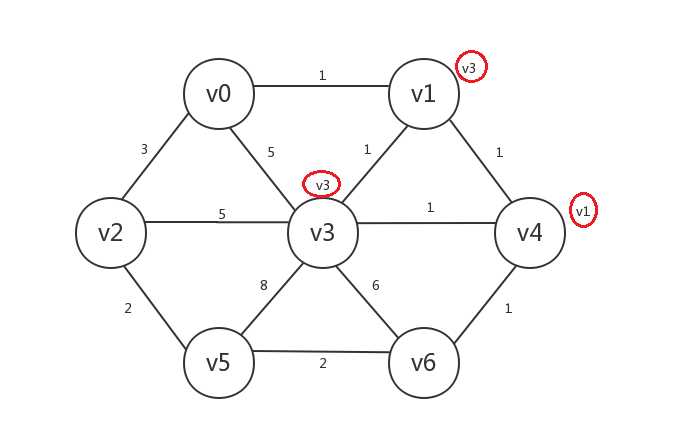
继续,我们找出所有已知顶点(v1、v3、v4)邻接的所有未知顶点:v0、v2、v5、v6,发现与已知顶点邻接边最小的未知顶点是v0、v6,其中未知顶点v0与已知顶点v1的邻接边权重为1,未知顶点v6与已知顶点v4的邻接边权重为1,我们选v6,将v6设为已知,v6.preV=v4:
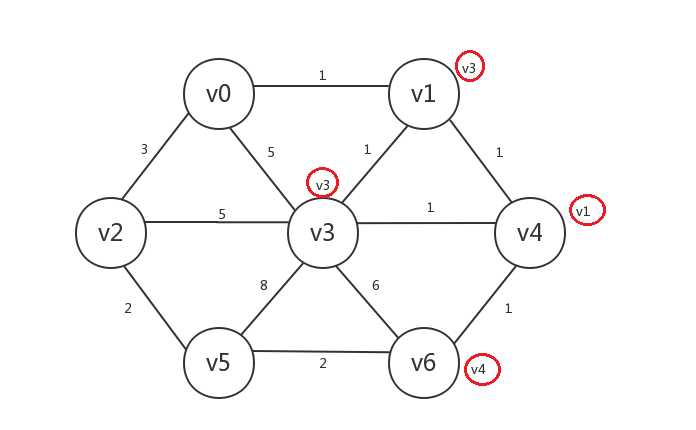
继续,我们找出所有已知顶点邻接的所有未知顶点:v0、v2、v5,其中与已知顶点的邻接边最小的是v0,未知顶点v0与已知顶点v1的邻接边权重为1,我们将v0设为已知,v0.preV=v1:
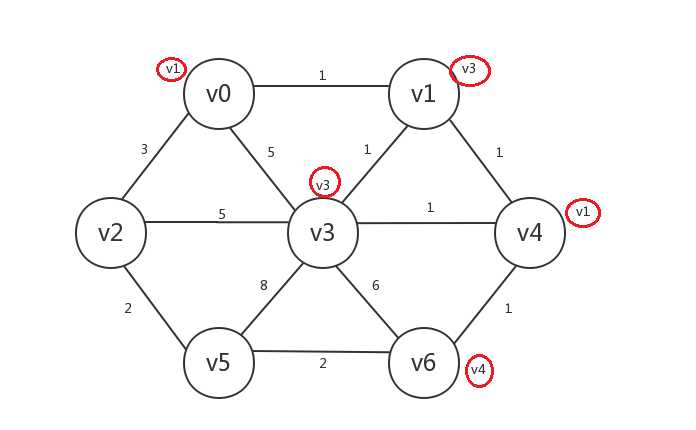
继续,找出所有已知顶点邻接的所有未知顶点:v2、v5,发现其中未知顶点v5与已知顶点v6的邻接边权重最小为2,所以我们将v5设为已知,v5.preV=v6:
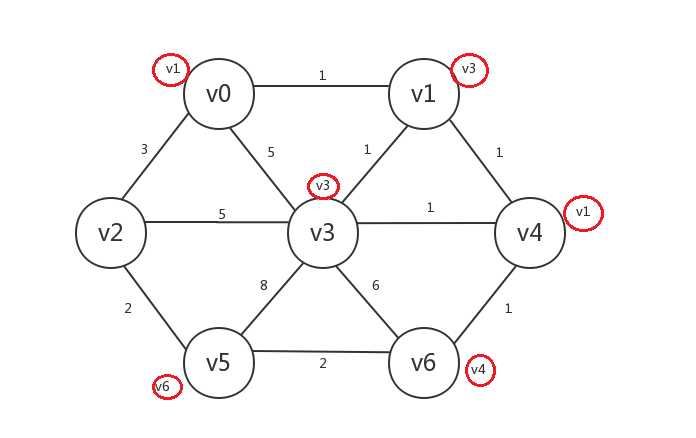
继续,找出所有已知顶点邻接的所有未知顶点:v2,其中未知顶点v2与已知顶点v5的邻接边权重最小,所以我们将v2设为已知,v2.preV=v5:
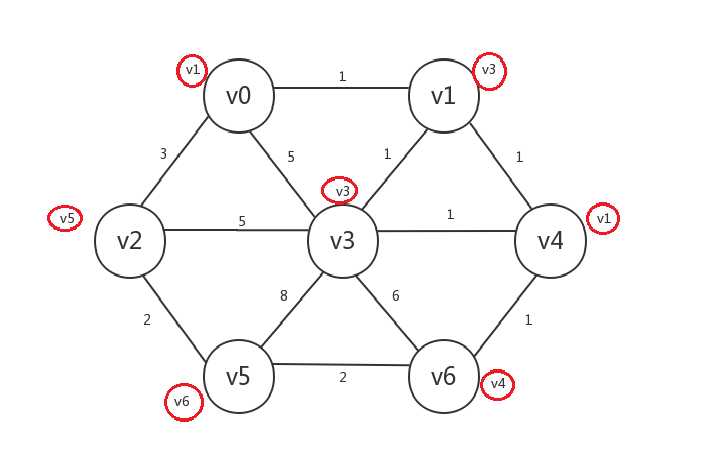
继续,发现已经没有哪个已知顶点邻接了未知顶点,所以算法结束。
接下来,我们只要进行这两步操作就可以得出最小生成树:
1.将每个顶点与其preV相连的边标为已知
2.将非已知的边删去。
将每个顶点与其preV相连的边标为已知(注意,v3的preV是自身,此情况我们不做任何操作即可):
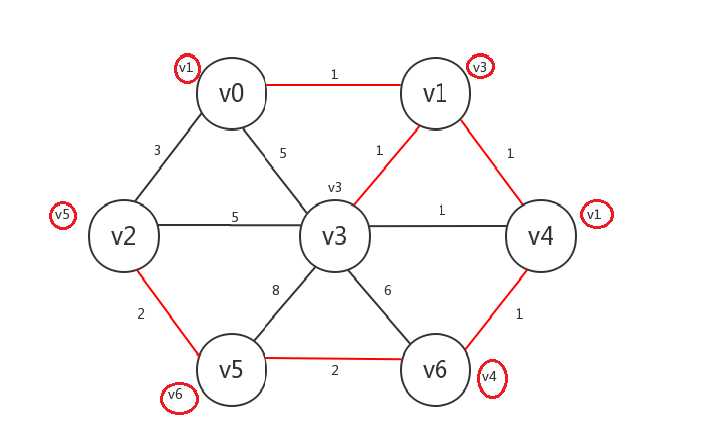
删去非已知的边:
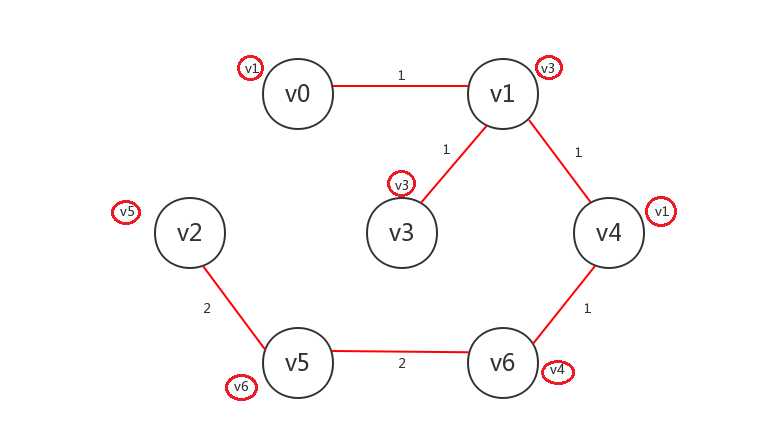
当然,在实际编程中,有可能并不会执行这两个操作,我们只要在将最小生成树的相关信息保存在pathTable中即可,本例中算法结束后pathTable应为如下(与Dijkstra算法使用的pathTable略有不同:没有distance域):
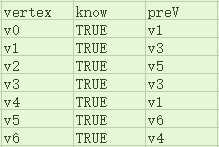
当然,我们也可以使用和Dijkstra算法时一样的pathTable,即加上distance域,不过在计算最小生成树时,一个顶点的distance域应该是其与preV邻接的边的权重:
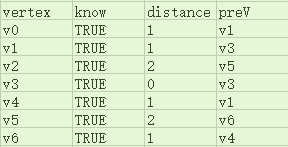
在我们走一遍Prim算法时,我们发现v4.preV既可以设为v3,也可以设为v1,这就已经说明了一点:一个图的最小生成树并不一定是唯一的。不过还要注意的是:一个图即便有多个最小生成树,它们的总权重也应该是一样的。
如果你回顾一遍Prim算法和Dijkstra算法,就会发现,Prim算法与Dijkstra算法的区别可以说就两个:
1.Prim算法的“起点”是任选的,Dijkstra算法是给定的(毕竟要找的是单源最短路径)
2.Prim算法在将一个未知顶点设为已知时,其distance设为其与已知顶点的最小邻接边的weight,而Dijkstra算法则是设为已知顶点.distance+weight
换句话说,Prim算法就是稍稍修改了一下的Dijkstra算法。如果你仔细观察我们用Prim算法生成的树,你会发现从v3出发到任意顶点的路径恰好是v3到该顶点的最短路径:

接下来本应讨论Kruskal算法,但是我忽然发现我之前忘了写一篇关于树的集合与不相交集的博文(⊙?⊙)。如果要讨论Kruskal算法,这两个预备知识是必不可少的,而如果这两个知识也要讲解的话,博文就太长了Orz。所以我只简单说说Kruskal的思路。
在Prim算法中,我们是以已知顶点(即已在最小生成树中的顶点)为基础,不断地将未知顶点拉进树中。而Kruskal算法则是另一种思路:以当前最小的边为基础,不断地将未知顶点拉进树中(这个过程可能产生多棵树)。
以下图为例,我们走一遍Kruskal算法:

首先,我们需要将边按权重从小到大排序,才能找“当前最小边”:

先是处理当前最小边[v0,v1],其所连接的两个顶点均未知,所以我们将它们均设为已知,并连起来:
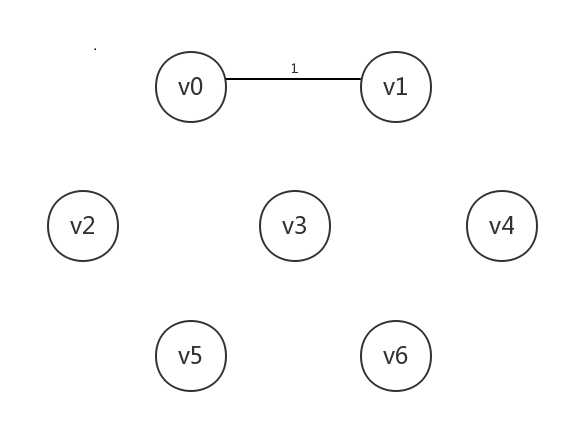
然后处理下一个当前最小边[v1,v3],其所连接的v3未知,将v3设为已知,连起来:
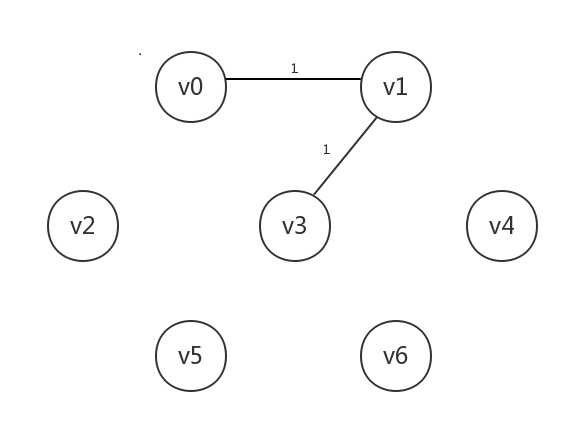
接着处理边[v3,v4],其连接的v4未知,将v4设为已知,连起来:
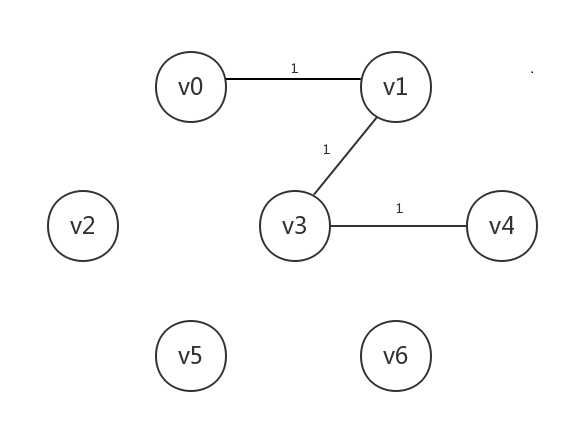
接着处理边[v1,v4],其连接的两个顶点均为已知,故跳过
接着处理边[v4,v6],其连接的v6未知,将v6设为已知,连起来:
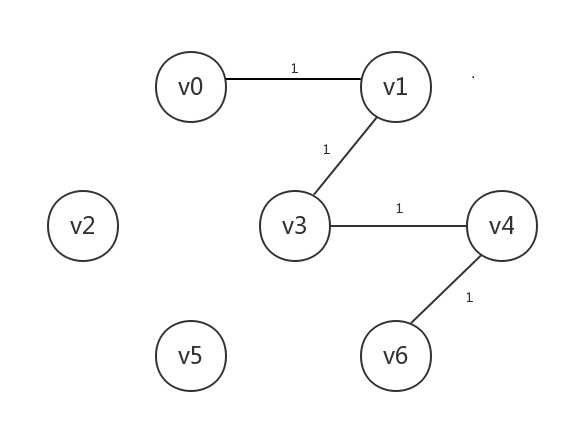
接着处理边[v2,v5],其连接的v2和v5均为未知,所以将v2、v5均设为已知,连起来(注意,此时产生了两棵树):
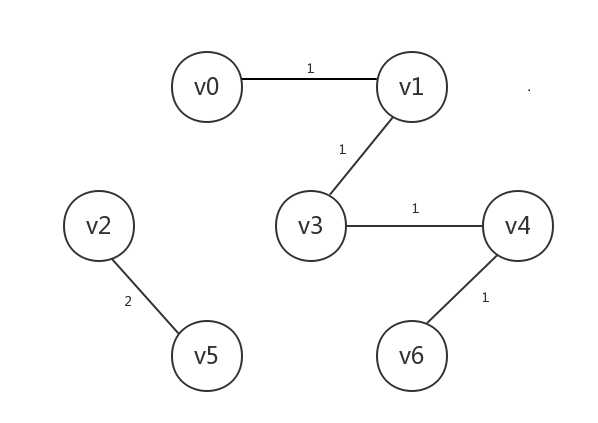
接着处理边[v5,v6],其连接的顶点均为已知,但是v5和v6处于不同的树,所以我们将其连起来(这部分的相关判断和处理需要树的集合知识,以及不相交集数据结构):
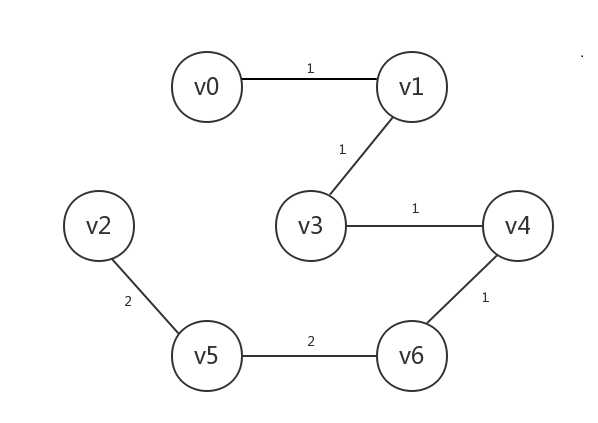
接下来处理的所有边都是所连接顶点已知,且所连接顶点处于同一棵树中,所以均会跳过,然后算法结束。
没有掌握住博文的顺序和铺垫,实在是失败 ̄△ ̄
不过Kruskal算法的思路我想我应该讲清楚了,就是Dijkstra算法和Prim算法的讲解可能太生硬了一些,但是细细地读、细细地理解、细细地过一遍,应该还是能明白的?ω?
这个系列的博文的主体部分到这儿就算结束了,从第一篇博文一路看到这儿的话,基本的数据结构和算法应该都能掌握。而像什么B+树、红黑树、算法设计技巧等更特殊的知识我没有算在主体部分中,以后可能会以“浅入浅出数据结构(附)”的标题形式写出。
