一、左旋
1、当在含有n个关键字的红黑树上运行时,TREE-INSERT和TREE-DELETE操作对树作了修改,结果可能违反(一、红黑树--》2、定义)中给出的红黑树的性质,为了保持这些性质,就要改变树中的某些节点的颜色以及指针结构。
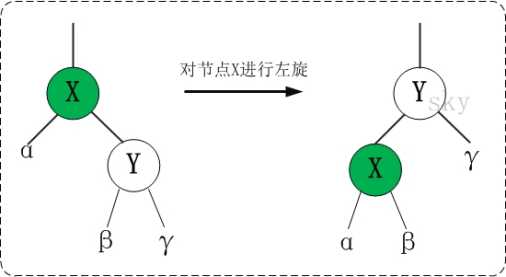
对x进行左旋,意味着"将x变成一个左节点"。左旋以x到y之间的链为“支轴”进行。它使y成为该子树新的根,x成为y的左孩子,y的左孩子成为x的右孩子。
2、伪代码:在LEFT-ROTATE得伪代码中,假设right[x]!=nil[T]
1 LEFT-ROTATE(T, x) 2 y ← right[x] // 前提:这里假设x的右孩子为y。下面开始正式操作 3 right[x] ← left[y] // 将 “y的左孩子” 设为 “x的右孩子”,即 将β设为x的右孩子 4 p[left[y]] ← x // 将 “x” 设为 “y的左孩子的父亲”,即 将β的父亲设为x 5 p[y] ← p[x] // 将 “x的父亲” 设为 “y的父亲” 6 if p[x] = nil[T] 7 then root[T] ← y // 情况1:如果 “x的父亲” 是空节点,则将y设为根节点 8 else if x = left[p[x]] 9 then left[p[x]] ← y // 情况2:如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” 10 else right[p[x]] ← y // 情况3:(x是它父节点的右孩子) 将y设为“x的父节点的右孩子” 11 left[y] ← x // 将 “x” 设为 “y的左孩子” 12 p[x] ← y // 将 “x的父节点” 设为 “y”
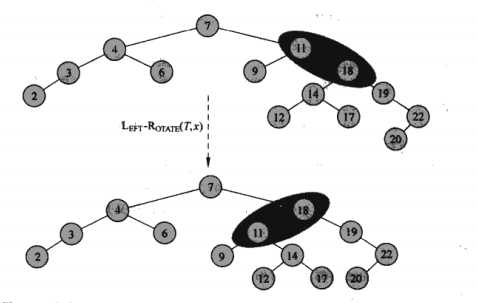
3、Right-ROTATE与LEFT-ROTATE的程序是对称的。他们都是在O(1)时间内执行的。旋转只有指针被改变;而节点中所有其他域都保持不变。
