背包问题是一类经典的动态规划问题,本节只介绍两类最简单的背包问题:01 背包问题和完全背包问题。
一、多阶段动态规划问题
有一类动态规划可解的问题,它可以描述成若干个有序的阶段,且每个阶段的状态只和上一阶段的状态有关,一般把这类问题称为多阶段动态规划问题。如下图所示,该问题被分为 5 个阶段,其中状态 F 属于阶段 3,它由状态 2 的状态 C 和状态 D 推得。01 背包问题就是这样一个例子。
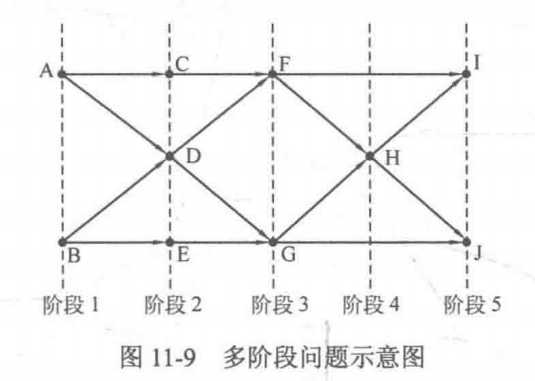
二、01 背包问题
01 背包问题是这样的:

下面介绍动态规划的方法。
令 dp[i][v] 表示前 i 件物品 (1≤i≤n, 0≤v≤V) 恰好装入容量为 v 的背包中所能获得的最大价值。考虑对第 i 件物品的选择策略,有两种策略:
- 不妨第 i 件物品,那么问题转化为前 i-1 件物品恰好装入容量为 v 的背包中所能获得最大价值,也即 dp[i-1][v]。
- 放第 i 件物品,那么问题转化为前 i-1 件物品恰好装入容量为 v-w[i] 的背包中所能获得的最大价值,也即 dp[i-1][v-w[i]] + c[i]。
由此可以写出状态转移方程:
$dp[i][v]=max\left \{ dp[i-1][v], dp[i-1][v-w[i]]+c[i] \right \}$
$1\leqslant i\leqslant n,w[i]\leqslant v\leqslant V$
注意到 dp[i][v] 只与之前的状态 dp[i-1][] 有关,所以可以枚举 i 从 1 到 n ,v 从 0 到 V,通过边界 dp[0][v](0≤v≤V)(即前 0 件物品放入任何容量 v 的背包中都只能获得价值 0)就可以把整个 dp 数组递推出来。而由于 dp[i][v] 表示的是恰好为 v 的情况,所以需要枚举 dp[n][v](0≤v≤V),取最大值才是最后的结果。
代码如下:
1 int i, v; 2 for(i=1; i<=n; ++i) { 3 for(v=w[i]; v<=V; ++v) { 4 dp[i][v] = max(dp[i-1][v], dp[i-1][v-w[i]]+c[i]); 5 } 6 }
此时时间复杂度和空间复杂度都为 O(nV),空间复杂度还可以再优化。
注意到状态转移方程中计算 dp[i][v] 时总是只需要 dp[i-1][v] 左侧部分的数据,因此可以直接开一个一维数组 dp[v],枚举方向改变为 i 从 1 到 n, v 从 V 到 0(逆序!),这样状态转移方程为:
$dp[v]=max(dp[v],dp[v-w[i]]+c[i])$
$1\leqslant i\leqslant n,w[i]\leqslant v\leqslant V$
代码如下:
1 int i, v; 2 // 滚动数组形式 3 for(i=1; i<=n; ++i) { 4 for(v=V; v >= w[i]; --v) { // 逆序枚举 v 5 dp[v] = max(dp[v], dp[v-w[i]] + c[i]); 6 } 7 }
特别说明:如果用二维数组存放,v 的枚举是顺序还是逆序都无所谓;如果使用一维数组存放,则 v 的枚举必须是逆序!
完整的求解 01背包问题的代码如下:
1 /* 2 01背包问题 3 */ 4 5 #include <stdio.h> 6 #include <string.h> 7 #include <math.h> 8 #include <stdlib.h> 9 #include <time.h> 10 #include <stdbool.h> 11 12 #define maxn 100 13 #define maxv 1000 14 int w[maxn], c[maxn], dp[maxv]; 15 16 // 求较大值 17 int max(int a, int b) { 18 return (a>b ? a : b); 19 } 20 21 int main() { 22 int i, v, n, V; 23 scanf("%d %d", &n, &V); 24 for(i=1; i<=n; ++i) { 25 scanf("%d", &w[i]); // 输入物品重量 26 } 27 for(i=1; i<=n; ++i) { 28 scanf("%d", &c[i]); // 输入物品价值 29 } 30 // 边界 31 for(v=0; v <= V; ++v) { 32 dp[v] = 0; 33 } 34 // 状态转移方程 35 for(i=1; i<=n; ++i) { 36 for(v=V; v >= w[i]; --v) { // 逆序枚举 v 37 dp[v] = max(dp[v], dp[v-w[i]] + c[i]); 38 } 39 } 40 // 寻找最大值即为答案 41 int maxc = 0; 42 for(v=0; v<=V; ++v) { 43 if(dp[v] >= maxc) { 44 maxc = dp[v]; 45 } 46 } 47 printf("%d\n", maxc); // 输出 48 49 return 0; 50 }
另外,01背包中的每个物品都可以看作一个阶段,这个阶段中的状态有 dp[i][0]~dp[i][v],它们均由上一个阶段的状态得到。事实上,对能够划分阶段的问题来说,都可以尝试把阶段作为状态的一维,这可以使我们更方便地得到无后效性的状态。从中也可以得到这么一个技巧,如果当前设计的状态不满足无后效性,那么不妨把状态进行升维,即增加一维或若干维来表示相应的消息,这样可能就能满足无后效性。
三、完全背包问题
完全背包问题的叙述如下:
同样令 dp[i][v] 表示前 i 件物品恰好放入容量为 v 的背包中能获得的最大价值。和 01背包问题一样,考虑对第 i 件物品的选择策略,有两种策略:
- 不放第 i 件物品,那么 dp[i][v] = dp[i-1][v]。
- 放第 i 件物品。这里的处理与 01背包问题有所不同,完全背包问题如果选择放第 i 件物品之后并不是转移到 dp[i-1][v-w[i]] 这个状态,而是转移到 dp[i][v-w[i]],这是因为每种物品可以放任意件,放了第 i 件物品后还可以继续放第 i 件物品,直到第二维的 v-w[i] 无法保持大于等于 0 为止。
因此可以写出状态转移方程:
$dp[i][v]=max\left \{ dp[i-1][v], dp[i][v-w[i]]+c[i] \right \}$
$1\leqslant i\leqslant n,w[i]\leqslant v\leqslant V$
边界:dp[0][v]=0(0≤v≤V)
而这个状态转移方程同样可以改写成一维形式,即状态转移方程:
$dp[v]=max(dp[v],dp[v-w[i]]+c[i])$
$1\leqslant i\leqslant n,w[i]\leqslant v\leqslant V$
边界:dp[v]=0(0≤v≤V)
写成一维形式之后和 01背包完全相同,唯一的区别在于这里 v 的枚举顺序是正向枚举,而 01背包的一维形式中 v 必须是逆向枚举。代码如下:
1 int i, v; 2 for(i=1; i<=n; ++i) { 3 for(v=w[i]; v <= V; ++v) { // 正向枚举 v 4 dp[v] = max(dp[v], dp[v-w[i]]+c[i]); 5 } 6 }
