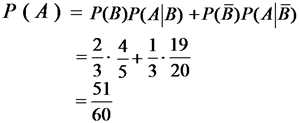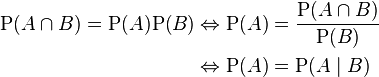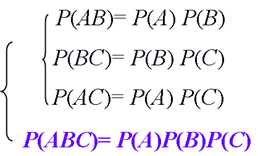原创地址:?http://www.cnblogs.com/Alandre/?(泥沙砖瓦浆木匠),须要转载的,保留下! Thanks

? ? ? ?加油! 大牛总是不断努力,你却更须要加倍努力.

Written In The Font

??? 数学和生活是技术之本, 有了数学,加上生活,才会开心.

??? 今天继续概率论:

• 全概率
• 贝叶斯
• 事件独立性

Content

The total probability

In the Set :
?????

?????????????????????????????????????????????????????????????

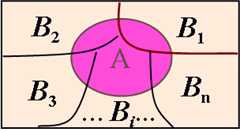
The law of?total probability?is the proposition that if?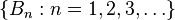?is a finite or countably infinitepartition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event??is?measurable, then for any event??of the same probability space:

?????????????

example:

例. 甲、乙两家工厂生产某型号车床，当中次品率分别为20%, 5%。已知每月甲厂生产的数量是乙厂的两倍，现从一个月的产品中随意抽检一件，求该件产品为合格的概率？

设A表示产品合格，B表示产品来自甲厂

?

Bayes

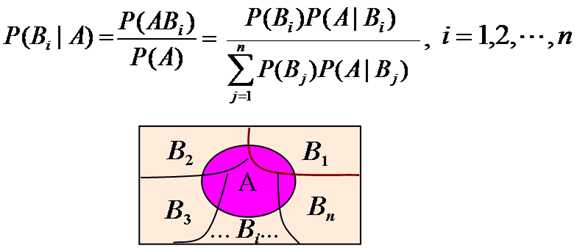
for some partition {B_j} of the event space, the event space is given or conceptualized in terms of?P(B_j) and?P(A|B_j). It is then useful to compute?P(A)?using the law of total probability:????????

???????????????????????????????

?

example:

An entomologist spots what might be a rare subspecies of beetle, due to the pattern on its back. In the rare subspecies, 98% have the pattern, or?P(Pattern|Rare)?= 98%. In the common subspecies, 5% have the pattern. The rare subspecies accounts for only 0.1% of the population. How likely is the beetle having the pattern to be rare, or what is?P(Rare|Pattern)?

From the extended form of Bayes‘ theorem (since any beetle can be only rare or common),

?

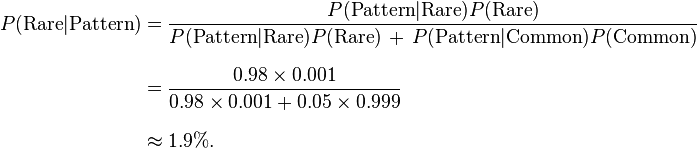
One more example:

?

Independence

Two events

Two events?A?and?B?are?independent?if and only if their joint probability?equals?the product of their probabilities:

.

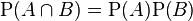Why this defines?independence?is made clear by rewriting with?conditional?probabilities:

how about Three events

???????????

?

sometimes , we will see the Opposition that can be used to make the mess done. We will use the rule of independence such as :?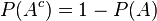

?

Editor‘s Note

“学吧,至少不亏.”一句良言 终身受用.