hdu 5033 buiding(单调栈)
某年某月某天,马特去了一个小镇。这个小镇如此狭窄,以至于他可以把小镇当作一个枢纽。在镇上有一些摩天大楼,其中一栋位于xi,高度为hi。所有的摩天大楼位于不同的地方。为了简化题目,假设摩天大楼没有宽度。由于摩天大楼如此之高,马特几乎看不到天空。对于马特所在的位置,他想知道他能看到天空的角度范围有多大。假设马特的身高是0。可以保证,对于每个查询,马特的左右两边至少有一座建筑物,而且他的位置上没有建筑物。建筑物的数量n<1e5,查询次数Q<1e5。
我用常规思路,想不出什么好方法。既然这道题的普遍解法是单调栈,那么我们就来看一下单调栈怎么实现。首先,单调队列和单调栈的前提是,加入的元素满足一种有序的关系。所以我们自然而然地就想到,将所有查询排序,从左向右和从右向左分别进行查询的计算。以从左向右为例,如何做到在(均摊)O1的时间内找到一个查询的答案呢?我们先来找些性质。
性质1:如果一个建筑物i比它左侧的j高,那么当i和j都在马特左侧时,马特一定看不到j。也就是说,如果维护一个关于建筑物下标的单调栈,新加进来一个建筑时,可以把它左侧所有更矮的建筑删掉。那么,现在的单调栈就是单调递减的。这就去除了第一种冗余状态。
性质2:从左向右而言,如果有这样的情况:
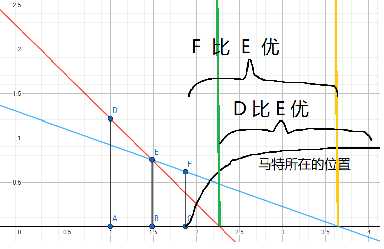
,也就是单调栈中的顶上两个建筑和新加进来的建筑组成一个凹包(不好意思,下凸包),那么可以直接把单调栈顶的建筑删了,一直循环删下去。因为无论马特怎么站,都不会被它挡住。第二种冗余状态也被我们去除了。那么现在,单调栈存储的建筑就组成了一个上凸包。
性质3:然而,优化力度还不够大。这样子算法依然不是O(n)的。那怎么办呢?

由于马特一直往右跑,那么他与凸包相切的点只会往左移动:
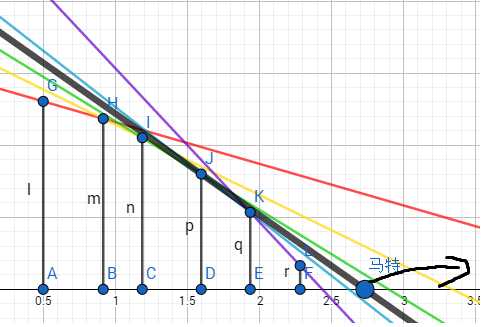
所以,在加入新的建筑之后,判断一下马特与当前凸包的交点,然后将交点右侧的建筑全删了(弹出)即可。栈顶的建筑就是最优建筑(切线嘛)。这就去除了第三种冗余状态。然而这样的时间复杂度是均摊O(1)的吗?额,显然的。
这可能是目前为止我写的最详细的一篇博文。。
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=1e5+5;
const double pi=3.1415926535898;
struct stack{
int t, a[maxn];
void push(int x){ a[++t]=x; }
void pop(){ if (--t==-1) ++t; }
void reset(){ t=0; }
inline int top(){ return a[t]; }
inline int top2(){ return a[t-1]; }
}s;
struct query{
int id, ans1, ans2; double x;
}q[maxn], q2[maxn];
struct building{
double x, h;
}b[maxn];
int n, T, Q;
bool cmp1(query &a, query &b){
return a.x<b.x; }
bool cmp2(query &a, query &b){
return a.id<b.id; }
bool cmpb(building &a, building &b){
return a.x<b.x; }
double angle(double x, double y){
return atan(x/y)*180/pi;
}
int main(){
scanf("%d", &T); int tmp=0;
while (T--){
++tmp; s.reset();
scanf("%d", &n);
for (int i=1; i<=n; ++i)
scanf("%lf%lf", &b[i].x, &b[i].h);
scanf("%d", &Q);
for (int i=1; i<=Q; ++i){
scanf("%lf", &q[i].x);
q[i].id=i;
}
sort(b+1, b+n+1, cmpb);
sort(q+1, q+Q+1, cmp1);
int nowbui=1; s.push(1);
for (int i=1; i<=Q; ++i){
while (b[nowbui+1].x<q[i].x){ //从左到右加入建筑物
++nowbui;
//第一种冗余状态:左边的楼比右边的矮
while (s.t>0&&b[s.top()].h<=b[nowbui].h) s.pop();
//所以现在这个建筑物序列严格下降
//第二种冗余状态:是个下凸函数
while (s.t>1&&(b[nowbui].h-b[s.top()].h)/
(b[nowbui].x-b[s.top()].x)>=
(b[s.top()].h-b[s.top2()].h)/
(b[s.top()].x-b[s.top2()].x)) s.pop();
//所以现在这个建筑物序列是凸包了
s.push(nowbui);
}
//第三种冗余状态:若一栋楼在视线所切的那栋楼的右边,则可以删去
//可以用均摊,证明这里的复杂度是常数
while (s.t>1&&(b[s.top2()].h)/(q[i].x-b[s.top2()].x)>
(b[s.top()].h)/(q[i].x-b[s.top()].x)) s.pop();
//现在终于不仅排除了冗余状态,并且找到了最优解。
q[i].ans1=s.top();
} //从右往左也一样
nowbui=n; s.reset(); s.push(n);
for (int i=Q; i>=1; --i){
while (b[nowbui-1].x>q[i].x){
--nowbui;
//右边的楼比左边的矮
while (s.t>0&&b[s.top()].h<=b[nowbui].h) s.pop();
//下面有图 (其实这里封装一个关于斜率的函数会更好)
while (s.t>1&&(b[nowbui].h-b[s.top()].h)/
(b[nowbui].x-b[s.top()].x)<=
(b[s.top()].h-b[s.top2()].h)/
(b[s.top()].x-b[s.top2()].x)) s.pop();
s.push(nowbui);
}
//下面有图
while (s.t>1&&b[s.top2()].h/(b[s.top2()].x-q[i].x)>
b[s.top()].h/(b[s.top()].x-q[i].x)) s.pop();
q[i].ans2=s.top();
}
sort(q+1, q+Q+1, cmp2);
printf("Case #%d:\n", tmp);
for (int i=1; i<=Q; ++i){
printf("%.5lf\n", 180-angle(b[q[i].ans1].h,
q[i].x-b[q[i].ans1].x)-angle(b[q[i].ans2].h,
b[q[i].ans2].x-q[i].x));
}
}
// printf("%.6lf", angle(1, 1));
return 0;
}