补题进度:8/10
A(计数+BIT)
题意:
给一个长度为n的数组a[],任意选0<=i<=j<n,将a[i]~a[j]从小到大排序,形成新的数组。问有多少个不同的新数组。
N,a[i]<=1000000
分析:
对答案有贡献的ij一定是a[i]不是i~j的最小值,a[j]不是i~j的最大值,于是我们就去统计这样区间的数量
我们用单调栈搞出r[i]表示i右边第一个比a[i]小的位置,l[i]表示i左边第一个比a[i]大的位置
枚举区间左端点,那么可行的右区间在[r[i],n]中,然后我们只需要统计其中有多少位置的l[j]>=i就行了
这个可以离线+BIT解决
B(并查集维护基环外向树森林)
题意:
一个长度为n的01数组,最初都是0,有m个颜色,每个位置有两种染色选择,每种颜色只可以染一次。现在你需要找出一个染色方案满足:
1、被染色的位置数量尽可能多
2、在1的前提下,若用1表示该位置被染,用2表示该位置没被染,你需要让这个字典序尽量大
3、在2的前提下,一个位置如果被染那么它要么是1要么是2(表示染了第一种备选颜色还是第二种),你需要让这个字典序尽量小
n,m<=5*10^5
分析:
如果是问最多染色的个数,那显然只需要维护一下基环外向树森林就行了
现在要输出方案,我们发现第2个条件其实就是让我们尽可能优先用先读入的边,这个在我们维护基环外向树森林的时候就成功处理了
第三个条件其实是让我们考虑最后的基环树/树的染色分配
首先对于基环树,只有环上的有两种选择,树边是定死的,我们只需要枚举两种情况即可
对于树,我们贪心来看,取出id最小的边,令其为1,按照方向去dfs涂色,再取出id次小的边,以此类推……

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e6,inf=1e7; 4 int ans[maxn+5],l[maxn+5],r[maxn+5]; 5 int f[maxn+5]; 6 bool c[maxn+5],incircle[maxn+5]; 7 bool vis[maxn+5]; 8 int n,m,len,top; 9 vector<int> circle,E; 10 struct edge 11 { 12 int from,to,id; 13 }e[maxn*2+5]; 14 int head[maxn+5],nx[maxn+5]; 15 int s[maxn+5]; 16 bool use[maxn*2+5]; 17 void addedge(int u,int v,int id) 18 { 19 ++len; 20 e[len]={u,v,id}; 21 nx[len]=head[u]; 22 head[u]=len; 23 ++len; 24 e[len]={v,u,id}; 25 nx[len]=head[v]; 26 head[v]=len; 27 } 28 int find(int x) 29 { 30 if(f[x]==x) return x;else return f[x]=find(f[x]); 31 } 32 void dfs(int k) 33 { 34 if(vis[k]) 35 { 36 int now=top; 37 circle.push_back(s[now]); 38 --now; 39 while(now>=1&&e[s[now]].to!=k) circle.push_back(s[now--]); 40 return; 41 } 42 vis[k]=1; 43 for(int i=head[k];i!=-1;i=nx[i]) 44 { 45 if(use[i]) continue; 46 edge u=e[i]; 47 s[++top]=i; 48 use[i]=use[i^1]=1; 49 dfs(u.to); 50 --top; 51 } 52 } 53 void paint(int k,int fa) 54 { 55 for(int i=head[k];i!=-1;i=nx[i]) 56 { 57 edge u=e[i]; 58 if(u.to==fa||incircle[u.to]) continue; 59 if(k==l[u.id]) ans[u.id]=2;else ans[u.id]=1; 60 paint(u.to,k); 61 } 62 } 63 void workcircle() 64 { 65 for(int i=0;i<circle.size();++i) incircle[e[circle[i]].to]=1; 66 for(int i=0;i<circle.size();++i) paint(e[circle[i]].to,0); 67 int minid=n+1; 68 for(int i=0;i<circle.size();++i) 69 { 70 edge u=e[circle[i]]; 71 if(u.to==l[u.id]) ans[u.id]=1;else ans[u.id]=2; 72 minid=min(minid,u.id); 73 } 74 if(ans[minid]==2) 75 for(int i=0;i<circle.size();++i) ans[e[circle[i]].id]=3-ans[e[circle[i]].id]; 76 } 77 void dfs1(int k,int fa) 78 { 79 for(int i=head[k];i!=-1;i=nx[i]) 80 { 81 edge u=e[i]; 82 if(u.to==fa) continue; 83 E.push_back(i); 84 dfs1(u.to,k); 85 } 86 } 87 bool cmp(const int x,const int y) 88 { 89 return e[x].id<e[y].id; 90 } 91 void worktree(int start) 92 { 93 E.clear(); 94 dfs1(start,0); 95 sort(E.begin(),E.end(),cmp); 96 for(int i=0;i<E.size();++i) 97 { 98 edge u=e[E[i]]; 99 if(ans[u.id]) continue; 100 ans[u.id]=1; 101 if(u.to==l[u.id]) paint(u.to,u.from);else paint(u.from,u.to); 102 } 103 } 104 int main() 105 { 106 int size = 256 << 20; // 256MB 107 char *p = (char*)malloc(size) + size; 108 __asm__("movl %0, %%esp\n" :: "r"(p)); 109 freopen("ce.in","r",stdin); 110 freopen("ce.out","w",stdout); 111 scanf("%d%d",&n,&m); 112 for(int i=1;i<=m;++i) f[i]=i,head[i]=-1; 113 len=-1; 114 for(int i=1;i<=n;++i) 115 { 116 scanf("%d%d",&l[i],&r[i]); 117 int u=find(l[i]),v=find(r[i]); 118 if(c[u]&&c[v]) continue; 119 if(u!=v) f[u]=v,c[v]|=c[u]; 120 else 121 if(!c[u]&&!c[v]) f[u]=v,c[v]=1; 122 else continue; 123 addedge(l[i],r[i],i); 124 } 125 for(int i=1;i<=m;++i) 126 if(!vis[i]) 127 { 128 circle.clear(); 129 top=0; 130 dfs(i); 131 if(!circle.empty()) workcircle(); 132 else worktree(i); 133 } 134 for(int i=1;i<=n;++i) printf("%d",ans[i]); 135 return 0; 136 }
C(计数+线段树)
题意:
给出一个长度为n的数组a[],问有多少对(x,y)满足:
1、0<=x<=y<n
2、任意i∈[x,y] & j∉[x,y],有a[i]≠a[j]
n<=1000000
分析:
直观来讲,我们是要找区间[x,y]使得颜色被分开了
我们把同样的颜色提取出来,那么对于每个位置我们都能方便的求出l[i],r[i]表示a[i]这个颜色最左边在哪,最右边在哪
那么x只能是一个颜色的起点,y只能是一个颜色的终点
我们去枚举y,计算有多少个合法的x
即要满足max{r[x],r[x+1],...,r[y]}<=y 且 min{l[x],l[x+1],...,l[y]}>=x
那么对于每个y,我们可以用线段树求出最左边的x满足max{r[x],r[x+1],...,r[y]}<=y,记为posl[y]
对于每个x,我们可以用线段树求出最右边的y满足min{l[x],l[x+1],...,l[y]}>=x,即为posr[x]
那么我需要找出[posl[y],y]里面有多少少符合题意的x,即那些posr[x]>=y的x,一眼直接用可持久化线段树支持询问
但仔细分析会发现这样的posr[x]是单减的,所以同样只需要用线段树找出那个分界就行了
D(组合计数)
略
E(构造)
题意:
给你一颗n个点的二叉树,你需要给每个点重新编号1~n使得{fa[2],fa[3],fa[4],...,fa[n]}这个序列字典序最小
n<=2e5
分析:
显然是用bfs的顺序给每个点重新编号,但主要矛盾点就是某个点有两个孩子,两个孩子谁先编号的问题
显然贪心选择这两个孩子当中size最大的那个
若这两个孩子的size又相同呢……?
那么再比较这两个孩子的孩子……这样深入下去
这样时间复杂度能保证吗?看似是O(n^2)的啊
每次考察一个点u,向下需要一直深入到size有分歧的时候,考虑最差情况就是完全二叉树
完全二叉树的情况下复杂度是O(nlogn)的,所以这个算法是work的

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=2e5; 4 vector<int>g[maxn+5]; 5 int ans[maxn+5],fa[maxn+5]; 6 int n; 7 bool check(int x,int y) 8 { 9 queue<int> p,q; 10 p.push(x); 11 q.push(y); 12 while(true) 13 { 14 if(p.empty()) return true; 15 if(q.empty()) return false; 16 x=p.front(),p.pop(); 17 y=q.front(),q.pop(); 18 if(g[x].size()!=g[y].size()) return g[x].size()<g[y].size(); 19 for(int i=0;i<g[x].size();++i) p.push(g[x][i]); 20 for(int i=0;i<g[y].size();++i) q.push(g[y][i]); 21 } 22 return true; 23 } 24 void dfs(int k) 25 { 26 for(int i=0;i<g[k].size();++i) dfs(g[k][i]); 27 if(g[k].size()==2) 28 if(check(g[k][0],g[k][1])) swap(g[k][0],g[k][1]); 29 } 30 void paint() 31 { 32 queue<int> q; 33 vector<int> a; 34 q.push(1); 35 int id=0; 36 while(!q.empty()) 37 { 38 int u=q.front(); 39 //printf("ce : %d\n",u); 40 q.pop(); 41 ++id; 42 ans[u]=id; 43 if(u!=1) a.push_back(ans[fa[u]]-1); 44 for(int i=0;i<g[u].size();++i) q.push(g[u][i]); 45 } 46 for(int i=0;i<a.size()-1;++i) printf("%d ",a[i]);printf("%d",a[a.size()-1]); 47 printf("\n"); 48 } 49 int main() 50 { 51 freopen("ce.in","r",stdin); 52 int T; 53 scanf("%d",&T); 54 while(T--) 55 { 56 scanf("%d",&n); 57 for(int i=0;i<=n;++i) g[i].clear(); 58 for(int i=2;i<=n;++i) 59 { 60 int x; 61 scanf("%d",&x); 62 ++x; 63 g[x].push_back(i); 64 fa[i]=x; 65 } 66 dfs(1); 67 //printf("ok\n"); 68 paint(); 69 } 70 return 0; 71 }
F
待填坑
G(模拟)
题意:
在二维平面上有n个点,你需要开车走折线依次通过这些点,你最初在1号点,问你最少需要转弯多少次才能依次经过这n个点?
n<=1000
分析:
样例比较良心
我们把所有点按照顺序连一下,发现只有出现下面这个情形的时候我们才会做更改
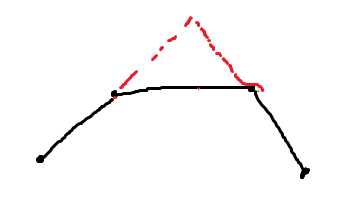
那么我们只需要从前到后去看有多少个这个结构就行了

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e3; 4 struct Point 5 { 6 int x,y; 7 Point() 8 { 9 10 } 11 Point(int _x,int _y) 12 { 13 x=_x,y=_y; 14 } 15 Point operator - (const Point &a) const 16 { 17 return Point(x-a.x,y-a.y); 18 } 19 }p[maxn+5]; 20 bool flag[maxn+5]; 21 int n,top,ans; 22 int cross(Point a,Point b) 23 { 24 return a.x*b.y-a.y*b.x; 25 } 26 bool pall(Point a,Point b) 27 { 28 if(cross(a,b)!=0) return false; 29 return a.x*b.x+a.y*b.y>0; 30 } 31 int main() 32 { 33 freopen("ce.in","r",stdin); 34 //freopen("ce.out","w",stdout); 35 int T; 36 scanf("%d",&T); 37 while(T--) 38 { 39 scanf("%d",&n); 40 for(int i=1;i<=n;++i) scanf("%d%d",&p[i].x,&p[i].y); 41 for(int i=0;i<=n;++i) flag[i]=0; 42 if(n<=2) 43 { 44 printf("0\n"); 45 continue; 46 } 47 ans=0; 48 for(int i=3;i<=n;++i) 49 { 50 if(!pall(p[i]-p[i-1],p[i-1]-p[i-2])) ++ans; 51 //printf("%d\n",ans); 52 if(i!=3) 53 if(!flag[i-1]&&!flag[i-2]&&1LL*cross(p[i-1]-p[i-2],p[i]-p[i-1])*cross(p[i-2]-p[i-3],p[i-1]-p[i-2])>0&&cross(p[i]-p[i-1],p[i-2]-p[i-3])!=0) 54 { 55 if(1LL*cross(p[i-2]-p[i-3],p[i]-p[i-1])*cross(p[i-2]-p[i-3],p[i-1]-p[i-2])>0) 56 { 57 58 59 --ans; 60 flag[i-1]=1; 61 } 62 } 63 64 } 65 printf("%d\n",ans); 66 } 67 return 0; 68 }
H(状压dp+递归)
题意:
有m道题目,有n个人,用0/1表示每个人是否会做每道题。现在你需要从m道题中挑出8道题组成一场考试,n个人进行这场考试。若一个人至少做出了5题,那么他就及格了。现在问你有多少种组题方案使得最后及格的人数在[l,r]之间并且是3的倍数。
3<=n<=500000 8<=m<=20 3<=l<=r<=n
分析:
枚举每一种组题的方案,计算该组题情况下最后及格的人数
容易想到需要将每个人的解题状态找一个共同的性质把其压缩起来,才能够减少最后的状态数,不然对于每种组题方案都要O(n)遍历
dp[i][s1][j][s2]表示对于前i道题,题目的选择情况是s1,答对了j个题,且这些人后面的答题情况是s2的总人数
很明显s1只有前i位有用,s2只有i后面的有用,于是我们把s1和s2状态合并到一起
那么显然就能状压dp了
分析一下复杂度,是$20*2^{20}*5$的
这是有点超时的,优化常数也不能在1s内通过
研究下原因是题目限定了“选8道题”,所以由很多选题状态都是无用的
于是我们用dfs去代替for循环枚举,就能800ms过了
I(计数+BIT)
题意:

n<=1e6
分析:
仔细分析会发现这个上升序列和下降序列一定会交于唯一位置(枚举这个位置给上升还是下降,会产生两种方案)
那么我们只需要枚举这个交点i,然后统计这个交点是否能对答案产生贡献
能产生贡献那就是:i前面比a[i]小的数字呈上升趋势,比a[i]大的数字呈下降趋势;i后面比a[i]小的数字呈下降趋势,比a[i]大的数字呈上升趋势
那么如何判断呢?以判断i前面比a[i]小的数字是否呈上升趋势为例
我们只需要统计出两个东西,一个东西是从左往右以a[i]为栈顶的单调栈的元素个数,另一个东西是1~i中<=a[i]的数字个数
第二个东西我们只需要用BIT来计算就行了
J
待填坑

