博弈论（巴什博奕，威佐夫博弈，尼姆博弈，斐波那契博弈）

一、巴什博弈（Bash Game）

有n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个，最后取光者得胜。

显然，如果n=m+1，那么由于一次最多只能取m个，所以，无论先取者拿走多少个，后取者都能够一次拿走剩余的物品，后取者取胜。因此我们发现了如何取胜的法则：

如果n=（m+1）*k+c，（c为任意自然数，c≤m)，那么先取者要拿走c个物品，如果后取者拿走x个（x≤m)，那么先取者再拿走m+1-x个，结果剩下（m+1）（k-1）个，以后保持这样的取法，那么先取者肯定获胜。总之，要保持给对手留下（m+1）的倍数，就能最后获胜。

所以我们可以知道，如果c=0，即满足n%（m+1）=0，则后手必胜，否则先手必胜。

#include <iostream>
using namespace std;
int main()
{
    int n,m;
    while(cin>>n>>m)
    {
        if(n%(m+1)==0)
        cout<<"later win"<<endl;
        else cout<<"earlier win"<<endl;    
    }
    return 0;
}

假如我们规定最后取光者输，那么结果又会如何呢？

如若满足（n-1）%（m+1）=0，则后手必胜，否则先手必胜。

所以可见其结果并不是简单的相反而已。

二、威佐夫博弈（Wythoff Game）

有两堆若干数量的物品，两人轮流从其中一堆取至少一件物品，至多不限，或从两堆中同时取相同件物品，规定最后取完者胜利。

直接说结论了，若两堆物品的初始值分别为n和m，且n>m。

若满足（int）[（（sqrt（5）+1）/2）*（n-m）]=m，则后手必胜，否则先手必胜。

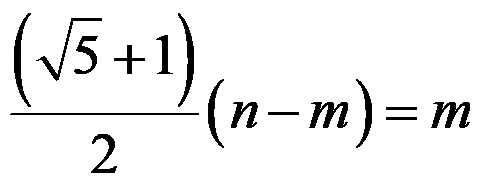【tip：左式需先取整！！】

#include <cstdio>  
#include <cmath>  
#include <iostream>  
using namespace std;  
int main()  
{  
    int n,m;
    while(cin>>n>>m)  
    {  
        if(m>n)
        swap(n,m);  
        if(floor((n-m)*(1+sqrt(5.0))/2.0)==m) 
        cout<<"later win"<<endl;  
        else cout<<"earlier win"<<endl;  
    }  
    return 0; 
}