Aiiage Camp Day1 A Littrain is a loser, in 2018

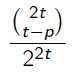 1 #include <bits/stdc++.h>
 2 #define MOD 1000000007
 3 using namespace std;
 4 
 5 typedef long long LL;
 6 
 7 LL jc[200010];
 8 
 9 LL inv(LL t, LL p)
10 {
11     return t == 1 ? 1 : (p - p / t) * inv(p % t, p) % p;
12 }
13 
14 void ycl()
15 {
16     jc[0] = 1;
17     for (int i = 1; i <= 200005; ++i)
18         jc[i] = (jc[i - 1] * i) % MOD;
19 }
20 
21 LL C(LL n, LL m)
22 {
23     return (jc[n] * inv((jc[n - m] * jc[m]) % MOD, MOD)) % MOD;
24 }
25 
26 LL qpow(LL a, LL b)
27 {
28     LL c = 1;
29     while (b)
30     {
31         if (b & 1)
32             c = (c * a) % MOD;
33         a = (a * a) % MOD;
34         b >>= 1;
35     }
36     return c;
37 } 
38 
39 int main()
40 {
41     ycl();
42     int T;
43     scanf("%d", &T);
44     while (T--)
45     {
46         int t, p;
47         scanf("%d%d", &t, &p);
48         p = abs(p);
49         if (p > t)
50         {
51             puts("0");
52             continue;
53         }
54         printf("%d\n", (C(2 * t, t - p) * qpow(MOD + 1 >> 1, 2 * t)) % MOD);
55     }
56     
57     return 0;
58 }