| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 17245 | Accepted: 8461 |
Description
a1x13+ a2x23+ a3x33+ a4x43+ a5x53=0
The coefficients are given integers from the interval [-50,50].
It is consider a solution a system (x1, x2, x3, x4, x5) that verifies the equation, xi∈[-50,50], xi != 0, any i∈{1,2,3,4,5}.
Determine how many solutions satisfy the given equation.
Input
Output
Sample Input
37 29 41 43 47
Sample Output
654
Source
题意:
给出一个5元3次方程,输入其5个系数,求它的解的个数
其中系数 ai∈[-50,50] 自变量xi∈[-50,0)∪(0,50]
注意:
若x1 =a, x2=b ,x3=c ,x4=d,x5=e时,与 x1=b, x2=a ,x3=c ,x4 =d, x5=e 代入方程后都得到值0,那么他们视为不同的解。
解题思路:
要对方程做一个变形
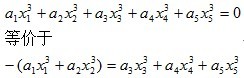
即先枚举x1和x2的组合,把所有出现过的 左值 记录打表,然后再枚举x3 x4 x5的组合得到的 右值,如果某个右值等于已经出现的左值,那么我们就得到了一个解
我们先定义一个映射数组Hash[],初始化为0
对于方程左边,sum1 = - (a1*x1*x1*x1 + a2*x2*x2*x2),遍历所有x1,x2的取值,并计数Hash[sum1]++
这里需要注意,sum1的取值范围为 -1250W ~1250W,所以我们进行计数的时候,将sum1+1250W,映射到0~2500W,避免数组越界,同时Hash的长度设置为2500W,进行计数时则为Hash[sum1 + 12500000]
同样的对于方程右边,sum2 = (a3*x3*x3*x3+a4*x4*x4*x4+a5*x5*x5*x5),便利所有的x3,x4,x5的取值,同样需要将sum2的取值做与sum1同样的映射,即sum2+12500000,注意sum2的取值范围大于sum1的取值范围,所以对于sum2+12500000 > 25000000 和 sum2+12500000<0 的值要进行舍弃,否则会发生数组越界。
如果 0 < sum2+12500000 < 25000000 且 Hash[sum2+12500000] != 0,说明这个右值等于已经出现的左值,那么我们得到了一个解
1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 short Hash[25000001]; 5 int main() 6 { 7 int a1,a2,a3,a4,a5; 8 while(cin>>a1>>a2>>a3>>a4>>a5) 9 { 10 memset(Hash,0,sizeof(Hash)); 11 for(int x1=-50;x1<=50;x1++) 12 { 13 if(x1 == 0) continue; 14 for(int x2=-50;x2<=50;x2++) 15 { 16 if(x2 == 0) continue; 17 int sum1 = -(a1*x1*x1*x1+a2*x2*x2*x2); 18 Hash[sum1+12500000]++;//将sum1-12500000~12500000映射到0~25000000 19 } 20 } 21 int solution = 0; 22 for(int x3=-50;x3<=50;x3++) 23 { 24 if(x3 == 0) continue; 25 for(int x4=-50;x4<=50;x4++) 26 { 27 if(x4 == 0) continue; 28 for(int x5=-50;x5<=50;x5++) 29 { 30 if(x5 == 0) continue; 31 int sum2 = (a3*x3*x3*x3+a4*x4*x4*x4+a5*x5*x5*x5); 32 if(sum2+12500000 > 25000000 || sum2+12500000<0) continue; 33 if(Hash[sum2+12500000]) 34 solution+=Hash[sum2+12500000]; 35 } 36 } 37 } 38 cout<<solution<<endl; 39 } 40 return 0; 41 }

