Description
想必大家都看过成龙大哥的《 \(80\) 天环游世界》,里面的紧张刺激的打斗场面一定给你留下了深刻的印象。现在就有这么
一个 \(80\) 人的团伙,也想来一次环游世界。
他们打算兵分多路,游遍每一个国家。
因为他们主要分布在东方,所以他们只朝西方进军。设从东方到西方的每一个国家的编号依次为 \(1\cdots N\) 。假若第i个人的游历路线为 \(P_1,P_2\cdots P_k(0\le k\le N)\),则 \(P_1<P_2<\cdots <P_k\) 。
众所周知,中国相当美丽,这样在环游世界时就有很多人经过中国。我们用一个正整数 \(V_i\) 来描述一个国家的吸引程度,Vi值越大表示该国家越有吸引力,同时也表示有且仅有 \(V_i\) 个人会经过那一个国家。
为了节省时间,他们打算通过坐飞机来完成环游世界的任务。同时为了省钱,他们希望总的机票费最小。
明天就要出发了,可是有些人临阵脱逃,最终只剩下了 \(M\) 个人去环游世界。他们想知道最少的总费用,你能告诉他们吗?
Input
第一行两个正整数 \(N,M\) 。
第二行有 \(N\) 个不大于 \(M\) 正整数,分别表示 \(V_1,V_2\cdots V_N\)。
接下来有 \(N-1\) 行。第 \(i\) 行有 \(N -i\) 个整数,该行的第 \(j\) 个数表示从第 \(i\) 个国家到第 \(i+j\) 个国家的机票费(如果该值等于 \(-1\) 则表示这两个国家间没有通航)。
Output
在第一行输出最少的总费用。
Sample Input
6 3
2 1 3 1 2 1
2 6 8 5 0
8 2 4 1
6 1 0
4 -1
4Sample Output
27HINT
\(1\le N \le 100,1\le M \le 79\)
Solution

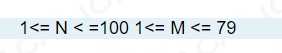
这大概就是题面钦定数据范围吧...
这是一道上下界费用流。
将国家 \(x\) 拆成入点 \(x_1\) ,出点 \(x_2\) ,同时建源点 \(S\) ,汇点 \(T\) ,第二源点 \(SS\) 。
首先 \[<S, SS>:capacity=m,cost=0\]
对于国家 \(x\) \[<SS,x_1>:capacity=INF,cost = 0\] \[<x_2,T>:capacity=INF,cost=0\] \[<x_1,x_2>:capacity=[V, V],cost=0\]
如果 \(x\) 到 \(y\) 有航线,则 \[<x_2,y_1>:capacity=INF,cost=W\]
然后跑一个上下界费用流即可。具体做法是先把每条边的 \(lw\) 乘上 \(cost\) 加到答案里(当然本题不需要),再跑一个普通的费用流。
#include<bits/stdc++.h>
using namespace std;
#define N 1001
#define INF 2000000000
#define rep(i, a, b) for (int i = a; i <= b; i++)
#define ll long long
inline int read() {
int x = 0, flag = 1; char ch = getchar(); while (!isdigit(ch)) { if (!(ch ^ '-')) flag = -1; ch = getchar(); }
while (isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar(); return x * flag;
}
int n, m, SS, SSS, TT;
int du[N];
int S, T, flow, cost;
struct edge { int u, v, c, w, next; }e[20001];
int head[N], tot = 1;
int dis[N], pre[N];
queue<int> q;
bool inq[N];
inline void insert(int u, int v, int c, int w) { e[++tot].u = u, e[tot].v = v, e[tot].c = c, e[tot].w = w, e[tot].next = head[u], head[u] = tot; }
inline void add(int u, int v, int c, int w) { insert(u, v, c, w), insert(v, u, 0, -w); }
inline bool spfa() {
rep(i, S, T) dis[i] = INF; dis[S] = 0; q.push(S);
while (!q.empty()) {
int u = q.front(); q.pop(); inq[u] = 0;
for (int i = head[u], v, w; i; i = e[i].next) if (e[i].c > 0 && dis[v = e[i].v] > dis[u] + (w = e[i].w)) {
dis[v] = dis[u] + w, pre[v] = i;
if (!inq[v]) q.push(v); inq[v] = 1;
}
}
return dis[T] != INF;
}
inline void mcf() {
int d = INF;
for (int i = T; (i ^ S); i = e[pre[i]].u) d = min(d, e[pre[i]].c);
flow += d;
for (int i = T; (i ^ S); i = e[pre[i]].u) e[pre[i]].c -= d, e[pre[i] ^ 1].c += d, cost += d * e[pre[i]].w;
}
int main() {
cin >> n >> m; SSS = 2 * n + 1, SS = SSS + 1, TT = SS + 1, T = TT + 1;
rep(i, 1, n) {
add(SSS, i, INF, 0), add(i + n, TT, INF, 0);
int V = read(); add(i, i + n, 0, 0);
du[i] -= V, du[i + n] += V;
}
add(SS, SSS, m, 0);
rep(i, 1, n) rep(j, i + 1, n) { int V = read(); if(V != -1) add(i + n, j, INF, V); }
add(TT, SS, INF, 0);
rep(i, 1, TT) if (du[i] > 0) add(S, i, du[i], 0); else add(i, T, -du[i], 0);
while (spfa()) mcf(); cout << cost;
return 0;
}