2018清华冬令营
又一次由于接连而至的玄学现象跪惨,错失良机,就不再公开提我这次惨痛的经历了,写点干货……
day1
A 零食 (1s, 1G)
试题简述
\(n\) 种物品1,\(m\) 种物品2,要求安排一个两种物品的排列,当且仅当某个物品的有前一个物品前一个物品种类和它一样时才能让总和增加这个物品的权值。
现给出所有物品的权值,求最大总和。
输入
第一行一个整数 \(T\),表示数据组数。
第二行一个正整数 \(n\),表示物品1的个数。
第三行 \(n\) 个整数,\(A_1, A_2, \cdots , A_n\),分别表示所有物品1的权值。
第四行一个正整数 \(m\),表示物品2的个数。
第五行 \(m\) 个整数,\(B_1, B_2, \cdots , B_n\),分别表示所有物品2的权值。
输出
一个整数,表示最大总和。
输入示例
2
5
2 3 3 -3 -3
5
6 6 6 -6 -6
2
1 -1
3
1 -1 1输出示例
26
3数据规模及约定
\(1 \le n, m \le 10^6, |A_i|, |B_i| \le 10^9\)
题解
容易想到两种物品“被消掉”(权值没有被计入总和)的个数至多相差 \(1\),于是我们枚举物品1被消掉的个数,物品2被消掉的个数可以随之确定,而我们肯定是要贪心地消两种物品中权值小的物品,所以最终给 \(A\) 和 \(B\) 排个序扫一遍就好了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 1000010
#define LL long long
#define ool (1ll << 60)
int n, m, A[maxn], B[maxn];
LL sA[maxn], sB[maxn];
LL sufA(int x) { return x <= n ? sA[x] : 0; }
LL sufB(int x) { return x <= m ? sB[x] : 0; }
void work() {
n = read();
rep(i, 1, n) A[i] = read();
m = read();
rep(i, 1, m) B[i] = read();
sort(A + 1, A + n + 1);
sort(B + 1, B + m + 1);
sA[n+1] = 0; dwn(i, n, 1) sA[i] = sA[i+1] + A[i];
sB[m+1] = 0; dwn(i, m, 1) sB[i] = sB[i+1] + B[i];
LL ans = -ool;
rep(i, 1, min(n, m)) {
if(i <= n && i <= m) ans = max(ans, sufA(i + 1) + sufB(i + 1));
if(i <= n && i + 1 <= m) ans = max(ans, sufA(i + 1) + sufB(i + 2));
if(i + 1 <= n && i <= m) ans = max(ans, sufA(i + 2) + sufB(i + 1));
}
printf("%lld\n", ans);
return ;
}
int main() {
int T = read();
while(T--) work();
return 0;
}B 城市规划 (1.5s, 2G)
试题简述
\(n\) 个节点的树,节点 \(i\) 有颜色 \(a_i\),求包含不超过两种颜色的连通块个数模 \(998244353\) 后的值。
输入
第一行一个正整数 \(n\)。
第二行 \(n\) 个正整数 \(a_1, a_2, \cdots , a_n\)。
接下来 \(n-1\) 行,每行两个正整数 \(u_i, v_i\),描述一条树边。
输出
取模后的答案。
输入示例
6
1 1 2 3 4 5
1 2
1 3
1 4
2 5
2 6输出示例
15数据规模及约定
\(1 \le a_i, u_i, v_i \le n \le 10^5\)
题解
考虑一个暴力的 dp,设 \(f(i, c)\) 表示包含节点 \(i\) 和 \(i\) 子树中的节点,其中一种颜色为 \(a_i\),另一种颜色为 \(c\) 的连通块个数。特别地,当 \(c=0\) 时,该连通块只包含颜色 \(a_i\)(可以知道,只包含节点 \(i\) 的连通块也会被统计到 \(f(i, 0)\) 中)。
分两种转移(令 \(A_i\) 表示节点 \(i\) 的 dp 值的颜色集合):
- 对于一个 \(i\) 的儿子 \(son\),若 \(a_{son} \ne a_i\),那么 \(f(i, a_{son}) \leftarrow f(son, a_i) + f(son, 0) + 1\),其中 \(a \leftarrow b\) 表示将 \(b\) 累乘到 \(a\) 中。为什么要加 \(1\) 呢,因为不选择这个子树也是一种方案。
- 若 \(a_{son} = a_i\),\(\forall c \in A_i \bigcup A_{son}, f(i, c) \leftarrow f(son, c) + f(son, 0) + 1\)。
- 特殊地计算一下 \(f(i, 0) = \prod_{a_{son} \ne a_i} (f(son, 0) + 1)\),我就不把它算作“一种转移”了。
但是这样转移完还不算结束,容易发现我们对于所有出现过的颜色 \(c\),都多统计了 \(f(i, 0)\) 的方案,也就是说,所有的 \(f(i, c)\) 要减去 \(f(i, 0)\) 才能得到真正的 dp 值。
不难发现一个节点 \(i\) 的 dp 值只需要存储它子树中出现过的颜色,而上面的第一种转移相当于单点修改,第二种转移相当于同类合并。那么我们写一个线段树合并就能均摊 \(O(n \log n)\) 支持所有的转移操作了。
为什么线段树合并格外好写呢,因为它天然支持区间加和区间乘。
为了方便,我们可以对于所有出现过的 \(f(i, c)\) 最后不减去 \(f(i, 0)\),因为上面所有的转移式子中其实都是形如 \(f(i, c) + f(i, 0) + 1\),如果我们不减去,式子就简化成了 \(f(i, c) + 1\),下面的代码也是这样实现的。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cassert>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 100010
#define maxm 200010
#define maxnode 4000010
#define MOD 998244353
#define LL long long
int n, m, head[maxn], nxt[maxm], to[maxm], col[maxn];
void AddEdge(int a, int b) {
to[++m] = b; nxt[m] = head[a]; head[a] = m;
swap(a, b);
to[++m] = b; nxt[m] = head[a]; head[a] = m;
return ;
}
int ToT, rt[maxnode], lc[maxnode], rc[maxnode], mulv[maxnode], addv[maxnode], sumv[maxnode], siz[maxnode];
int f0;
void multi(int& a, int b) {
a = (LL)a * b % MOD;
return ;
}
void incr(int& a, int b) {
a += b; if(a >= MOD) a -= MOD;
return ;
}
void pushdown(int o, int l, int r) {
if((!addv[o] && mulv[o] == 1) || l == r){ mulv[o] = 1; addv[o] = 0; return ; }
assert(l > 0);
if(lc[o])
multi(mulv[lc[o]], mulv[o]), multi(addv[lc[o]], mulv[o]), multi(sumv[lc[o]], mulv[o]), incr(addv[lc[o]], addv[o]), incr(sumv[lc[o]], (LL)addv[o] * siz[lc[o]] % MOD);
if(rc[o])
multi(mulv[rc[o]], mulv[o]), multi(addv[rc[o]], mulv[o]), multi(sumv[rc[o]], mulv[o]), incr(addv[rc[o]], addv[o]), incr(sumv[rc[o]], (LL)addv[o] * siz[rc[o]] % MOD);
mulv[o] = 1; addv[o] = 0;
return ;
}
void Mul(int& o, int l, int r, int p, int v) {
bool isnew = 0;
if(!o) mulv[o = ++ToT] = 1, isnew = 1;
else pushdown(o, l, r);
if(l == r) {
siz[o] = 1;
if(isnew) sumv[o] = v;
else multi(sumv[o], v);
// printf("sumv[%d] = %d\n", o, sumv[o]);
return ;
}
int mid = l + r >> 1;
if(p <= mid) Mul(lc[o], l, mid, p, v);
else Mul(rc[o], mid + 1, r, p, v);
sumv[o] = sumv[lc[o]] + sumv[rc[o]]; if(sumv[o] >= MOD) sumv[o] -= MOD;
siz[o] = siz[lc[o]] + siz[rc[o]];
return ;
}
int query(int o, int l, int r, int p) {
if(!o) return f0;
pushdown(o, l, r);
if(l == r) return sumv[o];
int mid = l + r >> 1;
if(p <= mid) return query(lc[o], l, mid, p);
return query(rc[o], mid + 1, r, p);
}
void update_add(int& o, int l, int r, int v) {
assert(l > 0);
pushdown(o, l, r);
incr(sumv[o], (LL)v * siz[o] % MOD);
incr(addv[o], v);
return ;
}
void update_mul(int& o, int l, int r, int v) {
assert(l > 0);
pushdown(o, l, r);
multi(sumv[o], v);
multi(mulv[o], v);
return ;
}
int Merge(int x, int y, int l, int r) {
if(!x && !y) return 0;
if(!x){ update_add(y, l, r, 1); return y; }
if(!y){ update_mul(x, l, r, f0 + 1); return x; }
pushdown(x, l, r); pushdown(y, l, r);
if(l == r){ multi(sumv[x], (sumv[y] + 1)); return x; }
int mid = l + r >> 1;
lc[x] = Merge(lc[x], lc[y], l, mid); rc[x] = Merge(rc[x], rc[y], mid + 1, r);
sumv[x] = sumv[lc[x]] + sumv[rc[x]]; if(sumv[x] >= MOD) sumv[x] -= MOD;
siz[x] = siz[lc[x]] + siz[rc[x]];
return x;
}
int ans;
void dp(int u, int fa) {
bool has = 0;
for(int e = head[u]; e; e = nxt[e]) if(to[e] != fa) dp(to[e], u), has = 1;
Mul(rt[u], 0, n, 0, 1);
if(has) {
for(int e = head[u]; e; e = nxt[e]) if(to[e] != fa) {
f0 = query(rt[to[e]], 0, n, 0);
if(col[to[e]] != col[u]) Mul(rt[u], 0, n, col[to[e]], (query(rt[to[e]], 0, n, col[u]) + 1) % MOD);
else rt[u] = Merge(rt[u], rt[to[e]], 0, n);
}
int tmp = sumv[rt[u]];
incr(tmp, MOD - (LL)(siz[rt[u]] - 1) * query(rt[u], 0, n, 0) % MOD);
incr(ans, tmp);
}
else incr(ans, 1);
/*f0 = query(rt[u], 0, n, 0);
rep(i, 0, n) printf("f[%d][%d] = %d\n", u, i, query(rt[u], 0, n, i) - (i ? f0 : 0)); // */
return ;
}
int main() {
n = read();
rep(i, 1, n) col[i] = read();
rep(i, 1, n - 1) {
int a = read(), b = read();
AddEdge(a, b);
}
dp(1, 0);
printf("%d\n", ans);
return 0;
}C 字胡串 (3s, 512MB)
试题简述
给出长度为 \(n\) 的串 \(A\),和 \(q\) 个询问。每个询问是一个串 \(B_i\),要求回答一个最小的 \(j\),使得 \(A[1..j] + B_i + A[j+1..n]\) 字典序最小。
输入
第一行一个正整数 \(n\)。
第二行一个数字串 \(A\)。
第三行一个正整数 \(q\)。
接下来 \(q\) 行,每行一个数字串 \(B_i\)。
输出
\(q\) 行,分别为每组询问的答案
输入示例1
6
000001
2
00
01输出示例1
0
5输入示例2
10
7676767982
1
7676输出示例2
0数据规模及约定
\(1 \le n, q, \sum |B_i| \le 10^6\),\(1 \le \max\{ |B_i| \} \le n\),输入的字符串均为字符集为全体数字的串。
题解
看到这题要理清思路,要求最小化字典序,那么自然是从前往后贪心地考虑每一位,并让每一位尽量低,于是现在需要考虑清楚,插入后的串的一个前缀到底是由什么构成的?不难发现情况有三种:
- \(A\) 的前缀,形式化地:\(A[1..i]\);
- \(A\) 的前缀 + \(B\) 的前缀,形式化地:\(A[1..i] + B[1..j]\);
- \(A\) 的前缀 + \(B\) + \(A\) 后面的一段,形式化地:\(A[1..i] + B + A[i+1..k]\)。
情况1不需要考虑,因为这时候还未引入串 \(B\)。
可以发现情况3也可以忽略,因为我们会在情况2中先找到“冲突”,而这时已经可以把 \(B\) 插入的位置确定下来了,没必要再去看情况3。
解释一下什么叫“冲突”,我们一定会找到一个 \((i, j)\) 满足 \(A[1..i] + B[1..j] < A[1..i+j]\)(假设串 \(A\) 后面追加一个字符 \(10\),它比任何数字字符都要大,这样就能够保证一定能找到这样一个位置)。不难发现我们希望 \(i+j\) 最小,因为字符变小的位置越靠前越好。
那么现在目标就是找到这个最小的 \(i+j\)。我们可以先枚举 \(j\),由于在 \(i\) 确定的情况下 \(j\) 要最小,所以会有 \(B[j] < A[i+j]\),那么我们可以构造一下 \(A\) 的后缀自动机,并查找 \(B[1..j-1] + x\) 的最靠前的匹配位置(\(x\) 从 \(B[j] + 1\) 到 \(10\) 枚举),这个最靠前的匹配位置就是 \(i\)。这样所有的取个最小值就可以求出最小的 \(i+j\) 了。
但是仅仅找到最小的 \(i+j\) 并不能得到最小字典序的串,假设对于 \(j_1\) 和 \(j_2\) 都有 \(A[1..i_1] + B[1..j_1] < A[1..i_1+j_1]\),\(A[1..i_2] + B[1..j_2] < A[1..i_2+j_2]\),那么 \(A[1..i_1] + B + A[i_1+1..n]\) 和 \(A[1..i_2] + B + A[i_2+1..n]\) 哪个更小呢?注意到这里有 \(i_1+j_1 = i_2+j_2\),那么 \(A[1..i_1] + B[1..j_1-1] = A[1..i_2] + B[1..j_2-1]\),于是我们可以直观地看下图:
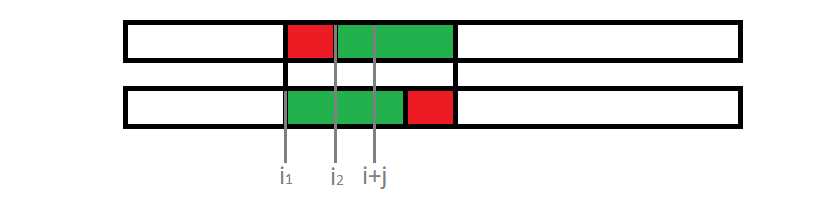
绿色部分表示串 \(B\),容易发现,这时只用比较 \(B\) 的后缀 \(B[j_1..l]\) 和 \(B[j_2..l]\)(\(l = |B|\))谁更靠前就好了(所以要再打个后缀数组)。细心的读者一定发现,这样比较之后还有一个隐患:如果 \(B[j_2..l]\) 恰好是 \(B[j_1..l]\) 的前缀(不失一般性,这里假设 \(j_2 > j_1\)),怎么办呢?可以证明,这样的话,两种方案得到的串是一样的。如图:
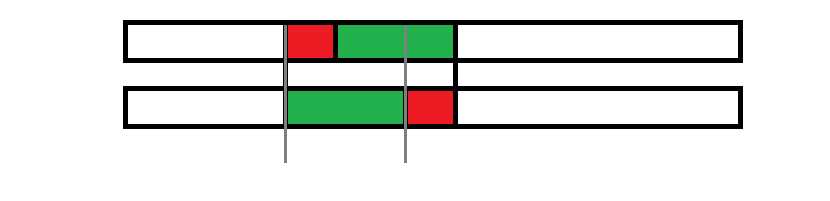
其中,两个灰色刻度之间的部分是相同的,那么可以发现红色部分是 \(B\) 的一个 border(若 \(|B|\) 小于红色部分的长度则 \(B\) 是红色部分的一个 border,不过不影响后面的结论),令红色部分长度为 \(l‘\),可以证明 \(B\) 是以 \(gcd(l, l‘)\) 为周期的一个周期串。那么图中 \(红串+绿串\) 和颠倒过来的 \(绿串+红串\) 就是完全一样的啦!
至此,我们还没有做完。因为我们刚刚得到一个能使得插入之后字典序最小的插入位置,这个插入位置可能有很多,我们要求出最小的那个。不难发现,所有可能的插入位置就是串 \(B\) 往前跳,所以我们用 KMP 找到 \(B\) 的最小周期,然后倍增 + 哈希往前跳就好了。(哈希是因为我们需要判断往前跳那么多步之后和跳之前的串完全相同)
纵观本题,竟然有四个字符串工具:SAM + SA + KMP + hash。实现的话,细节是相当多的。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = getchar(); }
return x * f;
}
#define maxn 4000010
#define maxlog 25
#define maxnode 8000010
#define maxa 11
#define oo 2147483647
int n, q;
char str[maxn], tmp[maxn];
int ToT, to[maxnode][maxa], par[maxnode], lst, mx[maxnode], mnp[maxnode];
void extend(int i) {
int c = str[i] - ‘0‘, now = ++ToT, v = lst; lst = now;
mx[now] = i; mnp[now] = i;
while(v && !to[v][c]) to[v][c] = now, v = par[v];
if(!v) par[now] = 1;
else {
int u = to[v][c];
if(mx[u] == mx[v] + 1) par[now] = u;
else {
int q = ++ToT; mx[q] = mx[v] + 1; mnp[q] = oo;
par[q] = par[u];
par[u] = par[now] = q;
memcpy(to[q], to[u], sizeof(to[u]));
while(v && to[v][c] == u) to[v][c] = q, v = par[v];
}
}
return ;
}
bool cmp(int a, int b) { return mx[a] < mx[b]; }
int id[maxnode];
void build() {
rep(i, 1, ToT) id[i] = i;
sort(id + 1, id + ToT + 1, cmp);
dwn(i, ToT, 1) {
int u = id[i];
mnp[par[u]] = min(mnp[par[u]], mnp[u]);
}
return ;
}
#define rate 233
#define UL unsigned long long
UL rpow[maxn], hval[maxn], htmp[maxn], jump[maxlog];
void hash_init() {
rpow[0] = 1;
rep(i, 1, n + 1) rpow[i] = rpow[i-1] * rate;
rep(i, 1, n) hval[i] = hval[i-1] * rate + str[i];
return ;
}
UL get_hash(int l, int r) {
return hval[r] - hval[l-1] * rpow[r-l+1];
}
struct SA {
char S[maxn];
int N, height[maxn], rank[maxn], sa[maxn], Ws[maxn];
bool diff(int *a, int p1, int p2, int len) {
if(p1 + len > N && p2 + len > N) return a[p1] != a[p2];
if(p1 + len > N || p2 + len > N) return 1;
return a[p1] != a[p2] || a[p1+len] != a[p2+len];
}
void ssort(char *tS) {
rep(i, 1, max(N, 10)) Ws[i] = 0;
N = strlen(tS);
rep(i, 1, N) S[i] = tS[i-1];
int *x = height, *y = rank, m = 0;
rep(i, 1, N) Ws[x[i] = S[i]-‘0‘+1]++, m = max(m, x[i]);
rep(i, 1, m) Ws[i] += Ws[i-1];
dwn(i, N, 1) sa[Ws[x[i]]--] = i;
for(int j = 1, pos; j < N; j <<= 1, m = pos) {
pos = 0;
rep(i, N - j + 1, N) y[++pos] = i;
rep(i, 1, N) if(sa[i] > j) y[++pos] = sa[i] - j;
rep(i, 1, m) Ws[i] = 0;
rep(i, 1, N) Ws[x[i]]++;
rep(i, 1, m) Ws[i] += Ws[i-1];
dwn(i, N, 1) sa[Ws[x[y[i]]]--] = y[i];
swap(x, y); x[sa[1]] = pos = 1;
rep(i, 2, N) x[sa[i]] = diff(y, sa[i], sa[i-1], j) ? ++pos : pos;
}
rep(i, 1, N) rank[sa[i]] = i;
return ;
}
} cmper;
int fa[maxn];
int main() {
n = read();
scanf("%s", str + 1);
ToT = lst = 1; mnp[1] = oo;
rep(i, 1, n) extend(i);
rep(i, n + 1, n << 1) str[i] = 10 + ‘0‘, extend(i);
n <<= 1;
build();
hash_init();
int q = read();
while(q--) {
scanf("%s", tmp + 1);
cmper.ssort(tmp + 1);
int now = 1, bestl = 0, bestp = -1, len = strlen(tmp + 1);
// rep(i, 1, len) printf("%d%c", cmper.rank[i], i < len ? ‘ ‘ : ‘\n‘);
rep(i, 1, len) {
rep(c, tmp[i] - ‘0‘ + 1, 10) if(to[now][c]) {
int u = to[now][c];
if(!bestl || bestp > mnp[u] || (bestp == mnp[u] && cmper.rank[i] < cmper.rank[bestl]))
bestp = mnp[u], bestl = i;
}
now = to[now][tmp[i]-‘0‘];
if(!now) break;
}
fa[1] = fa[2] = 1;
rep(i, 2, len) {
int j = fa[i];
while(j > 1 && tmp[j] != tmp[i]) j = fa[j];
fa[i+1] = tmp[j] == tmp[i] ? j + 1 : 1;
}
rep(i, 1, len) htmp[i] = htmp[i-1] * rate + tmp[i];
// printf("bestp: %d %d\n", bestp, bestl);
bestp -= bestl;
int u = fa[len+1], ans = bestp;
while(1) {
int tlen = len + 1 - u;
if(tlen && len % tlen == 0) {
// printf("try tlen: %d\n", tlen);
jump[0] = htmp[tlen];
for(int i = 1; (1 << i) * tlen <= n; i++) jump[i] = jump[i-1] * rpow[(1<<i>>1)*tlen] + jump[i-1];
// for(int i = 0; (1 << i) * tlen <= n; i++) printf("jump[%d]: %llu\n", i, jump[i]);
int np = bestp;
dwn(i, maxlog - 1, 0)
if(np - (1ll << i) * tlen >= 0 && get_hash(np - (1 << i) * tlen + 1, np) == jump[i])
np -= (1ll << i) * tlen;
ans = min(ans, np);
break;
}
if(u == 1) break;
u = fa[u];
}
printf("%d\n", ans);
}
return 0;
}day2
A 明天的太阳会照常升起 (7s, 512MB)
试题简述
\(n\) 个城市从北往南依次编号为 \(1 \sim n\),城市 \(i\) 和城市 \(i+1\) 之间有一条长度为 \(l_i\) 的道路 \((1 \le i < n)\),城市 \(i\) 加 \(1\) 单位油的价钱为 \(p_i\),\(1\) 单位油可以走 \(1\) 单位距离。
现有 \(m\) 组询问,每次询问形如 \((s_i, t_i, v_i)\),表示从城市 \(s_i\) 开车到 \(t_i\),初始时油量为 \(v_i\) 所需的最小花费。
注意:每组询问中车都有恒定的油量上界 \(V\)。
输入
第一行三个正整数 \(n, m, V\)。
第二行 \(n\) 个正整数 \(p_1, p_2, \cdots , p_n\)。
第三行 \(n-1\) 个正整数 \(l_1, l_2, \cdots, l_{n-1}\)。
接下来 \(m\) 行,每行三个正整数 \(s_i, t_i, v_i\),表示一组询问。
输出
\(m\) 行,分别为每组询问的答案
输入示例
7 2 9
3 2 5 6 7 4 1
2 5 7 7 3 4
1 4 2
2 6 5输出示例
33
82数据规模及约定
\(1 \le m, p_i \le 10^6\),\(1 \le V \le 10^{18}\),\(1 \le l_i, v_i \le \min\{ 10^6, V \}\),\(1 \le s_i < t_i \le n \le 10^6\)。
题解
首先考虑暴力每次询问从 \(s\) 到 \(t\) 线性扫一遍,显然我们需要决策的就是在每个城市是否要加油,如果要,加多少。不难发现一个显然的贪心策略:到一个城市 \(i\) 后,如果对于 \(j > i\) 且 \(p_j < p_i\) 或 \(j = t\) 的最小的 \(j\) 有 \(\sum_{k=i}^{j-1} l_k \le V\),那么我们把油量加到 \(\sum_{k=i}^{j-1} l_k\),否则加满(即加到 \(V\))。
那么现在的任务无非是利用数据结构优化这个暴力的过程。
只考虑暴力中会加油的那些城市,我们发现遵循这样一个规则:若在城市 \(i\) 加油,那么下一个加油的城市可以唯一确定出来,分两种情况确定:
- 对于 \(j > i\) 且 \(p_j < p_i\) 的最小的 \(j\),有 \(\sum_{k=i}^{j-1} l_k \le V\),那么下一个加油的城市就是 \(j\);
- 否则下一个加油的城市是从 \(i\) 往后 \(V\) 的距离中 \(p_j\) 最小的城市 \(j\)。
容易发现每个城市只有一个“下一个加油的城市”,所以如果把这个关系图建出来,这就是一棵树。树上的操作就很好办了,从一个点跳到另一个点,自然想到倍增。
但是两个问题,一是如何解决初始油量,二是如何解决限定终点。
一下我们将节点分成两类,下一个价格更便宜的城市到这个城市的距离 \(\le V\) 的称作第一类,否则称作第二类。
问题一很好解决,我们先倍增往上跳,当遇到一个第二类或者初始油量不够往上跳的时候结束。以这时所在的节点 \(s‘\) 为新的起点,并设这时剩下的油量为 \(v‘\)。那么这时可以保证下一步跳所花费的价格可以直接减去 \(v‘ \cdot p_{s‘}\)。
对于问题二,我们可以倍增找到第一次遇到的可以“直接到达 \(t\) 的节点”。\(i\) 可以直接到达的含义是:若 \(i\) 是第一类城市,那么它到它父亲节点的距离大于等于它到 \(t\) 的距离;否则 \(V\) 大于等于它到 \(t\) 的距离。找到这样的节点后,一步跳到 \(t\) 即可。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
#define LL long long
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
LL read() {
LL x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 1000010
#define maxlog 20
int n, q, pri[maxn];
LL lim, D[maxn];
LL cdist(int a, int b) { b = min(b, n); return D[b-1] - D[a-1]; }
int nxt[maxn], fa[maxn][maxlog], mnp[maxlog][maxn], Log[maxn];
bool type[maxn];
LL cost[maxn][maxlog], rest[maxn][maxlog];
int qmin(int l, int r) {
int t = Log[r-l+1], a = mnp[t][l], b = mnp[t][r-(1<<t)+1];
return pri[a] < pri[b] ? a : b;
}
void init() {
pri[n+1] = 0;
dwn(i, n, 1) {
nxt[i] = i + 1;
while(pri[nxt[i]] > pri[i]) nxt[i] = nxt[nxt[i]];
}
Log[1] = 0;
rep(i, 2, n) Log[i] = Log[i>>1] + 1;
rep(i, 1, n) mnp[0][i] = i;
for(int j = 1; (1 << j) <= n; j++)
rep(i, 1, n - (1 << j) + 1) {
int a = mnp[j-1][i], b = mnp[j-1][i+(1<<j>>1)];
mnp[j][i] = pri[a] < pri[b] ? a : b;
}
rep(i, 1, n)
if(cdist(i, nxt[i]) <= lim) {
fa[i][0] = nxt[i];
cost[i][0] = cdist(i, nxt[i]) * pri[i];
rest[i][0] = 0;
type[i] = 0;
}
else {
int l = i + 1, r = n + 1;
while(r - l > 1) {
int mid = l + r >> 1;
if(cdist(i, mid) <= lim) l = mid; else r = mid;
}
l = qmin(i + 1, l);
fa[i][0] = l;
cost[i][0] = lim * pri[i];
rest[i][0] = lim - cdist(i, l);
type[i] = 1;
}
int now = n + 1;
dwn(i, n, 1) {
if(type[i]) now = i;
nxt[i] = now;
}
rep(j, 1, maxlog - 1) rep(i, 1, n) {
int m = fa[i][j-1];
fa[i][j] = fa[m][j-1];
cost[i][j] = cost[i][j-1] + cost[m][j-1] - rest[i][j-1] * pri[m];
rest[i][j] = rest[m][j-1];
}
return ;
}
int num[100], cntn;
void putint(LL x) {
cntn = 0;
while(x) num[++cntn] = x % 10, x /= 10;
dwn(i, cntn, 1) putchar(num[i] + ‘0‘); putchar(‘\n‘);
return ;
}
int main() {
n = read(); q = read(); lim = read();
rep(i, 1, n) pri[i] = read();
rep(i, 1, n - 1) D[i] = D[i-1] + read();
init();
while(q--) {
int s = read(), t = read(); LL v = read();
if(cdist(s, t) <= v){ puts("0"); continue; }
LL ans = 0;
dwn(i, maxlog - 1, 0) if(fa[s][i] && nxt[s] >= fa[s][i] && cdist(s, fa[s][i]) <= v)
v -= cdist(s, fa[s][i]), s = fa[s][i];
// printf("get1: %d\n", s);
dwn(i, maxlog - 1, 0) {
int tmp = fa[s][i];
if(!tmp || tmp > t) continue;
// if(i == 0) printf("tmp: %d %lld\n", tmp, cdist(tmp, t));
if((type[tmp] && lim >= cdist(tmp, t)) || (!type[tmp] && fa[tmp][0] && fa[tmp][0] >= t)) continue;
ans += cost[s][i] - v * pri[s];
v = rest[s][i]; s = fa[s][i];
}
if((type[s] && lim >= cdist(s, t)) || (!type[s] && fa[s][0] && fa[s][0] >= t));
else ans += cost[s][0] - v * pri[s], v = rest[s][0], s = fa[s][0];
// printf("get2: %d %lld %lld (%lld - %lld) * %d = %lld\n", s, v, ans, cdist(s, t), v, pri[s], (cdist(s, t) - v) * pri[s]);
ans += (cdist(s, t) - v) * pri[s];
putint(ans);
}
return 0;
}据说标程很短,不知怎么做到的。
B 小球序列 (5s, 512MB)
试题简述
有 \(k\) 种颜色的球,第 \(i\) 中颜色的球有 \(a_i\) 个,现在要你将它们排成一排,要求对于任意非空前缀、后缀都满足 \(k\) 中颜色的小球个数不同。
求排列方案数对 \(998244353\) 取模后的结果。
输入
第一行一个正整数 \(k\)。
第二行 \(k\) 个正整数 \(a_1, a_2, \cdots , a_k\)。
输出
取模后的答案。
输入示例
3
1 2 1输出示例
2数据规模及约定
\(1 \le k \le 100, 1 \le a_i \le 2 \times 10^5\)。
题解
这种题还是得从暴力 dp 入手。我们发现问题可以转化成 \(k\) 维空间中,不能经过两条直线上的点,每次只能沿某个维度的正方向走,问从 \((0, 0, \cdots , 0)\) 到 \((a_1, a_2, \cdots , a_k)\) 有多少条路径。
以下令 \(n = \min_{i \in [1, k]} a_i\)。
这个问题 \(O(n^2)\) 显然可以将所有被挖掉的点按照坐标排序,然后容斥 dp 一下做出来。
但由于这题的点的坐标非常特殊,我们可以利用这个条件进行优化。
先推一个小式子,从 \((x_1, x_2, \cdots , x_k)\) 到 \((y_1, y_2, \cdots , y_k)\)(保证 \(x_i \le y_i\))的方案数可以用组合数计算,类比二维情况,将路径看成每个方向的序列,求序列有多少种。那么方案数显然是下面这个式子
\[ \prod_{i=1}^k C_{\sum_{j=i}^k y_j - x_j}^{y_j - x_j} \]
方便起见,令 \(\Delta x_i = y_i - x_i\),我们将上式的组合数展开,得到
\[ \prod_{i=1}^k \frac{(\sum_{j=i}^k \Delta x_j)!}{\Delta x_i! \cdot (\sum_{j=i+1}^k \Delta x_j)!} \= \frac{(\Delta x_1 + \Delta x_2 + \cdots + \Delta x_k)!}{\Delta x_1! (\Delta x_2 + \Delta x_3 + \cdots + \Delta x_k)!} \cdot \frac{(\Delta x_2 + \Delta x_3 + \cdots + \Delta x_k)!}{\Delta x_2! (\Delta x_3 + \Delta x_4 + \cdots + \Delta x_k)!} \cdots \frac{\Delta x_k!}{\Delta x_k!} \= \frac{(\sum_{i=1}^k \Delta x_i)!}{\prod_{i=1}^k \Delta x_i!} \]
变成了一个非常简洁的形式!
下面还是考虑容斥,并尝试利用“坐标非常特殊”这种条件。注意:接下来将大量用到上面推到过的式子。
令 \(f(i)\) 表示只考虑 \((1, 1, \cdots , 1), (2, 2, \cdots, 2), \cdots , (n, n, \cdots, n)\) 那些点不能经过,从原点到 \((i, i, \cdots , i)\) 的方案数,那么 \(f(i) = \frac{(ki)!}{(i!)^k} - \sum_{j=1}^{i-1} { f(j) \frac{[k(i-j)]!}{[(i-j)!]^k} }\)。
令 \(g(i)\) 表示从原点到 \((a_1+i-n, a_2+i-n, \cdots , a_k+i-n)\),不经过所有不合法点的方案数,令 \(A = \sum_{i=1}^k a_i\),那么 \(g(i) = \frac{[A+k(i-n)]!}{\prod_{j=1}^k (a_j + i - n)!} - \sum_{j=1}^i { f(j) \frac{[A+k(i-j-n)]!}{\prod_{t=1}^k (a_t + i - j - n)!} } - \sum_{j=0}^{i-1} {g(j) h(i-j)}\)。注意,这里的容斥其实是所有方案依次减去经过的最小不合法点编号为 \(i\) 的方案,并且现在的编号是过原点的那条直线在前,过终点的那条直线在后,所以这就解释了那个函数 \(h(i)\) 是要干什么用的:它就是要求过终点的那条直线上的两个点之间的,不经过过原点那条直线上的点的路径数。
现在再考虑一下 \(h(i)\) 怎么求,其实就是一个各维度棱长为 \(i\) 的超立方体,从左下角到右上角,不经过 \((m-n+i, m-n+i, \cdots , m-n+i)\)(\(m = \max \{ a_i \}\)) 这种点的路径数。这个东西需要再套一个容斥(雾):\(h(i) = \frac{(ki)!}{(i!)^k} - \sum_{j=0}^i { t(j) \frac{[A+k(i-j-n)]!}{\prod_{t=1}^k (a_t + i-j - n)!} }\)。
\(t(i)\) 就是从 \((0, 0, \cdots , 0)\) 到 \((m-n+i, m-n+i, \cdots , m-n+i)\),不经过 \((m-n+j, m-n+j, \cdots , m-n+j), j < i\) 的方案数。\(t(i) = \frac{[k(i+n)-A]!}{\prod_{j=1}^k (i+n-a_j)!} - \sum_{j=1}^{i=1} { t(j) \frac{[k(i-j)]!}{[(i-j)!]^k} }\),特别地,当 \(i < m-n\) 时,\(t(i) = 0\)。
以上式子看不懂属于正常现象,这种东西自己手推比较好。核心就是容斥。
于是发现上面四种 dp 值的转移都是卷积的形式,那么可以用分治 FFT 或多项式逆元来求了。个人认为多项式逆元好一些,只需要推下式子,好写,复杂度还低。
下面令 \(F(x), G(x), H(x), T(x)\) 分别为 \(f(i), g(i), h(i), t(i)\) 的生成函数;并令 \(T_1(x) = \sum_{i=0}^n { \frac{(ki)!}{(i!)^k} x^i }, T_2(x) = \sum_{i=0}^n { \frac{[A+k(i-n)]!}{\prod_{j=1}^k (a_j+i-n)!} x^i }, T_3(x) = \sum_{i=0}^n { \frac{[k(i+n)-A]!}{\prod_{j=1}^k (i+n-a_j)!} [i \ge m-n] x^i }\)(对应着三个广义组合数)。那么可以退一下式子求解出 \(F(x), G(x), H(x), T(x)\)。
\[ F(x): \T_1(x) = F(x)T_1(x) + 1 \F(x) = \frac{T_1(x) - 1}{T_1(x)} \]
\[ G(x): \T_2(x) = F(x)T_2(x) + G(x)H(x) \G(x) = \frac{[1-F(x)]T_2(x)}{H(x)} \]
\[ T(x): \T(x) = \frac{T_3(x)}{T_1(x)} \]
\[ H(x): \H(x) = T_1(x) - T(x)T_2(x) \]
最后 \(g(n)\) 就是答案。
force:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = getchar(); }
return x * f;
}
#define maxd 110
#define maxn 2010
#define maxtot 201010
#define oo 2147483647
#define MOD 998244353
#define LL long long
int k, n, a[maxd], f[maxn], g[maxn], t[maxn], h[maxn], T[maxn], T2[maxn], T3[maxn], fac[maxtot], ifac[maxtot];
int Pow(int a, int b) {
int ans = 1, t = a;
while(b) {
if(b & 1) ans = (LL)ans * t % MOD;
t = (LL)t * t % MOD; b >>= 1;
}
return ans;
}
int main() {
k = read(); n = oo;
int A = 0, mxa = 0;
rep(i, 1, k) a[i] = read(), A += a[i], n = min(n, a[i]), mxa = max(mxa, a[i]);
ifac[1] = 1;
rep(i, 2, A) ifac[i] = (LL)(MOD - MOD / i) * ifac[MOD%i] % MOD;
fac[0] = ifac[0] = 1;
rep(i, 1, A) fac[i] = (LL)fac[i-1] * i % MOD, ifac[i] = (LL)ifac[i] * ifac[i-1] % MOD;
rep(i, 0, n) {
T[i] = (LL)fac[k*i] * Pow(ifac[i], k) % MOD;
T2[i] = fac[A+k*(i-n)];
rep(j, 1, k) T2[i] = (LL)T2[i] * ifac[a[j]+i-n] % MOD;
T3[i] = fac[k*(i+n)-A];
rep(j, 1, k) T3[i] = (LL)T3[i] * ifac[i+n-a[j]] % MOD;
// printf("Ts[%d] %d %d %d\n", i, T[i], T2[i], T3[i]);
}
rep(i, 1, n) {
f[i] = T[i];
rep(j, 1, i - 1) {
f[i] -= (LL)f[j] * T[i-j] % MOD;
if(f[i] < 0) f[i] += MOD;
}
}
rep(i, 0, n) {
h[i] = T[i];
if(i >= mxa - n) {
t[i] = T3[i];
rep(j, 1, i - 1) {
t[i] -= (LL)t[j] * T[i-j] % MOD;
if(t[i] < 0) t[i] += MOD;
}
rep(j, mxa - n, i) {
h[i] -= (LL)t[j] * T2[i-j] % MOD;
if(h[i] < 0) h[i] += MOD;
}
}
else t[i] = 0;
}
rep(i, 0, n) {
g[i] = T2[i];
rep(j, 1, i) {
g[i] -= (LL)f[j] * T2[i-j] % MOD;
if(g[i] < 0) g[i] += MOD;
}
rep(j, 0, i - 1) {
g[i] -= (LL)g[j] * h[i-j] % MOD;
if(g[i] < 0) g[i] += MOD;
}
}
/*rep(i, 0, n) printf("f[%d] = %d\n", i, f[i]);
rep(i, 0, n) printf("h[%d] = %d\n", i, h[i]);
rep(i, 0, n) printf("t[%d] = %d\n", i, t[i]);
rep(i, 0, n) printf("g[%d] = %d\n", i, g[i]); // */
printf("%d\n", g[n]);
return 0;
}100pts:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 524288
#define MOD 998244353
#define Groot 3
#define LL long long
int Pow(int a, int b) {
int ans = 1, t = a;
while(b) {
if(b & 1) ans = (LL)ans * t % MOD;
t = (LL)t * t % MOD; b >>= 1;
}
return ans;
}
int brev[maxn];
void FFT(int *a, int len, int tp) {
int n = 1 << len;
rep(i, 0, n - 1) if(i < brev[i]) swap(a[i], a[brev[i]]);
rep(i, 1, len) {
int wn = Pow(Groot, MOD - 1 >> i);
if(tp < 0) wn = Pow(wn, MOD - 2);
for(int j = 0; j < n; j += 1 << i) {
int w = 1;
rep(k, 0, (1 << i >> 1) - 1) {
int la = a[j+k], ra = (LL)w * a[j+k+(1<<i>>1)] % MOD;
a[j+k] = (la + ra) % MOD;
a[j+k+(1<<i>>1)] = (la - ra + MOD) % MOD;
w = (LL)w * wn % MOD;
}
}
}
if(tp < 0) {
int invn = Pow(n, MOD - 2);
rep(i, 0, n - 1) a[i] = (LL)a[i] * invn % MOD;
}
return ;
}
void Mul(int *A, int *B, int n, int m, bool recover = 0) {
int N = 1, len = 0;
while(N <= n + m) N <<= 1, len++;
rep(i, 0, N - 1) brev[i] = (brev[i>>1] >> 1) | ((i & 1) << len >> 1);
FFT(A, len, 1); FFT(B, len, 1);
rep(i, 0, N - 1) A[i] = (LL)A[i] * B[i] % MOD;
FFT(A, len, -1); if(recover) FFT(B, len, -1);
return ;
}
int tmp[maxn];
void inverse(int *f, int *g, int n) {
if(n == 1) return (void)(f[0] = Pow(g[0], MOD - 2));
inverse(f, g, n + 1 >> 1);
rep(i, 0, n - 1) tmp[i] = g[i];
int N = 1, len = 0;
while(N <= (n << 1)) N <<= 1, len++;
rep(i, 0, N - 1) brev[i] = (brev[i>>1] >> 1) | ((i & 1) << len >> 1);
rep(i, n, N - 1) tmp[i] = f[i] = 0;
FFT(f, len, 1); FFT(tmp, len, 1);
rep(i, 0, N - 1) f[i] = (LL)f[i] * (2ll - (LL)tmp[i] * f[i] % MOD + MOD) % MOD;
FFT(f, len, -1); rep(i, n, N - 1) f[i] = 0;
return ;
}
#define maxd 110
#define maxtot 20000010
#define oo 2147483647
int k, a[maxd], fac[maxtot], ifac[maxtot];
int F[maxn], G[maxn], T[maxn], H[maxn], T1[maxn], T2[maxn], T3[maxn];
int main() {
int n = oo, A = 0, mxa = 0;
k = read();
rep(i, 1, k) a[i] = read(), A += a[i], n = min(n, a[i]), mxa = max(mxa, a[i]);
ifac[1] = 1;
rep(i, 2, A) ifac[i] = (LL)(MOD - MOD / i) * ifac[MOD%i] % MOD;
fac[0] = ifac[0] = 1;
rep(i, 1, A) fac[i] = (LL)fac[i-1] * i % MOD, ifac[i] = (LL)ifac[i] * ifac[i-1] % MOD;
rep(i, 0, n) {
T1[i] = (LL)fac[k*i] * Pow(ifac[i], k) % MOD;
T2[i] = fac[A+k*(i-n)];
rep(j, 1, k) T2[i] = (LL)T2[i] * ifac[a[j]+i-n] % MOD;
T3[i] = i < mxa - n ? 0 : fac[k*(i+n)-A];
rep(j, 1, k) T3[i] = (LL)T3[i] * ifac[i+n-a[j]] % MOD;
}
inverse(F, T1, n + 1);
T1[0]--;
Mul(F, T1, n, n, 1);
T1[0]++;
rep(i, n + 1, n << 1) F[i] = 0;
inverse(T, T1, n + 1);
Mul(T, T3, n, n, 1);
rep(i, n + 1, n << 1) T[i] = 0;
memcpy(H, T, sizeof(T));
Mul(H, T2, n, n, 1);
rep(i, n + 1, n << 1) H[i] = 0;
rep(i, 0, n) H[i] = (T1[i] - H[i] + MOD) % MOD;
inverse(G, H, n + 1);
rep(i, 0, n) F[i] = MOD - F[i]; F[0]++;
Mul(F, T2, n, n);
rep(i, n + 1, n << 1) F[i] = 0;
Mul(G, F, n, n);
printf("%d\n", G[n]);
return 0;
}C 角点检测
乱搞题,不是用来 AC 的,有兴趣的同学可以自学图像处理。
