参考：https://www.cnblogs.com/pinard/p/6251584.html
定义：
SVD用于对矩阵进行分解，假设待分解矩阵A大小为m×n的矩阵，那么矩阵A的SVD为：
以上的U是一个mxm的矩阵，Σ是一个mxn的矩阵，除了主对角线意外其他值均为0，主对角线上每个元素均为奇异值，V是一个nxn的矩阵，且U和V均满足
.
下面则介绍如何求得U、Σ、V的过程。
我们将A的转置和A作矩阵相乘，那么得到nxn的方阵
，由于这是一个方阵，那么我们可以进行特征分解，得到特征值和特征向量满足下式子：
这样我们则得到
的特征值和对应的特征向量，将特征向量组成一个nxn的矩阵，那么就得到SVD公式的V矩阵，一般将V的每个特征向量叫做A的右奇异向量。
若将A和A的转置作矩阵相乘，那么得到mxm的矩阵
，同样进行特征分解，得到如下的特征值和特征向量：
这样则得到对应的m个特征向量u和m个特征值，将的所有特征向量组成一个mxm的特征矩阵U，那么就能得到SVD矩阵里的U矩阵，一般我们将U中的每个特征向量称为A的左奇异向量。
剩下的求奇异值矩阵Σ过程，由于其除了对角线上的奇异值之外其他都是0，那么我们只需要求出对应的奇异值σ即可。
由于：
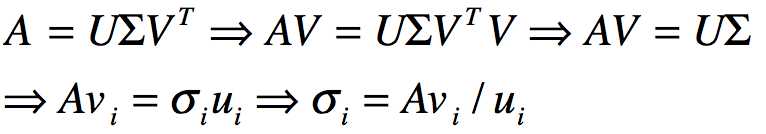
那么我们就可以得到各奇异值，进而得到奇异矩阵Σ.
判断和得到的特征向量组成的矩阵分别为V矩阵和U矩阵，以如下为例(ΣT=Σ)：
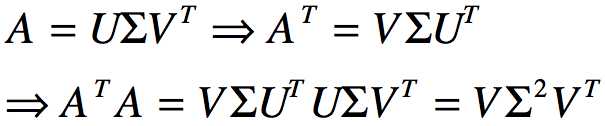
从而发现的特征向量组成的就是SVD分解中的V矩阵，同理可以得到的特征向量组成的就是SVD分解中的U矩阵，进一步可以发现特征值矩阵为奇异值矩阵的平方，
也即奇异值和特征值满足如下关系：
