AGC017 F - Zigzag

Problem Statement

There are N(N+1)?2 dots arranged to form an equilateral triangle whose sides consist of N dots, as shown below. The j-th dot from the left in the i-th row from the top is denoted by (i,j) (1≤i≤N, 1≤j≤i). Also, we will call (i+1,j) immediately lower-left to (i,j), and (i+1,j+1) immediately lower-right to (i,j).

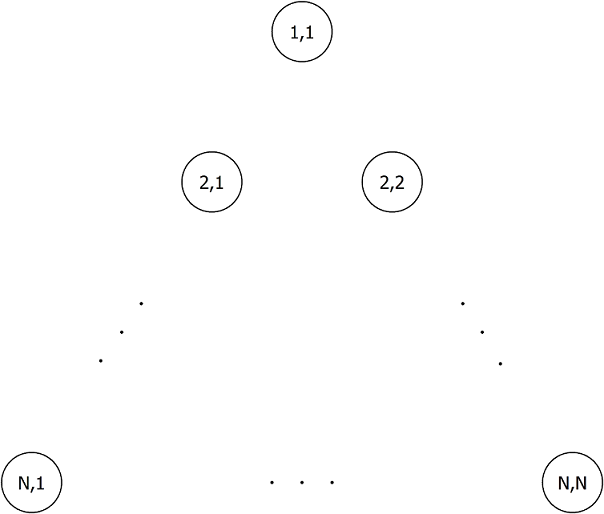
Takahashi is drawing M polygonal lines L₁,L₂,…,L_M by connecting these dots. Each L_i starts at (1,1), and visits the dot that is immediately lower-left or lower-right to the current dots N?1 times. More formally, there exist X_i,1,…,X_i,N such that:

• L_i connects the N points (1,X_i,1),(2,X_i,2),…,(N,X_i,N), in this order.
• For each j=1,2,…,N?1, either X_i,j+1=X_i,j or X_i,j+1=X_i,j+1 holds.

Takahashi would like to draw these lines so that no part of L_i+1 is to the left of L_i. That is, for each j=1,2,…,N, X_1,j≤X_2,j≤…≤X_M,j must hold.

Additionally, there are K conditions on the shape of the lines that must be followed. The i-th condition is denoted by (A_i,B_i,C_i), which means:

• If C_i=0, L_Ai must visit the immediately lower-left dot for the B_i-th move.
• If C_i=1, L_Ai must visit the immediately lower-right dot for the B_i-th move.

That is, X_Ai,Bi+1=X_Ai,Bi+C_i must hold.

In how many ways can Takahashi draw M polygonal lines? Find the count modulo 1000000007.

Notes

Before submission, it is strongly recommended to measure the execution time of your code using "Custom Test".

Constraints

• 1≤N≤20
• 1≤M≤20
• 0≤K≤(N?1)M
• 1≤A_i≤M
• 1≤B_i≤N?1
• C_i=0 or 1
• No pair appears more than once as (A_i,B_i).

Sample Input 1

3 2 1
1 2 0

Sample Output 1

6

There are six ways to draw lines, as shown below. Here, red lines represent L₁, and green lines represent L₂.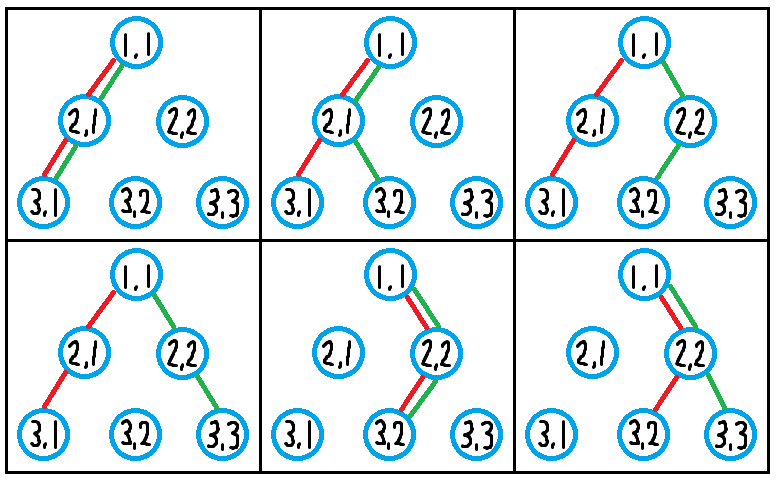

Sample Input 2

3 2 2
1 1 1
2 1 0

Sample Output 2

0

Sample Input 3

   5 4 2

   1 3 1

   4 2 0

Sample Output 4

881396682

题目大意
有一高度为N的三角形，共有M条线从顶部走到底部，要求第L+1条线不能在第L条线的左边，有K个要求，要求第a条线必须在第b层向某方向走（c为一即向左，为二则向右），问共有几种情况
分析
轮廓线DP
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
int dp[1048580];
int need1[21],need2[21];
int put[1048580],go[1048580][21];
//go是记录将一条先向左再向右边翻折后的形状
//put记录一直延左走的第一个与其他线相交的点
int n,m,k;
int main()
{     int i,j,p,q,a,b,c;
      scanf("%d%d%d",&n,&m,&k);
      for(i=1;i<=k;i++){
          scanf("%d%d%d",&a,&b,&c);
          a--,b--;
          need1[a]|=(1<<b);
          need2[a]|=(1<<b)*c;
      }
      n--;
      memset(go,-1,sizeof(go));
      memset(put,-1,sizeof(put));
      for(i=0;i<(1<<n);i++){
           int num=0;
         for(j=0;j<n;j++)
            if(i&(1<<j)){
              if(j>0&&!(i&(1<<(j-1)))){
                go[i][num]=i^(1<<j)^(1<<(j-1));
                //i指路径，num指第几个向右
              }
              num++;
            }
      }
      for(i=0;i<(1<<n);i++)
         for(j=n-1;j>=0;j--){
            if((i&(1<<j)))continue;
            put[i]=i^(1<<j);
            break;
         }
      dp[0]=1;
      for(i=0;i<m;i++){
         for(j=0;j<(1<<n);j++)
            if(put[j]){
              dp[put[j]]+=dp[j];
              dp[put[j]]%=1000000007;
         }
         for(p=0;p<n;p++)
            for(j=(1<<n)-1;j>=0;j--)
               if(go[j][p]!=-1){
                 dp[go[j][p]]+=dp[j],
                 dp[go[j][p]]%=1000000007;
               }
         for(j=0;j<(1<<n);j++)
            if((j&need1[i])!=need2[i])
              dp[j]=0;
      }
      int ans=0;
      for(i=0;i<(1<<n);i++)
         ans+=dp[i],
         ans%=1000000007;
      printf("%d\n",ans%1000000007);
      return 0;
}