表示图的三种方法

（原址）

三标准：

• 图结构占用的空间
• 确定图的一条给定边界花费的时间
• 从给定节点处找到邻居花费的时间

Edge List

• 以[v,w]为元素的列表，其中v，w为节点编号，每个元素表示一条边；
• 如果有权重，则元素形式为[v,w,k]
• 缺点：搜索某一特定边缘，必须进行遍历，最坏情况需要遍历完整个列表（不满足标准2）
  表示方法：
  [ [0,1], [0,6], [0,8], [1,4], [1,6], [1,9], [2,4], [2,6], [3,4], [3,5], [3,8], [4,5], [4,9], [7,8], [7,9] ]

Adjacency Matrices（邻接矩阵）

• 若图有V个节点，那么图的邻接矩阵为V*V大小。
• 若边界(i,j)存在，则对应矩阵元素值为1，否则为0。
• 如果有权重，矩阵元素值为权重，可能为null
• 无向图的邻接矩阵是对称的；有向图的邻接矩阵无需对称。
• 缺点1：所需存储空间大（特别是在稀疏图中）

• 缺点2: 搜索给定顶点的邻居时需要遍历一整行的V个节点（特别是邻居稀少时），花费的时间多，得到的结果少。
  
  表示方法：

  [ [0, 1, 0, 0, 0, 0, 1, 0, 1, 0],
    [1, 0, 0, 0, 1, 0, 1, 0, 0, 1],
    [0, 0, 0, 0, 1, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 1, 1, 0, 0, 1, 0],
    [0, 1, 1, 1, 0, 1, 0, 0, 0, 1],
    [0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
    [1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 0],
    [0, 1, 0, 0, 1, 0, 0, 1, 0, 0] ]

Adjacency Lists （邻接列表）

• 对于每个顶点，拥有一个邻接列表，包含所有邻居节点。

• 如果有权重，邻接列表中每个元素由两个数组成：顶点，权重
  
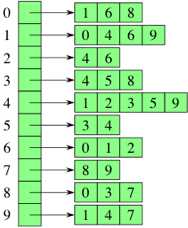
  表示方法：

  [ [1, 6, 8],
    [0, 4, 6, 9],
    [4, 6],
    [4, 5, 8],
    [1, 2, 3, 5, 9],
    [3, 4],
    [0, 1, 2],
    [8, 9],
    [0, 3, 7],
    [1, 4, 7] ]