<图像理解> 2-空间推理和基于模型的图像理解

1 - 关于空间实体和空间关系的知识表示和推理：

在AI领域

　　- 主要是拓扑关系

　　- formal 逻辑 meretopology

　　- 推理

在图像解释方面欠发达

　　- 需要不精确的只是表示

　　- 半量化框架->数值评估

　　- 例如 在非清晰图像中的结构识别

主要成分

　　- 知识表示 包含空间关系

　　- 不精确的表示与管理

　　- 异构信息的融合

　　- 推理和决策

2 - 语言学：

不同语言描述实体的空间位置是不同的，同一个单词表达的意思是不一样的，例如德语中path

根据上下文，根据reference得到物体实体的功能特性

不精确，若有很多非常复杂的信息，过于精确的陈述会变的不太现实

3- 人类感知：关于距离的例子：

　　- 纯粹的空间measure：在几何意义上即度量距离，与物体的固有属性有关

　　- 实践性的measure：用旅行时间表示的距离，是外在类型，和前一类纯粹空间是相反的

　　- 经济measure：是指投资成本，外在类型

　　- 感知性measureL导致指示类型的距离，和外部观点有关，即心理，可能受到环境的影响，通过主管考虑，导致距离并不一定是对称的

　　- 其他物体的影响

4 - 认识：

对空间环境的认识理解来自两种类型的过程

　　- 路线知识获取：儿童发展时期习得，意味着访问过的地标之间的顺序信息

　　- 调查知识获取：例如从地图上，看到全球的视图，与地表之间的顺序无关

5 - 空间推理形式：

　　- 定量

　　- 定性

　　- 模糊fuzzy表示和推理：半定量半定性

　　- 空间实体

　　- 空间关系

　　- 真实世界的问题：解决不精确性和不确定性

6 - 空间实体：

　　- 区域region，和模糊的区域fuzzy region

　　- key points 关键点

　　- 简化区域：例如质心：centroide，bounding box 关于边界框 详见：http://blog.csdn.net/zijin0802034/article/details/77685438

　　- 抽象表示 例如mereotopology 分体拓扑学

7 - 空间关系

　　- 结构稳定性 比形状 大小绝对位置稳定

　　- 不同的类型：binary n ary 等等

8 - 定量表示：quantitative

　　- 更精确的定义对象

　　- 计算已经定义好的关系

　　- 有许多限制：物体，关系，表示的类型

　　- 并不总是和通常的推理方式相匹配

9 - 定性：符号表示

　　主要的特征：

　　- 形式逻辑：命题，一阶……

　　- 对一类情况的完整性和复杂性之间的妥协 compromise

　　- 推理：可满足性 etc

小问题：

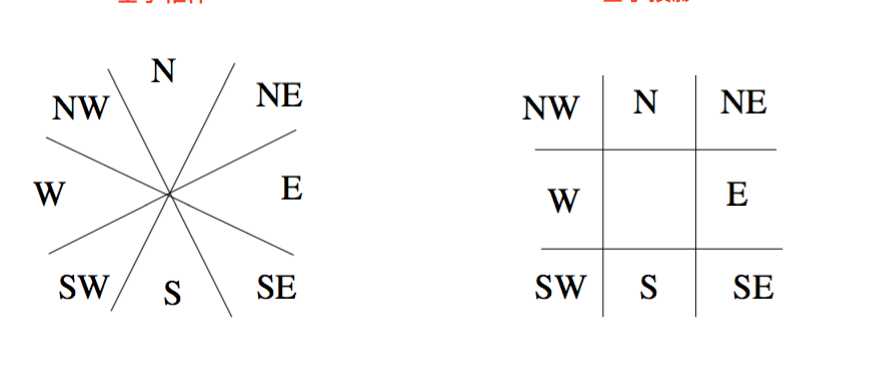
对于复杂的形状我们如何处理？只需要很少的部分可以被准确的确定。

我们可以使用bounding box 和 centroide

定性的几种方法

1 艾伦区间 allen‘s interval

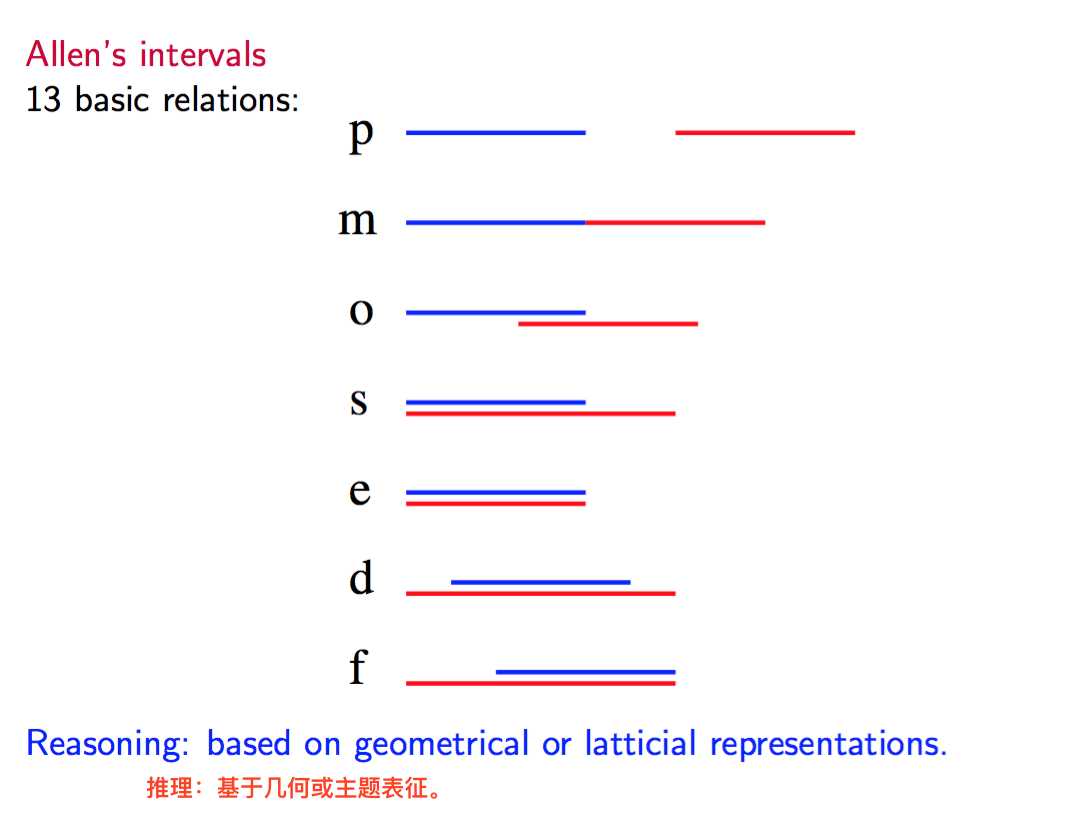
allen‘s intervals ：是时空推理计算。该代数定义了时间间隔之间的可能关系并提出了组合表。 它可以作为推理关于事件的时间描述的基础。

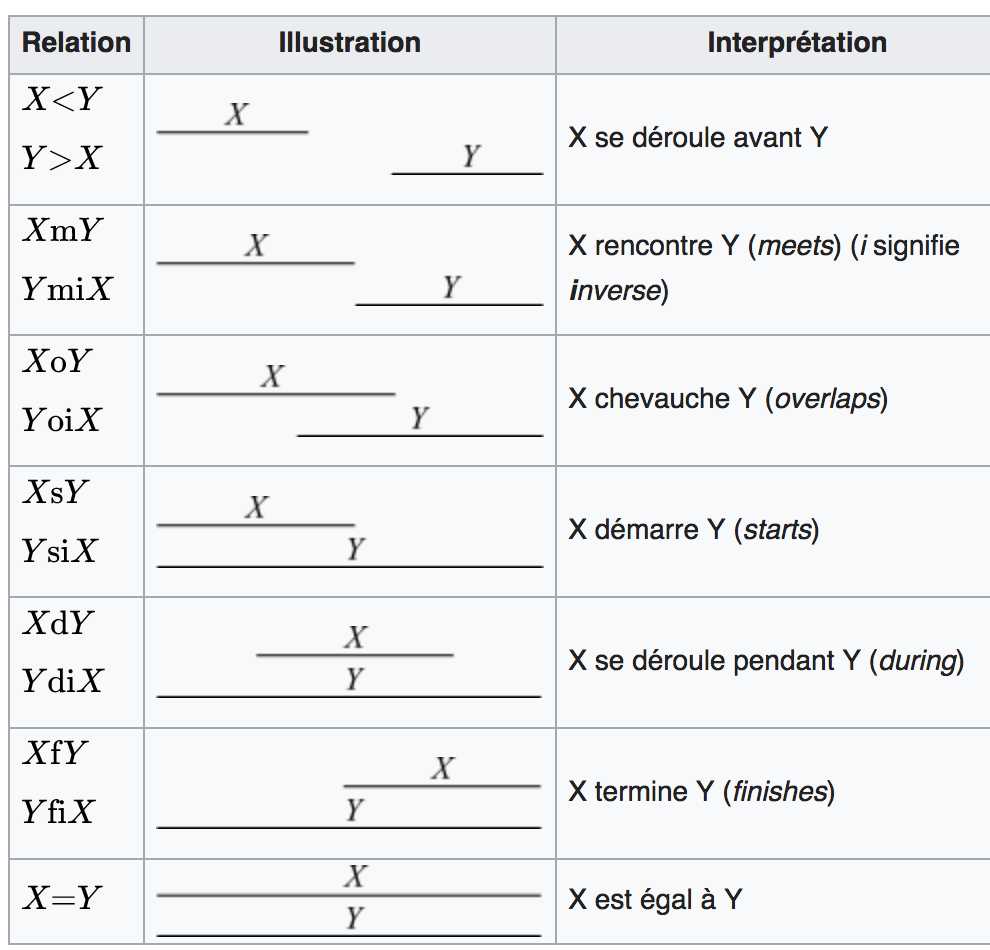
上面的表说明的是一维的情况，复杂度为13

若是二维，即是表格lattice的形式，复杂度为13的平方

若是三维，复杂度为13的三次方

所以这个方法的复杂度非常高，用于固定了形状的物体

2 RCC Region Connection calculs 区域连接演算

　　-用定性的方式，定义空间实体

　　- 没有参考点 reference points

　　- 连接谓词C

　　- 分段谓词P

　　公式：

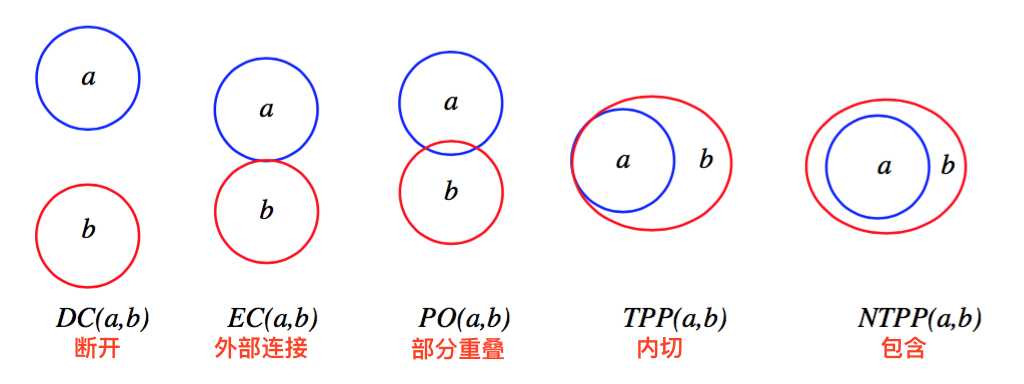
一些关系的表示

3 定性轨迹验算：

用RCC和艾伦的方法一起

例如：

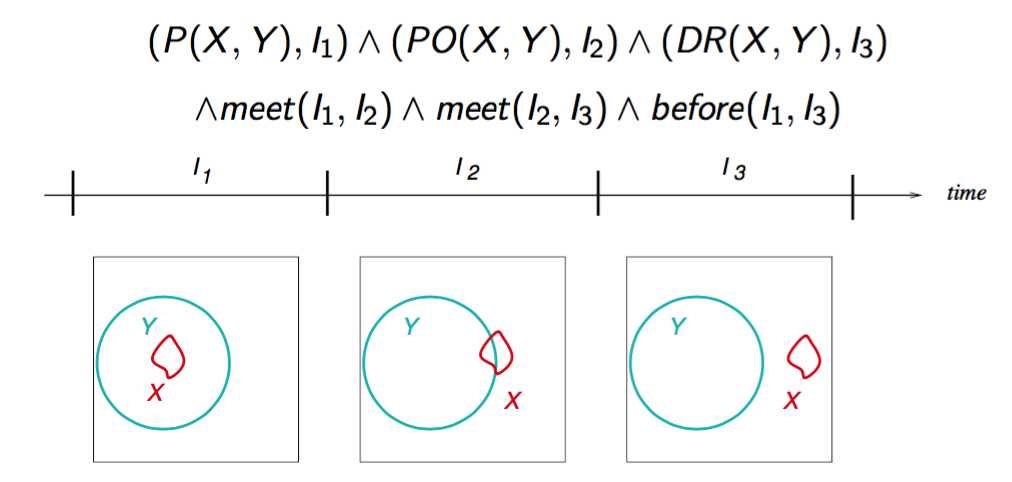
meet是指 I1时间段后面就能遇到I2，对I2 I3同理，那么I1在I3前面

P 是指X是Y的部分

PO X和Y相交一部分

DR X和Y完全分离开

9 - 空间的模态逻辑

□A 是指本地为真，即 如果A在x的邻域内是真的，那么A在点x上即为真

◇A = no □ no A ：是指如果A在x的邻域内的某一点为真，那么A在x上为真

□表示everywhere □A everywhere close to A

◇表示somewhere ◇A somewhere close to A

 

一些推理规则：

　　

 

 

 

10 - 半定量空间推理：模糊方法

　　- 纯定性推理的局限性

　　- 对于纯定性加入半定量扩展，可以活的更有用的结论

　　- 在不精确的陈述中使用纯量化表示限制，用语言表达的知识etc

　　- 使用模糊集的半定量或半定型解释来整合定量和定性的知识

　　- 模糊集合提供计算表示，不精确的空间约束的解释，用语言的方式表达，可能包括定量的知识

　　- 粒度

　　　　- 物体或空间实体和他们的描述

　　　　- 类型和空间关系及query的表达

　　　　- 预期或潜在的结果的类型

 

11 - 基于模型的识别和空间推理

　　- 不精确的表示

　　- 空间关系作为结构信息：拓扑关系，距离，相对方向关系relative directional relations，etc

　　- 两类关系

　　　　- 在清晰的情况下 crisp case，很好的定义 例如 邻接，距离

　　　　- 即使在清晰的情况下，各种 也是模糊vague的

　　- 多种异质知识和信息的片段的组合

--> 模糊集理论，数学形态学

 

12 - 不精确和模糊

　　- 物体：边界不清晰，粗分割 coarse segmentation

　　- 关系：很接近 quite close之类

　　- 可用知识的类型不清晰etc

　　- 问题回答的不清晰

13 - 模糊集定义　　

　　- 模糊集：给定一个空间S，从S到单位区间[0，1]的映射μA（x）：S→[0，1]，叫做S在U上的一个模糊集或者模糊子集

　　- μA（x）是隶属函数，表示元素对模糊集A的隶属程度

　　

 

 

 

14 - 一些运算

 

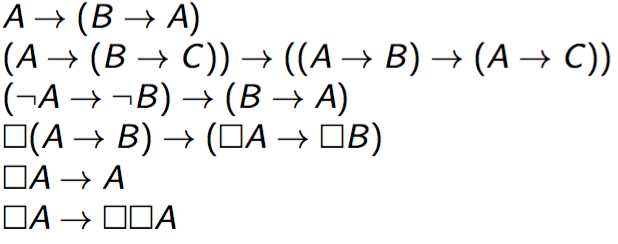
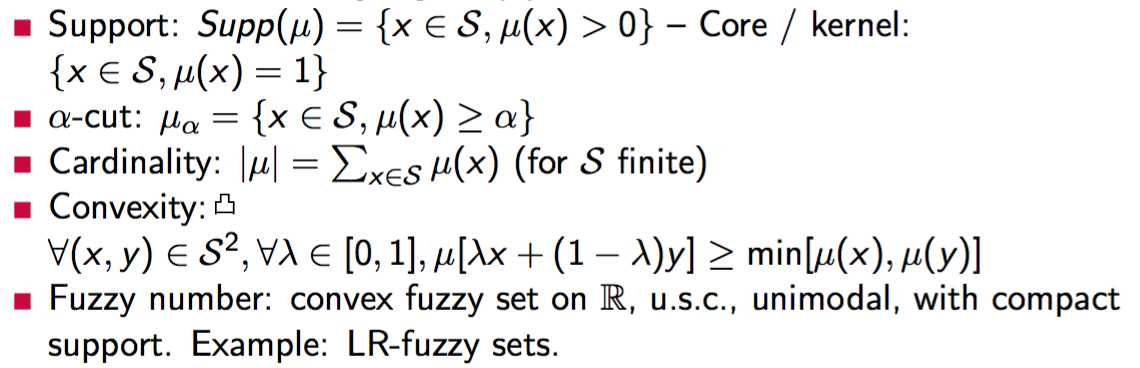
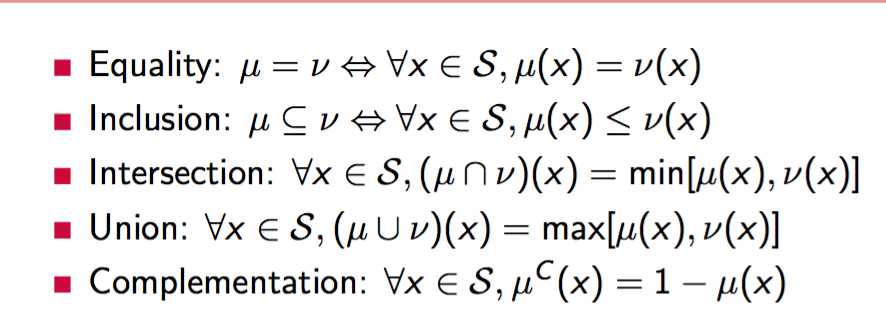
幂等idempotent：在编程中一个米等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同

15 - 语义

　　- 相似度：距离的概念

　　- 合理度 plausibility：一个不精确描述的对象实际上

　　- 偏好程度 接近效用函数的概念

16 - 不同类型的imperfection

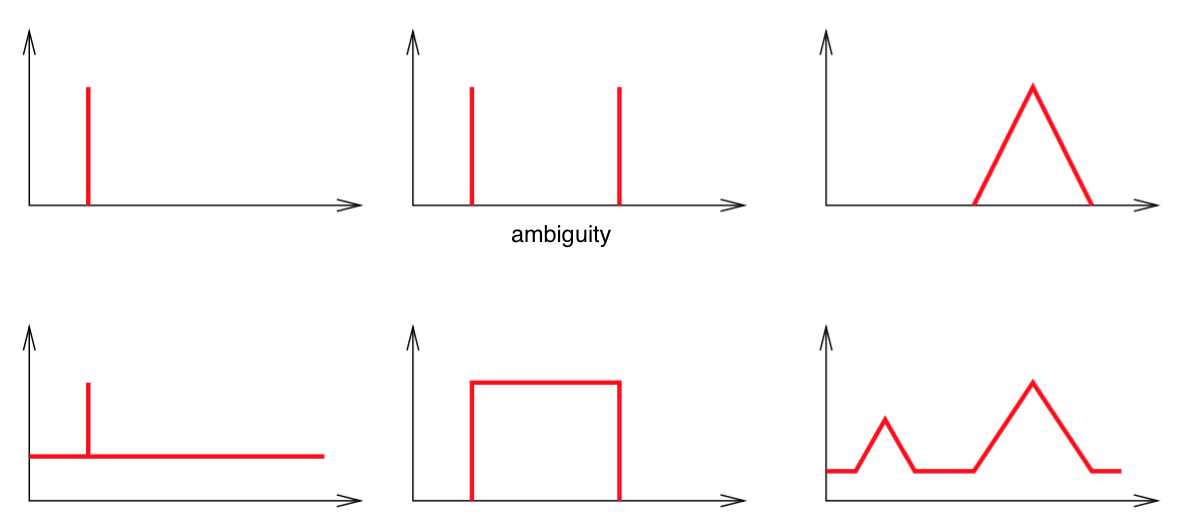
17 - 模糊互补

　　- 函数c从[0,1]到[0,1]，使得：c(0) = 1, c(1) = 0

　　- c是对合的，即对于所有x在 [0,1]，c（c（x））= x

　　- c是单调递减的

　　　连续补充的一般形式：c(x) = φ^-1[1-φ(x)]

　　φ： [0,1]→[0,1], φ(0) = 0, φ(1) = 1, φ是单调递增的

18 - 三角规范

　　三角规范 triangular norm (模糊相交 fuzzy interaction)

　　t-norm t : [0,1] * [0,1] -> [0,1]

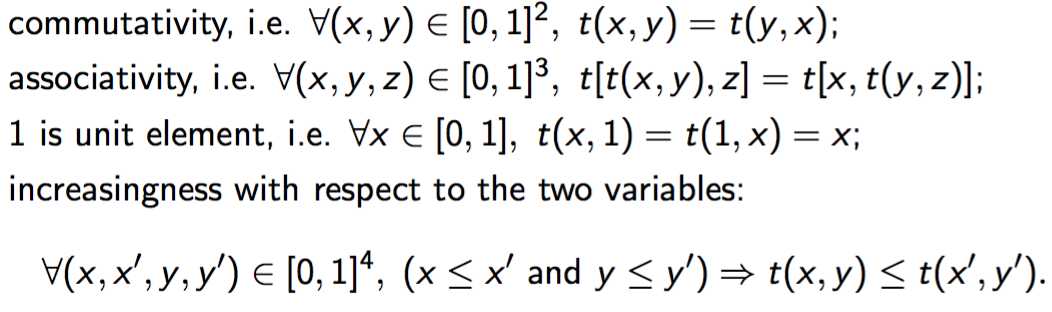
　　三角余范 Triangular conorms fuzzy union = t-conorm->disjunction

　　[0,1] * [0,1] -> [0,1]