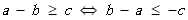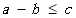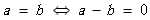题目描述
小 K 在 Minecraft 里面建立很多很多的农场,总共 n 个,以至于他自己都忘记了每个
农场中种植作物的具体数量了,他只记得一些含糊的信息(共 m 个),以下列三种形式描
述:
-
农场 a 比农场 b 至少多种植了 c 个单位的作物。
-
农场 a 比农场 b 至多多种植了 c 个单位的作物。
- 农场 a 与农场 b 种植的作物数一样多。
但是,由于小 K 的记忆有些偏差,所以他想要知道存不存在一种情况,使得农场的种
植作物数量与他记忆中的所有信息吻合。
输入输出格式
输入格式:从 farm.in 中输入数据
第一行包括两个整数 n 和 m,分别表示农场数目和小 K 记忆中的信息数目。
接下来 m 行:
如果每行的第一个数是 1,接下来有 3 个整数 a,b,c,表示农场 a 比农场 b 至少多种植
了 c 个单位的作物。
如果每行的第一个数是 2,接下来有 3 个整数 a,b,c,表示农场 a 比农场 b 至多多种植
了 c 个单位的作物。如果每行的第一个数是 3,家下来有 2 个整数 a,b,表示农场 a 终止的
数量和 b 一样多。
输出格式:输出到 farm.out 中
如果存在某种情况与小 K 的记忆吻合,输出“Yes”,否则输出“No”。
输入输出样例
3 3 3 1 2 1 1 3 1 2 2 3 2
Yes
说明
对于 100% 的数据保证:1 ≤ n,m,a,b,c ≤ 10000。
分析
这题的重点在于这三种给出的条件。
看到这三个式子其实差分约束已经很明显了,然后我们把这三个式子转换为图上边的形式。
读入a,b(,t):
- 农场a指向农场b,边权为-t
- 农场b指向农场a,边权为t
- 农场a与农场b之间边权为0的无向边
要判断一个差分约束建的图是否合理,方法就是找图中是否有负环。(因为若存在负环,那么最短路就不存在了。)判断负环比较有效的方法就是用DFS-SPFA来判断。其实就是把SPFA算法原本依赖的数据结构从队列改成了栈。
程序
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int MAXN = 10000 + 1, MAXM = 20000 + 1; 4 int c, x, y, n, m, t, EdgeCount, Head[MAXN]; 5 stack<int> S; 6 int vis[MAXN], dist[MAXN]; 7 bool flag, f[10005]; 8 struct edge 9 { 10 int Next, Aim, Weight; 11 }Edge[MAXM]; 12 void insert(int u, int v, int w) 13 { 14 Edge[++EdgeCount] = (edge){Head[u], v, w}; 15 Head[u] = EdgeCount; 16 } 17 void SPFA(int x) 18 { 19 vis[x] = 1; 20 for (int i = Head[x]; i; i = Edge[i].Next) 21 { 22 if (dist[x] + Edge[i].Weight < dist[Edge[i].Aim]) 23 { 24 dist[Edge[i].Aim] = dist[x] + Edge[i].Weight; 25 if (vis[Edge[i].Aim]) 26 { 27 flag = true; 28 return; 29 } 30 SPFA(Edge[i].Aim); 31 } 32 } 33 vis[x] = 0; 34 } 35 int main() 36 { 37 cin >> n >> m; 38 for (int i = 1; i <= m; i++) 39 { 40 cin >> c >> x >> y; 41 if (c == 1) 42 cin >> t, insert(x,y,-1*t); 43 if (c == 2) 44 cin >> t, insert(y,x,t); 45 if (c == 3) 46 insert(x,y,0), insert(y,x,0); 47 } 48 for (int i = 1; i <= n; i++) 49 if (!flag) 50 SPFA(i); 51 if (flag) 52 printf("No\n"); 53 else 54 printf("Yes\n"); 55 return 0; 56 }