题目背景
wzt在家里的地板上玩一套神犇牌积木
题目描述
由于wzt家并不是无穷大的,所以地板只有n×m个单位大,且恰好由n×m个1× 1的小格子组成。以整个地板左上角的格子作为原点(坐标为(1,1)),wzt会将p块积木随意的抛出落在地板上。积木是一个长方体(此题中认为所有积木的高均为1),保证积木落地时积木底面端点恰好落在格点上,底面棱恰好与小格子的边重合(通俗的说就是不会斜着落在地板上)
神犇牌积木的边具有极强的不会消除的黏性,即当一个积木落下碰到另一个物体后,其位置不会再改变。如下图所示
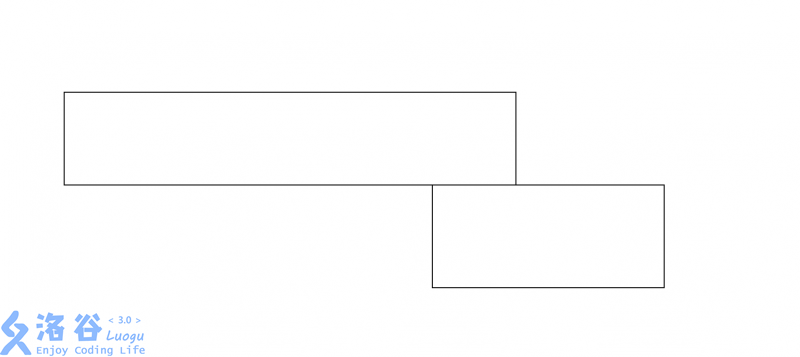
这种情况下,上方积木也不会斜着落下接触地面
就在wzt抛完了所有积木后,lsq突然来到他家。lsq突然问wzt
lsq:(用手一指)那个坐标上有几个积木?
wzt:……(数一数)5
lsq:(用手一指)那个坐标上有几个积木?
wzt:……(数一数)8
lsq:(用手一指)那个坐标上有几个积木?
wzt:………你怎么那么多问题……
lsq:不多啊,就q个而已。
wzt:………………
wzt对此感到很头疼,lsq的问题太多难了。于是他请求于AK过NOI的你帮他写一个程序解决这个问题
输入输出格式
输入格式:
第一行有两个数n,m,表示地板的大小
第二行有两个数p,q,表示p个积木和q个询问
接下来(p+q)行
前p行为p个积木的落地点,后q行为q个来自lsq的询问
格式:
a b x y:表示积木静止后左上端点为(a,b),右下端点为(x,y)
i j:表示lsq询问坐标为(i,j)的格子上有几个积木
输出格式:
输出共q行,为lsq的询问的答案
输入输出样例
说明
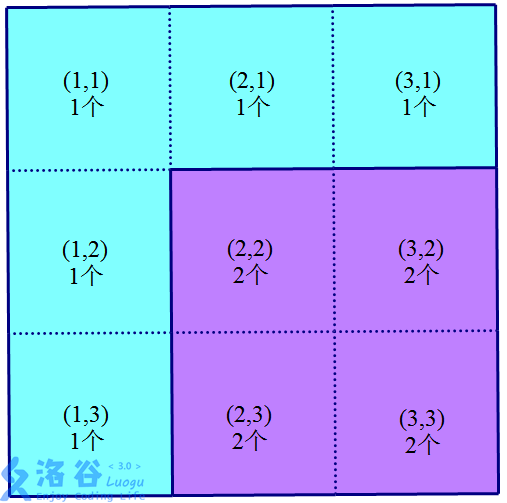
样例解释:
地毯可抽象成下图
保证所有积木的坐标均不超出地板范围,保证所有的ai<=xi,bi<=yi
对于30%的数据,n,m<=100,p,q<=500
对于60%的数据,n,m<=1000,p,q<=1000
对于100%的数据,n,m<=4000,p,q<=100000
洛谷公开赛,好坑,提交貌似迟了一分钟就没AC了……
如果说这题二维改成一维,那么每个人肯定都知道怎么做……差分!
那么二维是否也可以用差分呢?
答案是显然的。
不过顺序不一样,上下一起差分……看代码吧。
AC代码如下:
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=5000+5;
int sub[N][N],n,m,p,q,a,b,x,y;
int main()
{
scanf("%d%d%d%d",&n,&m,&p,&q);
for(int i=1;i<=p;i++)
{
scanf("%d%d%d%d",&a,&b,&x,&y);
sub[a][b]++,sub[x+1][b]--;
sub[a][y+1]--,sub[x+1][y+1]++;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
sub[i][j]+=sub[i][j-1];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
sub[i][j]+=sub[i-1][j];
for(int i=1;i<=q;i++)
scanf("%d%d",&x,&y),printf("%d\n",sub[x][y]);
return 0;
}
