伯努利数的应用

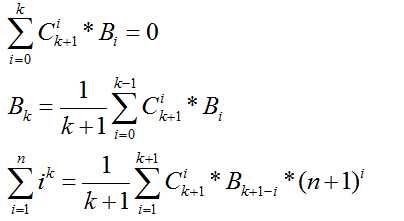
#include<cstdio>
typedef long long ll;
const int maxn=5005,mod=1e9+7;
int c[maxn][maxn],b[maxn],inv[maxn];
int T,k,tmp,ans;
ll n;
int main(){
	for(register int i=0;i<=5000;++i){
		c[i][0]=1;
		for(register int j=1;j<=i;++j)
			c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
	}
	inv[1]=1;
	for(register int i=2;i<=5000;++i)
		inv[i]=mod-1ll*mod/i*inv[mod%i]%mod;
	b[0]=1;
	for(register int i=1;i<=5000;++i){
		for(register int j=0;j<i;++j)
			b[i]=(b[i]+1ll*c[i+1][j]*b[j]%mod)%mod;
		b[i]=(mod-1ll*b[i]*inv[i+1]%mod)%mod;
	}
	scanf("%d",&T);
	while(T--){
		scanf("%lld%d",&n,&k);
		++n;
		n%=mod;
		tmp=n;
		ans=0;
		for(register int i=1;i<=k+1;++i,tmp=1ll*tmp*n%mod)
			ans=(ans+1ll*c[k+1][i]*b[k+1-i]%mod*tmp%mod)%mod;
		ans=1ll*ans*inv[k+1]%mod;
		printf("%d\n",ans);
	}
	return 0;
}

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int mod=998244353,maxn=2e5+5;
int a[maxn],b[maxn],tmp[maxn],s[maxn],gn[maxn],inv[maxn];
int n,k;
inline int fp(int a,int b){
	int ret=1;
	while(b){
		if(b&1)ret=1ll*a*ret%mod;
		a=1ll*a*a%mod;b>>=1;
	}
	return ret;
}
inline void ntt(int *a,int p,int f){
	for(register int i=0;i<p;++i)
		if(i<s[i])
			swap(a[i],a[s[i]]);
	for(register int i=1,t=0,g,w,v;i<p;i<<=1,++t){
		g=gn[t];
		for(register int j=0;j<p;j+=(i<<1)){
			w=1;
			for(register int k=j;k<i+j;++k,w=1ll*w*g%mod){
				v=1ll*w*a[i+k]%mod;
				a[i+k]=(a[k]-v+mod)%mod;
				a[k]=(a[k]+v)%mod;
			}
		}
	}
	if(f==1)return;
	reverse(a+1,a+p);
	int ny=fp(p,mod-2);
	for(register int i=0;i<p;++i)
		a[i]=1ll*a[i]*ny%mod;
}
inline void solve(int *b,int deg){
	if(deg==1){
		b[0]=fp(a[0],mod-2);
		return;
	}
	solve(b,(deg+1)>>1);
	int p=1,lg2=0;while(p<(deg<<1))p<<=1,++lg2;
	for(register int i=0;i<p;++i)tmp[i]=i<deg?a[i]:0;
	for(register int i=((deg+1)>>1);i<p;++i)b[i]=0;
	for(register int i=0;i<p;++i)s[i]=(s[i>>1]>>1)^((i&1)<<(lg2-1));
	ntt(tmp,p,1),ntt(b,p,1);
	for(register int i=0;i<p;++i)b[i]=(2ll*b[i]%mod-1ll*tmp[i]*b[i]%mod*b[i]%mod+mod)%mod;
	ntt(b,p,-1);
}
int main(){
	for(register int t=0,i=1;t<=20;i<<=1,++t)
		gn[t]=fp(3,(mod-1)/(i<<1));
	scanf("%d",&n);inv[1]=1;a[0]=1;
	for(register int i=2;i<=n+1;++i)inv[i]=mod-1ll*mod/i*inv[mod%i]%mod;
	for(register int i=1;i<=n;++i)a[i]=1ll*a[i-1]*inv[i+1]%mod;
	solve(b,n+1);
	for(register int i=0;i<=n;++i)printf("%d ",b[i]);
	return 0;
}