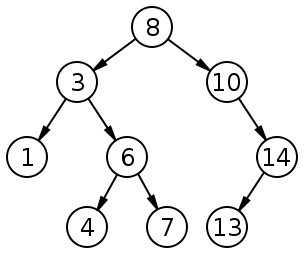
1. 二叉搜索树,又称BST。满足三个性质:
(1)若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)它的左、右子树也分别为二叉排序树。
2. 常用操作:
(1)中序遍历二叉排序树可得到一个有序序列。一个无序序列可以通过构造一棵二叉排序树变成一个有序序列,构造树的过程即是对无序序列进行排序的过程。
(2)每次插入的新的结点都是二叉排序树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。时间复杂度为O(h)。
3. 程序代码:
#include <iostream> #include <cstring> #include <vector> #include <memory> using namespace std; typedef struct node { int val; shared_ptr<node> left; shared_ptr<node> right; }Node; /*插入元素*/ bool insert(shared_ptr<node> &root, int ele) { if(root == NULL) //ele不存在与二叉树,创建一个节点并返回true { root = make_shared<node>(); root->val = ele; root->left = root->right = NULL; return true; } if(ele < root->val) { return insert(root->left, ele); } else if(ele > root->val) { return insert(root->right, ele); } else //ele已经存在于二叉树中,故返回false return false; } /*创建二叉搜索树*/ void creteBST(shared_ptr<node> &root, int vec[], int n) { root = NULL; for(int i=0; i<n; ++i) { insert(root,vec[i]); } } /*前序遍历*/ void PreOrderTraverse(shared_ptr<node> &root) { if(root != NULL) { cout<<root->val<<" "; PreOrderTraverse(root->left); PreOrderTraverse(root->right); } } /*中序遍历*/ void InOrderTraverse(shared_ptr<node> &root) { if(root != NULL) { InOrderTraverse(root->left); cout<<root->val<<" "; InOrderTraverse(root->right); } } int main() { int vec[10] = {4, 5, 2, 1, 0, 9, 3, 7, 6, 8}; shared_ptr<node> root = NULL; creteBST(root, vec, 10); PreOrderTraverse(root); cout<<endl; InOrderTraverse(root); return 0; }
