多元线性回归Linear Regression with multiple variables
当有一个特征输入时,h(x)函数可表示为
![]()
当有多个特征输入时,h(x)函数可表示为
![]()
设x0 = 1,则特征输入和参数可表示为:
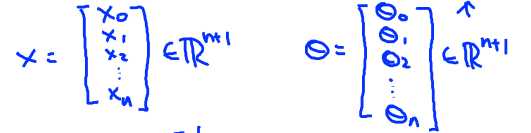
h(x)函数就可表示为:
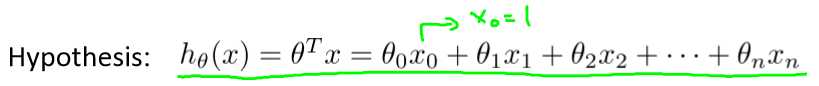
代价函数cost function:
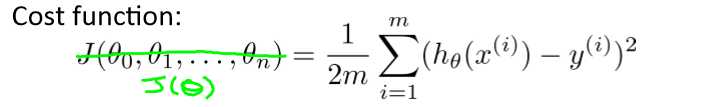
多元线性回归中的梯度下降

特征缩放Feature Scaling
当输入的特征值处在一个很大的范围时,梯度下降算法会迭代很多步才能达到收敛,
为了让收敛速度加快,我们时每一个特征值处在相同的范围,如-1到1内。
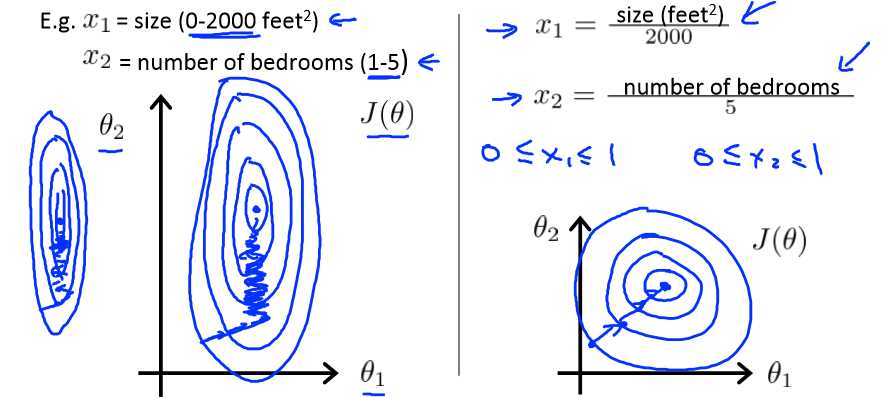
这个范围不应太大或太小,一般可取在-3到3。
均值归一化Mean Normalization
均值归一化就是用![]() 代替
代替![]() ,使xi的均值接近于0.但x0的值恒为1.
,使xi的均值接近于0.但x0的值恒为1.
学习速率α
为了确保梯度下降正常工作,可以作minJ(θ)关于迭代次数的函数图:
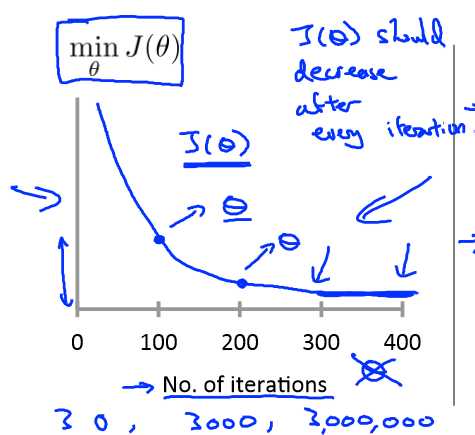 随着迭代次数的增加,minJ(θ)的值减小到趋于稳定,就说明梯度下降收敛。
随着迭代次数的增加,minJ(θ)的值减小到趋于稳定,就说明梯度下降收敛。
为了确保梯度下降正常工作,还可以用自动收敛测试,例如当minJ(θ)的值下降少于一个很小的值,如10-3时,可认为收敛,但这个值的大小不好选定。
几种可能出现的图像情况:

如果α的值过小,会收敛的很慢;
如果α的值过大,J的值可能在每一步迭代过程中不会减小,最终不会收敛。
为了选择合适的α,可以选择... 0.001,0.003,0.01,0.03,0.1,0.3,1 ...
特征值的选择
在建立函数h(x)时,不一定要将所有的特征值原封不动的写进去,可以对其进行组合,
如:一个用于房价预测的函数![]()
可令x=frontage*depth成为一个新的特征值,函数就变为![]()
标准方程法Normal equation
通过标准方程法可以通过一次计算得到θ值,而不需要像梯度下降那样做多次迭代,也不需要feature scaling。
公式:![]()
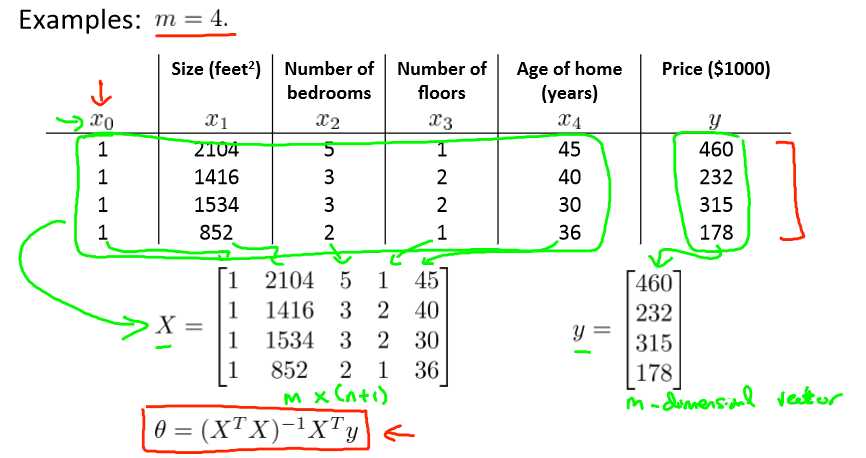
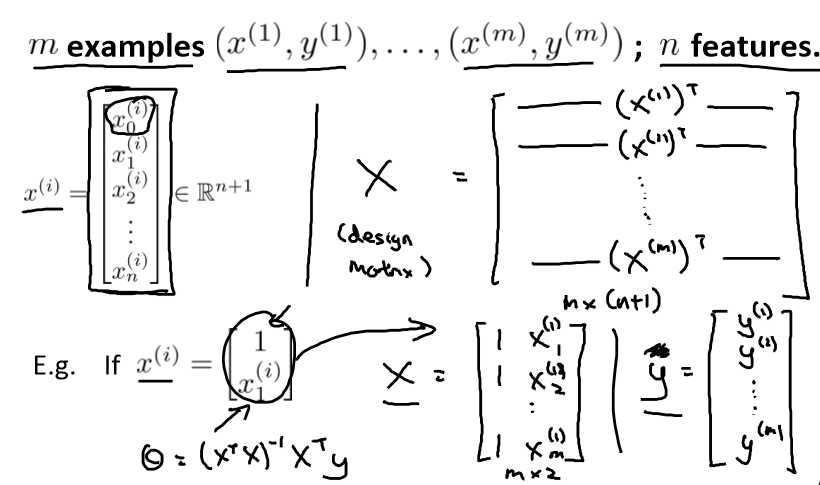
梯度下降法与标准方程法比较:
| 梯度下降法 | 标准方程法 |
| 需要选择α | 不需要选择α |
| 需要多次迭代 | 不需要迭代 |
| 当特征值个数n很大时,比较好 | 当特征值个数n很大时,运行较慢 |
| 当n=10000左右时,考虑用梯度下降 |
计算(XTX)-1需要O(n3) |
在运用标准方程法时可能会遇到XTX不可逆的情况,原因如下:
有冗余的特征值,例如两个特征值线性相关,这是需要删除冗余的特征值;
特征值太多,当样本数m<=特征值数n时,就可能导致不可逆。例如m=10,n=100,那么θ为101维,用10个样本来适配101个θ值,显然是不合适的。这种情况下需要删除一些特征值或利用正规化(regularization)。
