http://acm.hdu.edu.cn/showproblem.php?pid=3401
题意:
有一个股市,现在有T天让你炒股,在第i天,买进股票的价格为APi,卖出股票的价格为BPi,同时最多买进股票的数量为ASi,卖出股票的数量为BSi。一次交易之后要隔W天之后才能再次交易,并且手上最多持股maxP,问最多可以炒到多少钱。
思路:
首先列一个DP方程:
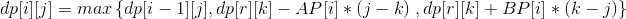
分别代表不买不卖,买进股票,卖出股票三种情况(上面 (j-k)<=AS[i] , (k-j)<=BS[i])。
那么这里需要枚举r和k的情况,由于相邻两次交易必须隔W天,也就是如果第i天交易了,那么至少要到第i+w+1天才能再次交易。如果我们在第i天要交易股票,那么前w天都是不买不卖的情况,那么前w天的情况都是一样的,所以这以r直接为i-w-1即可。
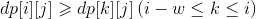
最后是将上面的式子化简一下:
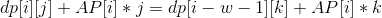
可以看见右边是与k有关的表达式,左边是与j有关的表达式,右边我们只需要选择最大的值即可,那么这就可以用单调队列来优化了。
以买股票为例子说明:
因为是买股票,所以j肯定是大于k的,所以j从小到大枚举。每次计算出右边的值,单调队列保存递减值。每次取队首的最大值,当然队首元素必须满足AS[i]的条件,不满足就出队列。
1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 const int maxn = 2000+5; 5 6 int t, maxp, w, ap[maxn], bp[maxn], as[maxn], bs[maxn], head, tail; 7 int dp[maxn][maxn]; 8 struct node 9 { 10 int p; 11 int x; 12 }q[maxn]; 13 14 int main() 15 { 16 //freopen("in.txt","r",stdin); 17 int T; 18 scanf("%d",&T); 19 while(T--) 20 { 21 scanf("%d%d%d",&t,&maxp,&w); 22 for(int i=1;i<=t;i++) 23 scanf("%d%d%d%d",&ap[i],&bp[i],&as[i],&bs[i]); 24 25 for(int i=0;i<=t;i++) 26 for(int j=0;j<=maxp;j++) 27 dp[i][j] = -0x3f3f3f3f; 28 29 for(int i=1;i<=w+1;i++) 30 for(int j=0;j<=as[i];j++) 31 dp[i][j] = -j*ap[i]; 32 33 for(int i=2;i<=t;i++) 34 { 35 for(int j=0;j<=maxp;j++) 36 dp[i][j] = max(dp[i][j],dp[i-1][j]); 37 if(i<=w+1) continue; 38 //买进 39 head = tail = 1; 40 for(int j=0;j<=maxp;j++) 41 { 42 int x = dp[i-w-1][j]+j*ap[i]; 43 while(head<tail && q[tail-1].x<x) tail--; 44 q[tail].x = x; 45 q[tail++].p = j; 46 while(head<tail && j-q[head].p>as[i]) head++; 47 dp[i][j] = max(dp[i][j], q[head].x-j*ap[i]); 48 } 49 50 //卖出 51 head = tail = 1; 52 for(int j=maxp;j>=0;j--) 53 { 54 int x = dp[i-w-1][j]+j*bp[i]; 55 while(head<tail && q[tail-1].x<x) tail--; 56 q[tail].x = x; 57 q[tail++].p = j; 58 while(head<tail && j+bs[i]<q[head].p) head++; 59 dp[i][j] = max(dp[i][j], q[head].x-j*bp[i]); 60 } 61 } 62 int ans = 0; 63 for(int i=0;i<=maxp;i++) 64 ans = max(ans,dp[t][i]); 65 printf("%d\n",ans); 66 } 67 return 0; 68 }
