前面我们学习过回归问题,比如对于房价的预测,因为其预测值是个连续的值,因此属于回归问题。
但还有一类问题属于分类的问题,比如我们根据一张图片来辨别它是一只猫还是一只狗。某篇文章的内容是属于体育新闻还是经济新闻等,这个结果是有一个全集的离散值,这类问题就是分类问题。
我有时会把回归问题看成是分类问题,比如对于房价值的预测,在实际的应用中,一般不需要把房价精确到元为单位的,比如对于均价,以上海房价为例,可以分为:5000-10万这样的一个范围段,并且以1000为单位就可以了,尽管这样分出了很多类,但至少也可以看成是分类问题了。
因此分类算法应用范围非常广泛,我们来看下在tensorflow中如何解决这个分类问题的。
本文用经典的手写数字识别作为案例进行讲解。
准备数据
# 准备数据
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets(‘D:/todel/python/MNIST_data/‘, one_hot=True)执行上述代码后,会从线上下载测试的手写数字的数据。
不过在我的机器上运行时好久都没有下载下相应的数据,最后我就直接到http://yann.lecun.com/exdb/mnist/ 网站上下载其中的训练数据和测试数据文件到指定的目录下,然后再运行这个程序就能把数据给解压开来。
这里总共大概有6万个训练数据,1万个测试数据。
手写数字是一堆28X28像素的黑白图片,例如:
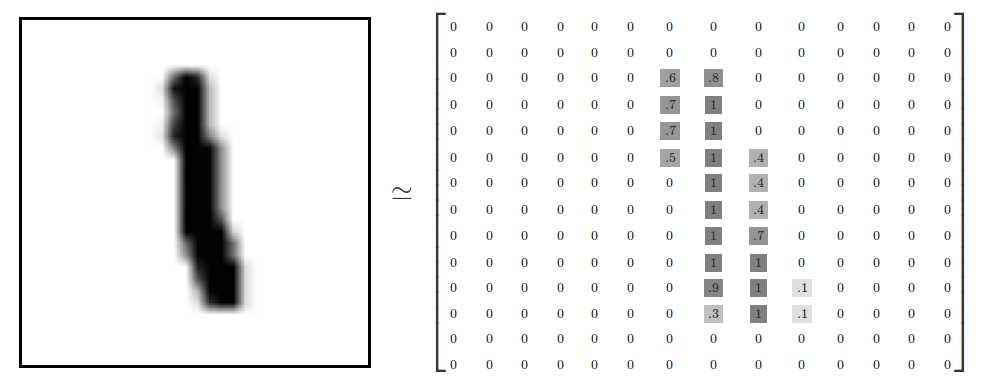
在本次案例中,我们把这个数组展开成一个向量,长度是 28x28 = 784,也就是一个图片就是一行784列的数据,每列中的值是一个像素的灰度值,0-255。
为何要把图像的二维数组转换成一维数组?
把图像的二维数组转换成一维数组一定是把图像中的某些信息给丢弃掉了,但目前本文的案例中也可以用一维数组来进行分类,这个就是深度神经网络的强大之处,它会尽力寻找一堆数据中隐藏的规律。
以后我们会用卷积神经网络来处理这个图像的分类,那时的精确度就能再次进行提高。
但是即便把此图像数据碾平成一维数据的方式也能有一个较好的分辨率。
另外这里有一个关于分类问题的重要概念就是one hot数据,虽然我们对每个图片要打上的标签是0-9数字,但在分类中用一个总共有10个占位分类的数字来表示,如果属于哪个类就在那个位置设置为1,其它位置为0.
例如:
标签0将表示成([1,0,0,0,0,0,0,0,0,0,0])
标签2将表示成([0,0,1,0,0,0,0,0,0,0,0])
这样结果集其实是一个10列的数据,每列的值为0或1。
添加层
添加层的函数跟前面几个博文中一样,这里依然把它贴出来:
def add_layer(inputs, in_size, out_size, activation_function=None):
"""
添加层
:param inputs: 输入数据
:param in_size: 输入数据的列数
:param out_size: 输出数据的列数
:param activation_function: 激励函数
:return:
"""
# 定义权重,初始时使用随机变量,可以简单理解为在进行梯度下降时的随机初始点,这个随机初始点要比0值好,因为如果是0值的话,反复计算就一直是固定在0中,导致可能下降不到其它位置去。
Weights = tf.Variable(tf.random_normal([in_size, out_size]))
# 偏置shape为1行out_size列
biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
# 建立神经网络线性公式:inputs * Weights + biases,我们大脑中的神经元的传递基本上也是类似这样的线性公式,这里的权重就是每个神经元传递某信号的强弱系数,偏置值是指这个神经元的原先所拥有的电位高低值
Wx_plus_b = tf.matmul(inputs, Weights) + biases
if activation_function is None:
# 如果没有设置激活函数,则直接就把当前信号原封不动地传递出去
outputs = Wx_plus_b
else:
# 如果设置了激活函数,则会由此激活函数来对信号进行传递或抑制
outputs = activation_function(Wx_plus_b)
return outputs定义输入数据
xs = tf.placeholder(tf.float32, [None, 28*28])
ys = tf.placeholder(tf.float32, [None, 10]) #10列,就是那个one hot结构的数据定义层
# 定义层,输入为xs,其有28*28列,输出为10列one hot结构的数据,激励函数为softmax,对于one hot类型的数据,一般激励函数就使用softmax
prediction = add_layer(xs, 28*28, 10, activation_function=tf.nn.softmax)定义损失函数
为了训练我们的模型,我们首先需要定义一个指标来评估这个模型是好的。其实,在机器学习,我们通常定义指标来表示一个模型是坏的,这个指标称为成本(cost)或损失(loss),然后尽量最小化这个指标。但是,这两种方式是相同的。
在分类中,我们经常用“交叉熵”(cross-entropy)来定义其损失值,它的定义如下:
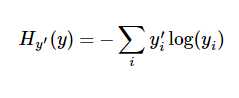
y 是我们预测的概率分布, y‘ 是实际的分布(我们输入的one-hot vector)。比较粗糙的理解是,交叉熵是用来衡量我们的预测用于描述真相的低效性。
# 定义loss值
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf.log(prediction), axis=1))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)初始化变量
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)计算准确度
首先让我们找出那些预测正确的标签。tf.argmax 是一个非常有用的函数,它能给出某个tensor对象在某一维上的其数据最大值所在的索引值。由于标签向量是由0,1组成,因此最大值1所在的索引位置就是类别标签,比如tf.argmax(y_pre,1)返回的是模型对于任一输入x预测到的标签值,而 tf.argmax(v_ys,1) 代表正确的标签,我们可以用 tf.equal 来检测我们的预测是否真实标签匹配(索引位置一样表示匹配)。
correct_prediction = tf.equal(tf.argmax(y_pre, 1), tf.argmax(v_ys, 1))这行代码会给我们一组布尔值。为了确定正确预测项的比例,我们可以把布尔值转换成浮点数,然后取平均值。例如,[True, False, True, True] 会变成 [1,0,1,1] ,取平均值后得到 0.75.
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))最后,我们计算所学习到的模型在测试数据集上面的正确率。
小批量方式进行训练
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={xs: batch_xs, ys: batch_ys})
if i % 50 == 0:
# 每隔50条打印一下预测的准确率
print(computer_accuracy(mnist.test.images, mnist.test.labels))最终打印出:
Extracting D:/todel/python/MNIST_data/train-images-idx3-ubyte.gz
Extracting D:/todel/python/MNIST_data/train-labels-idx1-ubyte.gz
Extracting D:/todel/python/MNIST_data/t10k-images-idx3-ubyte.gz
Extracting D:/todel/python/MNIST_data/t10k-labels-idx1-ubyte.gz
2017-12-13 14:32:04.184392: I C:\tf_jenkins\home\workspace\rel-win\M\windows\PY\36\tensorflow\core\platform\cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: AVX AVX2
0.1125
0.6167
0.741
0.7766
0.7942
0.8151
0.8251
0.8349
0.8418
0.8471
0.8455
0.8554
0.8582
0.8596
0.8614
0.8651
0.8655
0.8676
0.8713
0.8746完整代码
import tensorflow as tf
# 准备数据
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets(‘D:/todel/python/MNIST_data/‘, one_hot=True)
def add_layer(inputs, in_size, out_size, activation_function=None):
"""
添加层
:param inputs: 输入数据
:param in_size: 输入数据的列数
:param out_size: 输出数据的列数
:param activation_function: 激励函数
:return:
"""
# 定义权重,初始时使用随机变量,可以简单理解为在进行梯度下降时的随机初始点,这个随机初始点要比0值好,因为如果是0值的话,反复计算就一直是固定在0中,导致可能下降不到其它位置去。
Weights = tf.Variable(tf.random_normal([in_size, out_size]))
# 偏置shape为1行out_size列
biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
# 建立神经网络线性公式:inputs * Weights + biases,我们大脑中的神经元的传递基本上也是类似这样的线性公式,这里的权重就是每个神经元传递某信号的强弱系数,偏置值是指这个神经元的原先所拥有的电位高低值
Wx_plus_b = tf.matmul(inputs, Weights) + biases
if activation_function is None:
# 如果没有设置激活函数,则直接就把当前信号原封不动地传递出去
outputs = Wx_plus_b
else:
# 如果设置了激活函数,则会由此激活函数来对信号进行传递或抑制
outputs = activation_function(Wx_plus_b)
return outputs
# 定义输入数据
xs = tf.placeholder(tf.float32, [None, 28*28])
ys = tf.placeholder(tf.float32, [None, 10]) #10列,就是那个one hot结构的数据
# 定义层,输入为xs,其有28*28列,输出为10列one hot结构的数据,激励函数为softmax,对于one hot类型的数据,一般激励函数就使用softmax
prediction = add_layer(xs, 28*28, 10, activation_function=tf.nn.softmax)
# 定义loss值
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf.log(prediction), axis=1))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
def computer_accuracy(v_xs, v_ys):
"""
计算准确度
:param v_xs:
:param v_ys:
:return:
"""
# predication是从外部获得的变量
global prediction
# 根据小批量输入的值计算预测值
y_pre = sess.run(prediction, feed_dict={xs:v_xs})
correct_prediction = tf.equal(tf.argmax(y_pre, 1), tf.argmax(v_ys, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
result = sess.run(accuracy, feed_dict={xs:v_xs, ys:v_ys})
return result
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={xs: batch_xs, ys: batch_ys})
if i % 50 == 0:
# 每隔50条打印一下预测的准确率
print(computer_accuracy(mnist.test.images, mnist.test.labels))