问题:磁盘文件排序
输入:
输入的是一个文件,之多包含n个正整数,每个正整数都要小于n,这里n=10^7.每个数字唯一.
输出:
以升序形式输出经过排序的整数列表.
约束:
至多(大约)1MB的可用内存,磁盘空间充足,运行时间只允许几分钟,10s较理想.
解决方案:
(由于约束条件,无法一次性将所有数据读入内存)
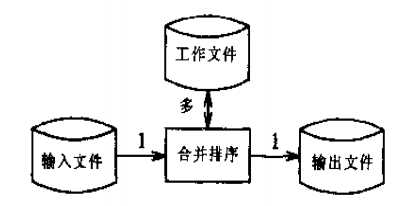
1.基于磁盘的合并排序
思路:分割大文件,分别排序后合并.
步骤:①将文件分割为40个中间文件;
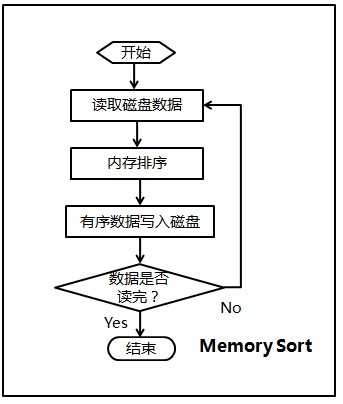
②用内排序将每个中间文件排好序;
③将所有中间文件合并;
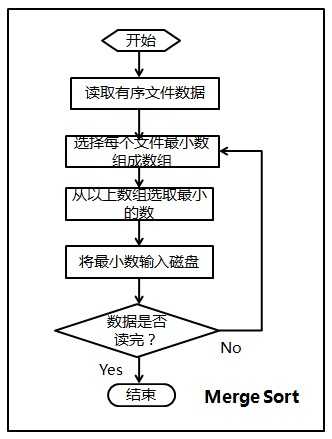
合并思路:
(1)将每个文件最开始的数读入(由于有序,所以为该文件最小数),存放在一个大小为40的first_data数组中;
(2)选择first_data数组中最小的数min_data,及其对应的文件索引index;
(3)将first_data数组中最小的数写入文件result,然后更新数组first_data(根据index读取该文件下一个数代替min_data);
(4)判断是否所有数据都读取完毕,否则返回(2)。
2. 多通道算法
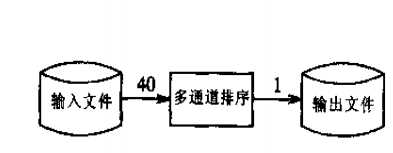
思路:分40次处理数据,第n次读入250000*(n-1)-1~250000*n-1范围内的数,每次排序后写到输出文件.
3. 位图算法
思路:利用位图开关表示数据的存在,一次扫描后将位图中打开的位对应的数字写到输出文件.
步骤:①初始化,将10^7个0写入临时文件;
②扫描输入文件,将数字对应的位打开;
③扫描位图,将打开位对应的数字写到输出文件;
伪代码:
for i = [0,n)
bit[i] = 0
foreach i in the input file
bit[i] = 1
for i = [0,n)
if bit[i] == 1
write i on the output file
(此算法占用内存大约1.2MB,若内存严格限制在1MB,位图算法须做调整,改为基于位图算法的双通道算法,先处理0~4,999,999的数据,再处理5,000,000~9,999,999的数据.)
分析:
1.基于磁盘的归并算法是通用算法,但往往不是最优算法,针对本文的问题,此算法多次磁盘读写,效率低;
2.多通道算法利用了数据的特点(取值范围0~10^7), 需要40次输入和1次输出,效率仍不够高;
3.位图算法对数据特点的依赖性极高,数据要有唯一性,且取值范围要小.对于本文的问题此算法在三种算法中效率最高;
习题:
4.如何高效生成k个小于n且互不重复的正整数,要求数据具有随机性(数字随机且次序随机).
思路:在内存充足的条件下, 在大小为n的数组中依次选取前k个值(保证不重复), 初始时数组中每个数据值为其下标,每次选取一个值之前交换第i个与第randint(i,n-1)个值(保证随机性).
伪代码:
for i = [0,n)
x[i]=i;
for i = [0,k)
swap(i, randint(i,n-1))
print x[i]
6.若每个整数至多出现10次,而不是一次,怎么办?
思路:使用4个位统计它出现的次数,使用10^7/2k bytes 在k通道排序整个文件(k视内存限制而定k越小越快).
9.用更多的空间来换取更少的时间所带来的一个问题就是,初始化空间本身可能要占用大量的时间,如何通过某个技巧绕开这个问题,以便在首次访问某元素时才将其初始化,而不是一开始就初始化整个空间.
思路:使用额外的from和to数组,以及整数top.如果已经初始化data[i],那么from[i]<top且to[from[i]] == i, to和top一起确保了from不会写上内存的随机内容. 实际上这种机制并非100%可靠,可能不幸地出现这种情况:访问data[i],此时并未初始化data[i],但内存上的随机数据恰恰满足了from[i]<top且to[from[i]]==i. 但发生这种状况的几率极小.
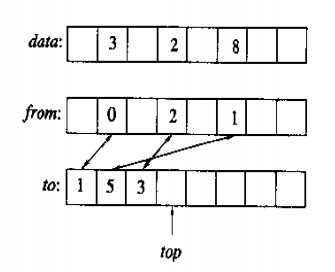
初始化data[i]:
from[i]=top
to[top]=i
data[i]=0
++top
