连续时间信号与离散时间信号之间的关系
下表为各符号的解释
| Symbol | FT | DTFT | Info |
| $x_c(t)$ | $X_c(j\Omega)$ | - | 连续时间信号 |
| $x[n]$ | - | $X(e^{j\omega})$ | 离散时间信号 |
| $s(t)$ | $S(j\Omega)$ | - | 周期脉冲函数、即采样函数 |
| $x_s(t)$ | $X_s(j\Omega)$ | - | 信号周期采样的数学表示 |
| $\Omega_N$ | - | - | 奈奎斯特频率,也就是带限信号的受限频率 |
| $\Omega_s$ | - | - | 采样频率 |
| $T$ | - | - | 采样周期 |
| $h_r(t)$ | $H_r(j\Omega)$ | - | 连续时间低通滤波器 |
| $h[n]$ | - | $H(e^{j\omega})$ | 离散时间单位脉冲响应 |
| $h_c(t)$ | $H_c(j\Omega)$ | 连续时间单位脉冲响应 |
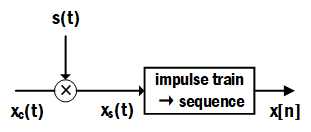
C/D转换
从$x_c(t)$到$x[n]$是一个连续到离散的过程,该过程包括以下步骤:
连续信号$x_c(t)$与采样信号$s(t)$相乘得到采样值加权的周期脉冲$x_s(t)$,最后再经过一步转换才能变成离散的采样序列$x[n]$,这就是一个数学上理想的连续到离散的转换,记为C/D。
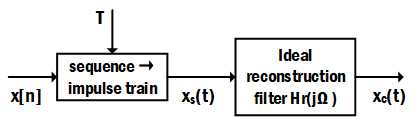
D/C转换
那么反过来,从$x[n]$到$x_c(t)$就是一个离散到连续的过程,该过程包括以下步骤:
离散序列$x[n]$转换成周期为$T$的加权周期脉冲$x_s(t)$,然后就可以按照上一节课所描述的重构方法来得到原连续信号$x_c(t)$,这就是一个数学上理想的离散到连续的转换,记为$D/C$。
连续信号与离散信号的傅里叶变换之间的联系
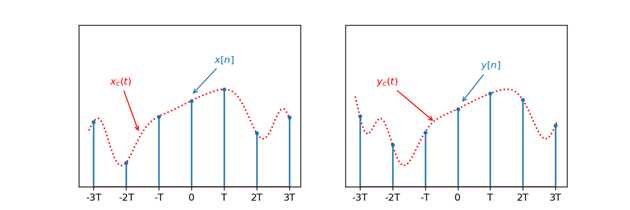
离散时间序列$x[n]$与连续时间信号$x_c(t)$之间有如下关系
$x[n] = x_c(nT)\ ,\ -\infty<n<\infty$
对$x_s(t)$进行傅里叶变换可以得到
$\displaystyle{ X_s(j\Omega) = \sum_{n=-\infty}^{\infty}x_c(nT)e^{-j\Omega T n} = \sum_{n=-\infty}^{\infty}x[n]e^{-j\Omega Tn} }$
对$x[n]$进行离散傅里叶变换可以得到
$\displaystyle{ X(e^{j\omega}) = \sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n} }$
对比发现
$\displaystyle{ X_s(j\Omega) = X(e^{j\omega})|_{\omega = \Omega T} = X(e^{j\Omega T})}$
$X(j\Omega)$相当于$X(e^{j\omega})$进行了一个$\omega = \Omega T$的尺度变换,这是因为$x[n]$的离散时间傅里叶变换的是假设以$1$为周期对信号进行采集的,而这里实际的采集周期为$T$。
另外我们上一课通过傅里叶卷积定理得到了一个公式
$\begin{align*}
X_s(j\Omega) &= \frac{1}{T}X_c*Ш_{\frac{2\pi}{T}}\\
&= \frac{1}{T}X_c(j\Omega)*\sum_{k=-\infty}^{\infty}\delta\left(\Omega-\frac{2\pi k}{T}\right)\\
&= \frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[j\left( \Omega-\frac{2\pi k}{T} \right )\right ]\quad \delta\ convolution\ theorem\\
&= \frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left( j\left( \Omega-k\Omega_s \right) \right) \quad letting\ \Omega_s=\frac{2\pi}{T}
\end{align*}$
结合上述结论,可以得到$x[n]$的DTFT为
$\begin{align*} X(e^{j\omega})|_{\omega=\Omega T}
&= X(e^{j\Omega T})\\
&= X(j\Omega) \\
&= \frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left( j\left( \Omega-k\Omega_s \right) \right) \\
&= \frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[ j\left(\frac{\omega}{T}-\frac{2\pi k}{T} \right )\right ] \qquad \left\{\begin{matrix}\Omega &= &\frac{\omega}{T}\\ \Omega_s &= &\frac{2\pi}{T} \end{matrix} \right.\\
\end{align*}$
也就是说,如果对连续函数$x_c(t)$进行周期为$T$的采样得到离散序列$x[n]$,那么它们的傅里叶变换之间就有以下关系
$\color{red}{\begin{align*} X(e^{j\omega})
&= \frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[ j\left(\Omega-\frac{2\pi k}{T} \right ) \right ]\\
&= \frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[ j\left(\frac{\omega}{T}-\frac{2\pi k}{T} \right )\right ] \qquad \omega=\Omega T
\end{align*}}$
连续时间信号的离散时间处理
在我们生活的世界当中,无论是声音、光、电等都是连续的信号,而计算机处理的是离散信号,因此一般来说我们都需要先把连续信号转换成离散信号,计算机对该离散信号进行处理后再重新转换为连续信号进行输出。
这里假设系统以及输入信号都满足奈奎斯特采样定理。接下来,我们主要讨论离散时间系统是如何对连续信号产生影响的。
频率响应
输出$y_r(t) = \mathcal{F}^{-1}Y_{r}(j\Omega)$,而通过对上图系统的逆推,我们可以得到以下式子
$\begin{align*}
Y_r(j\Omega)
&= H_r(j\Omega)Y(e^{j\omega}) \qquad lowpass\ filter\ H_r(j\Omega)\ for\ restruction\\
&= H_r(j\Omega)H(e^{j\omega})X(e^{j\omega})\qquad LTI\ system\ frequency\ response\ H(e^{j\omega})\\
&= H_r(j\Omega)H(e^{j\Omega T})\frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[j\left(\Omega-\frac{2\pi k}{T} \right )\right ] \\
&=\left\{ \begin{matrix} H(e^{j\Omega T})X_c(j\Omega), & |\Omega|<\pi/T\\ 0,& |\Omega|\geqslant \pi/T\end{matrix}\right.
\qquad because\ H_r(j\Omega) = \left\{\begin{matrix}T, & |\Omega|<\pi/T\\ 0, & |\Omega|\geqslant \pi/T \end{matrix}\right.\\
&= H_{eff}(j\Omega)X_c(j\Omega) \qquad H_{eff}(j\Omega) = \left\{ \begin{matrix} H(e^{j\Omega T}), & |\Omega|<\pi/T\\ 0,& |\Omega|\geqslant \pi/T\end{matrix}\right.
\end{align*}$
从该推导的式子可以得到以下结论
对于一个连续时间信号的离散时间处理系统,如果该系统满足两个因素:
- 离散时间系统的是LTI系统
- 输入信号为带限信号,并且采样率满足奈奎斯特采样定理
则该系统等效于一个连续时间LTI系统,其有效频率响应为
$\color{red}{H_{eff}(j\Omega) = \left\{ \begin{matrix} H(e^{j\Omega T}), & |\Omega|<\pi/T\\ 0,& |\Omega|\geqslant \pi/T\end{matrix}\right.}$
单位脉冲响应
该等式可以说是指出了离散时间系统的频率响应$H(e^{j\Omega T})$以及等效连续时间系统的频率响应$H_c(j\Omega) = H_{eff}(j\Omega)$之间的关系。那么它们的单位脉冲响应之间又具有怎样的关系呢?
这里假设连续时间单位脉冲响应$h_c(t)$与离散时间单位脉冲响应$h[n]$之间有如下关系
$h[n] = h_c(nT)$
那么有
\begin{align*}
H_{eff}(j\Omega) &= \left\{ \begin{matrix} H(e^{j\Omega T}), & |\Omega|<\pi/T\\ 0,& |\Omega|\geqslant \pi/T\end{matrix}\right.\\
&= \left\{ \begin{matrix} \displaystyle{\frac{1}{T}\sum_{k=-\infty}^{\infty}H_{c}\left[j\left( \Omega-\frac{2\pi k}{T} \right)\right]}, & |\Omega|<\pi/T\\ 0,& |\Omega|\geqslant \pi/T\end{matrix}\right.\qquad assume\ h[n]=h_c(nT)\\
&= \left\{ \begin{matrix} \frac{H_c(j\Omega)}{T}, & |\Omega|<\pi/T\\ 0,& |\Omega|\geqslant \pi/T\end{matrix}\right.\\
\end{align*}
因此我们如果稍作调整,假设
$h[n] = Th_c(nT)$
则能使得$H_{eff}(j\Omega) = H_c(j\Omega),|\Omega|<\pi/T$。
离散时间信号的连续时间处理
这种系统相对来说较为罕见,一般不会用这种方法来实现离散时间系统,不过它提供了对某些离散时间系统的一种有用解释,如下面的例子,非整数延迟系统。
这里假设系统以及输入信号都满足奈奎斯特采样定理。因此有
$x_c(t) = \displaystyle{ \sum_{n=-\infty}^{\infty}x[n]\frac{sin[\pi(t-nT)/T]}{\pi(t-nT)/T} }$
$y_c(t) = \displaystyle{ \sum_{n=-\infty}^{\infty}y[n]\frac{sin[\pi(t-nT)/T]}{\pi(t-nT)/T} }$
式中,$x[n] = x_c(nT),y[n] = y_c(nT)$。它们在频域有如下关系(第一小节的结论)
$X_c(j\Omega) = TX(e^{j\Omega T}),\qquad |\Omega|<\pi/T$
$Y_c(j\Omega) = H_c(j\Omega)X_c(j\Omega)$
$Y(e^{j\omega}) = \frac{1}{T}Y_c\left( j\frac{\omega}{T} \right),\qquad |\omega|<\pi$
这三条式子整理后可以得到
$\color{red}{H(e^{j\omega}) = H_c(j\frac{\omega}{T}),\qquad |\omega|<\pi}$
或者可以写成
$\color{red}{H(e^{j\Omega T}) = H_c(j\Omega),\qquad |\Omega|<\pi/T}$
例子
考虑一个离散时间系统,其频率响应为
$H(e^{j\omega}) = e^{-j\omega\Delta}$
当$\Delta$是一个整数时,该系统有一个明确的解释——延迟$\Delta$,即
$y[n] = x[n-\Delta]$
当$\Delta$不是整数时,上面的式子没有正规意义,也无法通过对$x[n]$移位得到输出。此时我们可以用本节学习的内容来进行解释,把该离散时间系统等效为对$x[n]$进行D/C转换后,进行连续时间处理,然后进行C/D转换得到输出。其中的连续时间处理系统的频率响应为
$H_c(j\Omega) = H(e^{j\Omega T}) = e^{-j\Omega T\Delta}$
通过该频率响应可以求得,对于连续时间信号$x_c(t)$以及连续时间信号$y_c(t)$,他们具有如下关系
$y_c(t) = x_c(t-T\Delta)$
其中$x_c(t)$是通过对$x[n]$进行内插得到的,在对$x_c(t)$进行$T\Delta$的延迟后得到$y_c(t)$,然后进行周期为$T$的采样则得到$y[n]$,即
$\begin{align*}
y[n] &=y_c(nT)\\
&= x_c(nT-T\Delta)\\
&= \left.\sum_{k=-\infty}^{\infty}x[k]\frac{sin[\pi(t-T\Delta-kT)/T]}{\pi(t-T\Delta-kT)/T}\right|_{t=nT}\\
&= \sum_{k=-\infty}^{\infty}x[k]\frac{sin\pi(n-k-\Delta)}{\pi(n-k-\Delta)}\qquad
\end{align*}$
按照卷积的定义,该离散时间系统的单位脉冲响应为
$h[n] = \frac{sin\pi(n-\Delta)}{\pi(n-\Delta)}$