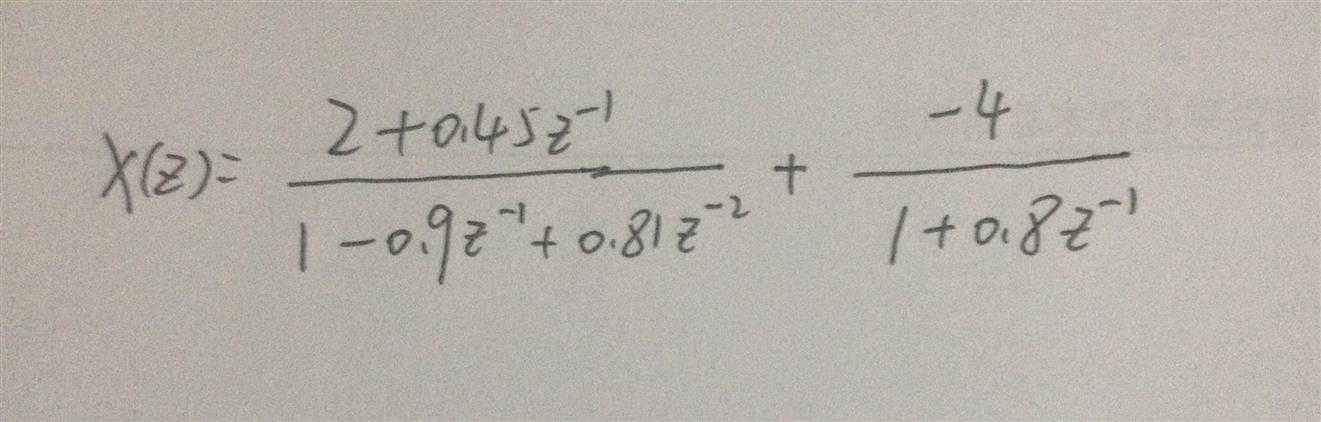代码:
%% ----------------------------------------------------------------------------
%% Output Info about this m-file
fprintf(‘\n***********************************************************\n‘);
fprintf(‘ <DSP using MATLAB> Problem 4.14 \n\n‘);
banner();
%% ----------------------------------------------------------------------------
%format rat;
%% --------------------------------------------------------------------
%% using the method on Page 110 to get the inverse-z transform
%% --------------------------------------------------------------------
b = [-2, 5.65, -2.88];
a = [1, -0.1, 0.09, 0.648];
[R, p, C] = residuez(b, a)
Mp = (abs(p))‘ % pole magnitudes
Ap = (angle(p))‘/pi % pole angle in pi units
[delta, n] = impseq(0, 0, 7);
x_chk = filter(b, a, delta)
figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘Problem 4.14 X(z) pole-zero‘)
set(gcf,‘Color‘,‘white‘);
zplane(b, a);
title(‘pole-zero plot‘); grid on;
%% -----------------------------------------------------------------
%% Now, we use the invCCPP function to get x(n) sequence
%% -----------------------------------------------------------------
[b11, a11] = residuez(R(1:2), p(1:2), C)
b0 = b11(1); b1 = b11(2); % numerator coefficient
a1 = a11(2); a2 = a11(3); % denumerator
[As, Ac, r, v0] = invCCPP(b0, b1, a1, a2);
%% ------------------------------------------------------------------------
%% x1(n)=Ac*(r^n)*cos(pi*v0*n)*u(n) + As*(r^n)*sin(pi*v0*n)*u(n)
%% ------------------------------------------------------------------------
n_start = 0; n_end = 7;
n = [n_start : n_end];
x1 = Ac * (r.^n) .* cos( pi * v0 .* n) .* stepseq(0, n_start, n_end) + As * (r.^n) .* sin(pi * v0 .* n ) .* stepseq(0, n_start, n_end);
x_ori = x1 + R(3)*(p(3).^n) .* stepseq(0, n_start, n_end)
运行结果:
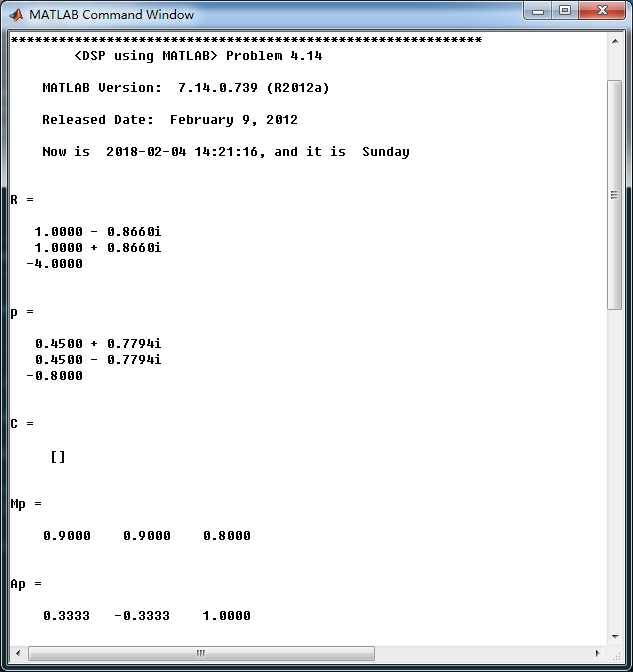
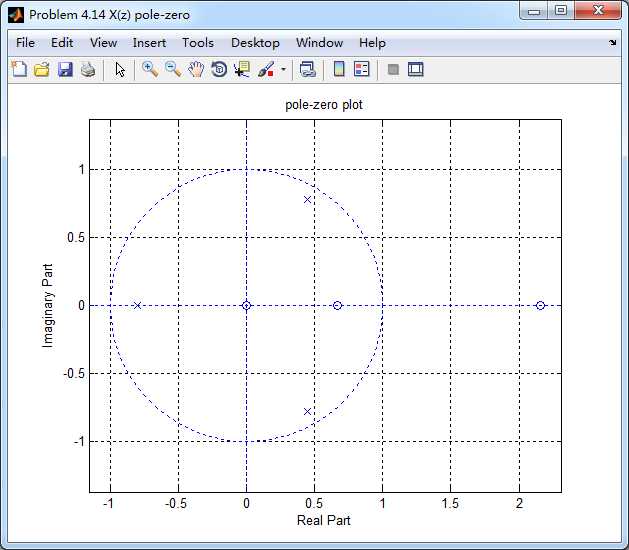
可见有一对复共轭极点和一个实数极点(-0.8),从零极点图也可看出:
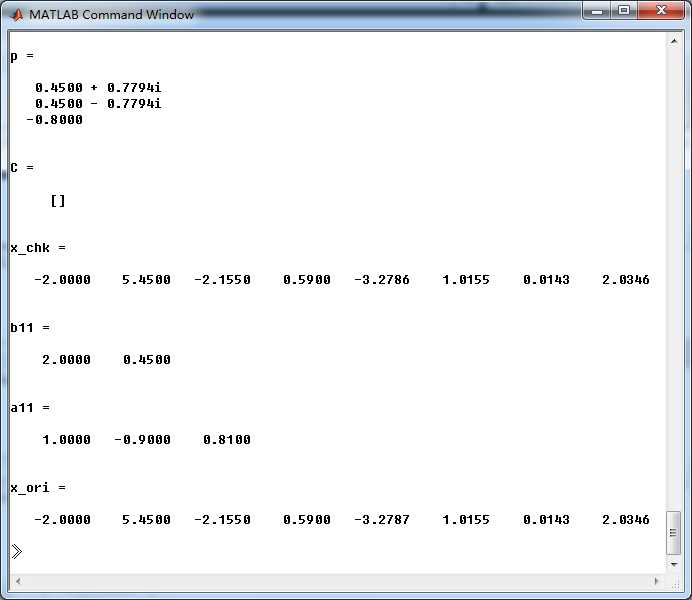
计算一对复共轭极点相对应的有理分式的分子分母的系数b11和a11;这里只显示原始时间序列的前8个元素:
最后写出z变换表达式如下: