Description
考虑一个边权为非负整数的无向连通图,节点编号为1到N,试求出一条从1号节点到N号节点的路径,使得路径上经过的边的权值的XOR和最大。
路径可以重复经过某些点或边,当一条边在路径上出现了多次时,其权值在计算XOR和时也要被计算相应多的次数,具体见样例。
Input
第一行包含两个整数N和 M, 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边,每行三个整数Si,Ti ,Di,表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。
Output
仅包含一个整数,表示最大的XOR和(十进制结果),注意输出后加换行回车。
Sample Input
5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2
Sample Output
6
题面前面一大堆还有一堆都是说XOR计算是什么(然后我就把那一堆删了....)...首先考虑必须从1开始,到N结束,想到这张图可以是由一条路径和一些环构成,那么就随便找出一条从1到N的路径然后再考虑走环的情况。那就先dfs,记录到这个点的异或值,然后每找到一个搜过的点就两个值异或一下求出走一遍当前环的值,然后把所有环的值插进线性基里,初始值为搜出那条路径上的异或和,然后继续从高到低贪心。因为路径可以被计算多次,所以有环不直接挨着主路径也可以,因为走相同的路径就抵消了。所以这个算法应该是对的...
下面代码:
Bzoj 2115: [Wc2011] Xor
Description
考虑一个边权为非负整数的无向连通图,节点编号为1到N,试求出一条从1号节点到N号节点的路径,使得路径上经过的边的权值的XOR和最大。
路径可以重复经过某些点或边,当一条边在路径上出现了多次时,其权值在计算XOR和时也要被计算相应多的次数,具体见样例。
Input
第一行包含两个整数N和 M, 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边,每行三个整数Si,Ti ,Di,表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。
Output
仅包含一个整数,表示最大的XOR和(十进制结果),注意输出后加换行回车。
Sample Input
5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2
Sample Output
6
HINT
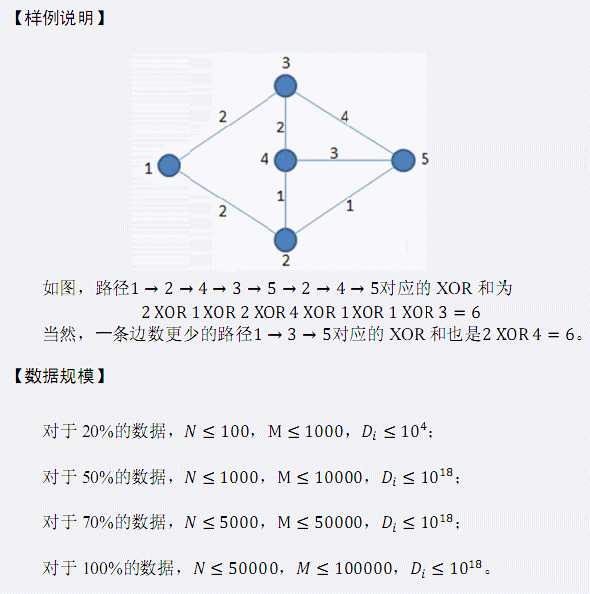
题面前面一大堆都是说XOR计算是什么...首先考虑必须从1开始,到N结束,想到这张图可以是由一条路径和一些环构成,那么就随便找出一条从1到N的路径然后再考虑走环的情况。那就先dfs,记录到这个点的异或值,然后每找到一个搜过的点就两个值异或一下求出走一遍当前环的值,然后把所有环的值插进线性基里,初始值为搜出那条路径上的异或和,然后继续从高到低贪心。因为路径可以被计算多次,所以有环不直接挨着主路径也可以,因为走相同的路径就抵消了。所以这个算法应该是对的...
下面代码:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<iostream> 5 using namespace std; 6 int head[50010],nxt[200010],whr[200010],cnt=1; 7 long long val[200010],dis[50010],in[200010],xian[70]; 8 bool vis[50010]; 9 void add(int a,int b,long long v){ 10 nxt[cnt]=head[a]; 11 whr[cnt]=b; 12 val[cnt]=v; 13 head[a]=cnt++; 14 return; 15 } 16 void dfs(int pos,int pre){ 17 vis[pos]=true; 18 for(int i=head[pos];i;i=nxt[i]){ 19 int t=whr[i]; 20 if(t==pre) continue; 21 if(vis[t]==false){ 22 dis[t]=dis[pos]^val[i]; 23 dfs(t,pos); 24 } 25 else in[++cnt]=dis[t]^dis[pos]^val[i]; 26 } 27 } 28 int main() 29 { 30 int n,m,i,j,a,b; 31 long long v,ans; 32 scanf("%d%d",&n,&m); 33 while(m--){ 34 scanf("%d%d%lld",&a,&b,&v); 35 add(a,b,v);add(b,a,v); 36 } 37 cnt=0; 38 dfs(1,1); 39 ans=dis[n]; 40 for(i=1;i<=cnt;i++){ 41 for(j=60;j>=0;j--){ 42 if((in[i]&(1ll<<j))==0) continue; 43 if(xian[j]==0){ 44 xian[j]=in[i]; 45 break; 46 } 47 in[i]^=xian[j]; 48 } 49 } 50 for(i=60;i>=0;i--) ans=max(ans,ans^xian[i]); 51 printf("%lld",ans); 52 return 0; 53 }
