n(n<=500000)个数,要求维护区间加,区间查询
很简单,用线段树/树状数组随便写写就能过
n(n<=500000)个数,维护插入、删除、找区间第K大/小
用平衡树/set也能过
n(n<=500000)个数,维护区间翻转,区间查询,插入,删除
这个时候就需要用到伸展树(Splay)
splay是一种极(常)灵(数)活(大)的数据结构,它能够维护线段树的部分操作和平衡树的操作
它的美妙之处在于能够旋转,从而完成一系列操作
它的旋转和平衡树的只转一次不同,它可以进行双旋操作来保证较优秀的时间复杂度(但常数还是大)
双旋操作是基于单旋的
首先是单旋:

和平衡树相同
然后是双旋:
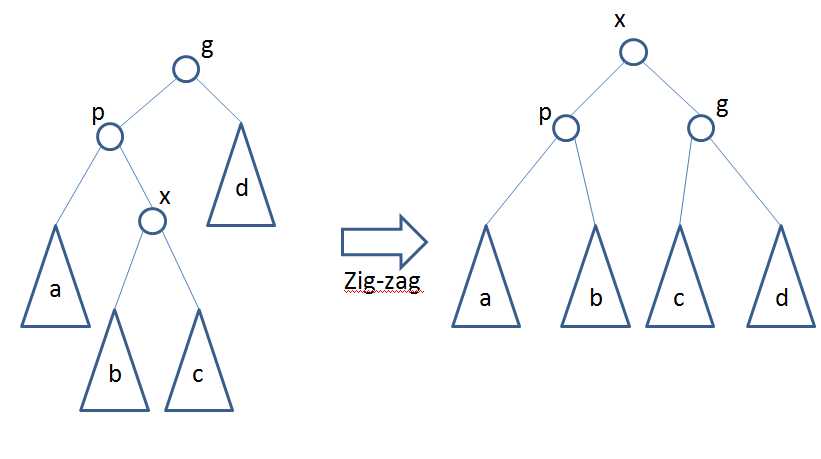
当p不是根节点,且x和p同为左孩子或右孩子时进行Zig-Zig操作。
当x和p同为左孩子时,依次将p和x右旋;
当x和p同为右孩子时,依次将p和x左旋。

当p不是根节点,且x和p不同为左孩子或右孩子时,进行Zig-Zag操作。
当p为左孩子,x为右孩子时,将x左旋后再右旋。
当p为右孩子,x为左孩子时,将x右旋后再左旋。
有了单旋和双旋就可以进行splay操作:
int get(int o){return tree[tree[o].fa].son[1]==o;}
void rotate(QAQ o){
int fa=tree[o].fa,ff=tree[fa].fa;
int pd=get(o);
if(ff) tree[ff].son[get(fa)]=o;
tree[o].fa=ff;
tree[fa].son[pd]=tree[o].son[1-pd];
tree[tree[o].son[1-pd]].fa=fa;
tree[fa].fa=o;tree[o].son[1-pd]=fa;
push_up(fa);push_up(o);
}
void splay(int o,int goal){
//goal是目标节点的父节点,为防止旋转之后导致节点更换带来的影响
while(tree[o].fa!=goal){
int fa=tree[o].fa,ff=tree[fa].fa;
if(ff!=goal) if(tree[ff].son[1]==fa ^ tree[fa].son[1]==o) rotate(o);
else rotate(fa);
rotate(o);
}
if(!goal) rot=o;//换根
push_up(o);
}进行区间操作[l,r]时,常常把节点l-1转到根,r+1转到根的右儿子,这样根的右儿子的左儿子就是操作区间 ,并且常常添加虚拟节点0和n+1来进行[1,n]的操作
区间翻转就直接交换左右儿子
区间加直接加lazy标记
还能查询某一个值的排名:找到节点,转到根,根的做儿子大小+1就是排名
注意:splay中有些操作不能同时进行,例如求第K大和区间操作就不能同时进行,因为前一种操作改变了原序列顺序,后一个操作要求不能改变,这样就发生冲突。splay旋转仅仅是改变树的形状,并没有改变原序列顺序(树的中序遍历)
例题:
bzoj1500 [NOI2005]维护数列
题目描述:
请写一个程序,要求维护一个数列,支持以下 6 种操作:(请注意,格式栏 中的下划线‘ _ ’表示实际输入文件中的空格)

输入输出格式
输入格式:
输入文件的第 1 行包含两个数 N 和 M,N 表示初始时数列中数的个数,M 表示要进行的操作数目。 第 2 行包含 N 个数字,描述初始时的数列。 以下 M 行,每行一条命令,格式参见问题描述中的表格
输出格式:
对于输入数据中的 GET-SUM 和 MAX-SUM 操作,向输出文件依次打印结 果,每个答案(数字)占一行。
输入输出样例
输入样例#1:
9 8 2 -6 3 5 1 -5 -3 6 3
GET-SUM 5 4
MAX-SUM
INSERT 8 3 -5 7 2
DELETE 12 1
MAKE-SAME 3 3 2
REVERSE 3 6
GET-SUM 5 4
MAX-SUM输出样例#1:
-1
10
1
10说明
你可以认为在任何时刻,数列中至少有 1 个数。
输入数据一定是正确的,即指定位置的数在数列中一定存在。
50%的数据中,任何时刻数列中最多含有 30 000 个数;
100%的数据中,任何时刻数列中最多含有 500 000 个数。
100%的数据中,任何时刻数列中任何一个数字均在[-1 000, 1 000]内。
100%的数据中,M ≤20 000,插入的数字总数不超过 4 000 000 。
题解:
对于前5个操作,直接按照splay操作进行
第6个操作,记录左起最长序列、右起最长序列和这个区间的最长序列,合并时通过左右合并
为防止MLE,需要把树上被删除节点回收
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<bitset>
#include<sstream>
#include<cstdlib>
#define QAQ int
#define TAT long long
#define OwO bool
#define ORZ double
#define F(i,j,n) for(QAQ i=j;i<=n;++i)
#define E(i,j,n) for(QAQ i=j;i>=n;--i)
#define MES(i,j) memset(i,j,sizeof(i))
#define MEC(i,j) memcpy(i,j,sizeof(j))
using namespace std;
const QAQ N=1000010;
const QAQ Big=1e6;
QAQ n,m,js,rot,a[N>>1],id[N>>1];
struct data{
QAQ fa,son[2],sum;
QAQ val,size,mx,lx,rx;
OwO rev,lset;
}tree[N];
queue<QAQ> q;
char s[15];
void push_up(QAQ o){
QAQ l=tree[o].son[0],r=tree[o].son[1];
tree[o].sum=tree[l].sum+tree[r].sum+tree[o].val;
tree[o].size=tree[l].size+tree[r].size+1;
tree[o].mx=max(max(tree[l].mx,tree[r].mx),tree[l].rx+tree[r].lx+tree[o].val);
tree[o].lx=max(tree[l].lx,tree[l].sum+tree[r].lx+tree[o].val);
tree[o].rx=max(tree[r].rx,tree[r].sum+tree[l].rx+tree[o].val);
}
void push_down(QAQ o){
QAQ l=tree[o].son[0],r=tree[o].son[1];
if(tree[o].lset){
tree[o].lset=tree[o].rev=0;
if(l) {tree[l].lset=1;tree[l].val=tree[o].val;tree[l].sum=tree[l].size*tree[l].val;}
if(r) {tree[r].lset=1;tree[r].val=tree[o].val;tree[r].sum=tree[r].size*tree[r].val;}
if(tree[o].val>=0){
if(l) tree[l].lx=tree[l].rx=tree[l].mx=tree[l].sum;
if(r) tree[r].lx=tree[r].rx=tree[r].mx=tree[r].sum;
}
else {
if(l) tree[l].lx=tree[l].rx=0,tree[l].mx=tree[l].val;
if(r) tree[r].lx=tree[r].rx=0,tree[r].mx=tree[r].val;
}
}
if(tree[o].rev){
tree[o].rev=0;tree[l].rev^=1;tree[r].rev^=1;
swap(tree[l].lx,tree[l].rx);swap(tree[r].lx,tree[r].rx);
swap(tree[l].son[0],tree[l].son[1]);
swap(tree[r].son[0],tree[r].son[1]);
}
}
void build(QAQ l,QAQ r,QAQ fa){
if(l>r) return ;
QAQ mid=l+r>>1,o=id[mid];
if(l==r){
tree[o].mx=tree[o].sum=a[l];
tree[o].lset=tree[o].rev=0;
tree[o].lx=tree[o].rx=max(a[l],0);
tree[o].size=1;
}
build(l,mid-1,mid);build(mid+1,r,mid);
tree[o].val=a[mid];tree[o].fa=id[fa];
push_up(o);
tree[id[fa]].son[mid>=fa]=o;
}
QAQ find(QAQ o,QAQ x){
push_down(o);
if(tree[tree[o].son[0]].size+1==x) return o;
else if(tree[tree[o].son[0]].size>=x) return find(tree[o].son[0],x);
else return find(tree[o].son[1],x-tree[tree[o].son[0]].size-1);
}
OwO get(QAQ o){return tree[tree[o].fa].son[1]==o;}
void rotate(QAQ o){
QAQ fa=tree[o].fa,ff=tree[fa].fa;
OwO pd=get(o);
if(ff) tree[ff].son[get(fa)]=o;
tree[o].fa=ff;
tree[fa].son[pd]=tree[o].son[1-pd];
tree[tree[o].son[1-pd]].fa=fa;
tree[fa].fa=o;tree[o].son[1-pd]=fa;
push_up(fa);push_up(o);
}
void splay(QAQ o,QAQ goal){
while(tree[o].fa!=goal){
QAQ fa=tree[o].fa,ff=tree[fa].fa;
if(ff!=goal) if(tree[ff].son[1]==fa ^ tree[fa].son[1]==o) rotate(o);
else rotate(fa);
rotate(o);
}
if(!goal) rot=o;
push_up(o);
}
void Insert(QAQ p,QAQ tot){
F(i,1,tot) scanf("%d",&a[i]);
F(i,1,tot) if(q.size()) id[i]=q.front(),q.pop();
else id[i]=++js;
build(1,tot,0);
QAQ l=find(rot,p+1),r=find(rot,p+2);
splay(l,0);splay(r,l);
QAQ rt=id[1+tot>>1];
tree[rt].fa=r;tree[r].son[0]=rt;
push_up(r);push_up(l);
}
QAQ split(QAQ p,QAQ tot){
QAQ l=find(rot,p),r=find(rot,p+tot+1);
splay(l,0);
splay(r,l);
return tree[r].son[0];
}
void recovery(QAQ o){
if(tree[o].son[0]) recovery(tree[o].son[0]);
if(tree[o].son[1]) recovery(tree[o].son[1]);
q.push(o);
tree[o].fa=tree[o].son[0]=tree[o].son[1]=tree[o].lset=tree[o].rev=0;
}
void Del(QAQ p,QAQ tot){
QAQ o=split(p,tot);
QAQ fa=tree[o].fa;
recovery(o);
tree[fa].son[0]=0;
push_up(fa);push_up(tree[fa].fa);
}
void change(QAQ p,QAQ tot,QAQ x){
QAQ o=split(p,tot);
tree[o].val=x;tree[o].lset=1;
tree[o].sum=tree[o].val*tree[o].size;
if(tree[o].val>=0) tree[o].lx=tree[o].rx=tree[o].mx=tree[o].sum;
else tree[o].lx=tree[o].rx=0,tree[o].mx=tree[o].val;
push_up(tree[o].fa);push_up(tree[tree[o].fa].fa);
}
void reverse(QAQ p,QAQ tot){
QAQ o=split(p,tot);
if(!tree[o].lset){
tree[o].rev^=1;
swap(tree[o].son[0],tree[o].son[1]);
swap(tree[o].lx,tree[o].rx);
push_up(tree[o].fa);
push_up(tree[tree[o].fa].fa);
}
}
QAQ get_sum(QAQ p,QAQ tot){
QAQ o=split(p,tot);
return tree[o].sum;
}
QAQ main(){
scanf("%d%d",&n,&m);
F(i,2,n+1) scanf("%d",&a[i]),id[i]=i;
tree[0].mx=a[1]=a[n+2]=-Big;
id[1]=1;id[n+2]=n+2;
build(1,n+2,0);
rot=n+3>>1;js=n+2;
while(m--){
scanf("%s",s+1);
if(s[1]=='I'){
QAQ p,tot;
scanf("%d%d",&p,&tot);
Insert(p,tot);
}
else if(s[1]=='D'){
QAQ p,tot;
scanf("%d%d",&p,&tot);
Del(p,tot);
}
else if(s[1]=='M'&&s[3]=='K'){
QAQ p,tot,x;
scanf("%d%d%d",&p,&tot,&x);
change(p,tot,x);
}
else if(s[1]=='R'){
QAQ p,tot;
scanf("%d%d",&p,&tot);
reverse(p,tot);
}
else if(s[1]=='G'){
QAQ p,tot;
scanf("%d%d",&p,&tot);
printf("%d\n",get_sum(p,tot));
}
else printf("%d\n",tree[rot].mx);
}
return 0;
}bzoj2733 [HNOI2012]永无乡
题目描述
永无乡包含 nn 座岛,编号从 11 到 nn ,每座岛都有自己的独一无二的重要度,按照重要度可以将这 nn 座岛排名,名次用 11 到 nn 来表示。某些岛之间由巨大的桥连接,通过桥可以从一个岛到达另一个岛。如果从岛 aa 出发经过若干座(含 00 座)桥可以 到达岛 bb ,则称岛 aa 和岛 bb 是连通的。
现在有两种操作:
B x y 表示在岛 xx 与岛 yy 之间修建一座新桥。
Q x k 表示询问当前与岛 xx 连通的所有岛中第 kk 重要的是哪座岛,即所有与岛 xx 连通的岛中重要度排名第 kk 小的岛是哪座,请你输出那个岛的编号。
输入输出格式
输入格式:
第一行是用空格隔开的两个正整数 \(n\) 和 \(m\) ,分别表示岛的个数以及一开始存在的桥数。
接下来的一行是用空格隔开的 \(n\) 个数,依次描述从岛 \(1\) 到岛 \(n\) 的重要度排名。随后的 \(m\) 行每行是用空格隔开的两个正整数\(a_i\)和\(b_i\) ,表示一开始就存在一座连接岛 \(a_i\)和岛\(b_i\)的桥。
后面剩下的部分描述操作,该部分的第一行是一个正整数 \(q\) ,表示一共有 \(q\) 个操作,接下来的 \(q\) 行依次描述每个操作,操作的 格式如上所述,以大写字母 \(Q\) 或 \(B\) 开始,后面跟两个不超过 \(n\) 的正整数,字母与数字以及两个数字之间用空格隔开。
输出格式:
对于每个 Q x k 操作都要依次输出一行,其中包含一个整数,表示所询问岛屿的编号。如果该岛屿不存在,则输出 \(-1\)。
输入输出样例
输入样例#1:
5 1
4 3 2 5 1
1 2
7
Q 3 2
Q 2 1
B 2 3
B 1 5
Q 2 1
Q 2 4
Q 2 3输出样例#1:
-1
2
5
1
2说明
对于 20% 的数据 \(n \leq 1000, q \leq 1000n≤1000,q≤1000\)
对于 100% 的数据 \(n \leq 100000, m \leq n, q \leq 300000 n≤100000,m≤n,q≤300000\)
题解:
首先,连通性可以用并查集维护
至于连接,暴力启发式合并就可以了
然后直接写splay
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<bitset>
#include<sstream>
#include<cstdlib>
#define QAQ int
#define TAT long long
#define OwO bool
#define ORZ double
#define F(i,j,n) for(QAQ i=j;i<=n;++i)
#define E(i,j,n) for(QAQ i=j;i>=n;--i)
#define MES(i,j) memset(i,j,sizeof(i))
#define MEC(i,j) memcpy(i,j,sizeof(j))
using namespace std;
const QAQ N=100005;
QAQ n,m,rot,fa[N];
struct data{
QAQ fa,son[2],val,size;
data(){
fa=0;son[1]=son[0]=0;val=0;size=0;
}
}tree[N];
queue<QAQ> q;
QAQ find(QAQ x){return fa[x]==x ? x : fa[x]=find(fa[x]);}
void push_up(QAQ o){tree[o].size=tree[tree[o].son[1]].size+tree[tree[o].son[0]].size+1;}
OwO get(QAQ o){return tree[tree[o].fa].son[1]==o;}
void rotate(QAQ o){
QAQ fa=tree[o].fa,ff=tree[fa].fa;
OwO pd=get(o);
if(ff) tree[ff].son[get(fa)]=o;
tree[o].fa=ff;
tree[fa].son[pd]=tree[o].son[1-pd];
tree[tree[o].son[1-pd]].fa=fa;
tree[fa].fa=o;tree[o].son[1-pd]=fa;
push_up(fa);push_up(o);
}
void splay(QAQ o,QAQ goal){
while(tree[o].fa!=goal){
QAQ fa=tree[o].fa,ff=tree[fa].fa;
if(ff!=goal) if(tree[fa].son[1]==o ^ tree[ff].son[1]==fa) rotate(o);
else rotate(fa);
rotate(o);
}
if(!goal) rot=o;
push_up(o);
}
void Insert(QAQ x){
QAQ t=rot;
while(1){
if(tree[x].val<tree[t].val) if(!tree[t].son[0]){
tree[t].son[0]=x;
tree[x].fa=t;
splay(x,0);
return ;
}
else t=tree[t].son[0];
else if(!tree[t].son[1]) {
tree[t].son[1]=x;
tree[x].fa=t;
splay(x,0);
return ;
}
else t=tree[t].son[1];
}
}
void Merge(QAQ x,QAQ y){
if(tree[x].size<tree[y].size) swap(x,y);
fa[y]=x;rot=x;
q.push(y);
while(q.size()){
QAQ t=q.front();q.pop();
if(tree[t].son[0]) q.push(tree[t].son[0]);
if(tree[t].son[1]) q.push(tree[t].son[1]);
tree[t].son[0]=tree[t].son[1]=0;
tree[t].size=1;
Insert(t);
}
splay(x,0);
}
QAQ K_th(QAQ o,QAQ x){
if(x>tree[o].size) return -1;
QAQ t=rot;
while(1){
if(tree[tree[t].son[0]].size>=x) t=tree[t].son[0];
else if(tree[tree[t].son[0]].size==x-1) return t;
else x-=(tree[tree[t].son[0]].size+1),t=tree[t].son[1];
}
}
QAQ main(){
scanf("%d%d",&n,&m);
F(i,1,n) scanf("%d",&tree[i].val),fa[i]=i;
rot=0;
F(i,1,m) {
QAQ x,y;
scanf("%d%d",&x,&y);
x=find(x);y=find(y);
if(x==y) continue;
splay(x,0);splay(y,0);
Merge(x,y);
}
scanf("%d",&m);
while(m--){
char c;
QAQ a,b;
cin>>c;scanf("%d%d",&a,&b);
if(c=='B'){
a=find(a);b=find(b);
splay(a,0);splay(b,0);
Merge(a,b);
}
else {
a=find(a);splay(a,0);
printf("%d\n",K_th(a,b));
}
}
return 0;
}