处理实际问题的一般数学方法是,首先提炼出问题的本质元素,然后把它看作一个比现实无限宽广的可能性系统,这个系统中的实质关系可以通过一般化的推理来论证理解,并可归纳成一般公式,而这个一般公式适用于任何特殊情况。
——R.A. Fisher
在一个解决方案的复杂性之中,理论或者概念的部分通常只占有限的一小部分。理论无法做实际的工作——否则它也不成其为理论了。从理论到实用,需要经过一系列的发明。从实用到更加实用、更加通用,往往需要增加更多的复杂性。有时,这一过程远远超越科学的范畴,成为艺术家的乐园。有时,这一过程引入了过多不必要的复杂性,只是因为人类的自私、愚蠢和目光短浅。
科学不会也不能处理奇迹。科学只能处理重复的事件,艺术却不同。艺术是“就是如此”。在一个创作诞生以前,它是
Nothing——它没有来由、毫无征兆;诞生之后,它就是存在,是合理,是自然和美。我们所谈论的算法,作为一门实用的科学,既有科学的一面,也有艺术的一面。作为科学,它的结构可以分析,它的行为可以预测,它的属性可以量化,它的正确性可以证明。作为艺术,在一个算法诞生之后,有时我们只能说“它能工作”,仅此而已;对于它是如何来到这个世界上的,我们一无所知——这里没有“因为……所以……”,也不是简单的从一般到特殊。创造,似乎和生命一般神秘。我们可以给造物穿上漂亮的科学外衣,欣赏它内在的一致性,但是,最让人着迷的创造性的那一部分,却完全无法加以描述。
所以,当我们进行散列表的从理论到实用之旅时,如果你察觉到一些没有解释的跨越,请不要见怪吧。如果没有这些跨越,我们就完全可以设计一个程序发明这些算法,我们所要学习的算法也就完全会是另外一个样子了。
O(n) 查找和 O(1) 查找,两个模型
如果想知道在《伊利亚随笔选》这本书里是否有一个“囿”字,该怎么做呢?我们只有从第一页的第一行开始,一个字一个字地向后看去,直到找到这个字为止。如果直到最后一页的最后一个字都没有找到它,我们就知道这本书里根本没有这个字。所以,这项工作的复杂度是
O(n)。
再假设有这样一本《会计专用字帖》,它只有9页,每一页上有一个大写的数字:
当会计想要练习“柒”字时,只要她事先知道页码和内容的对应关系,就可以直接翻到第7页,实现 O(1) 复杂度的查找。通过这个模型我们知道,要想达成 O(1) 复杂度的查找,必须满足3个条件:
1. 存储单元(例如一页纸)中存储的内容(例如大写数字)与存储单元的地址(例如页码)必须是一一对应的。
2. 这种一一对应的关系(例如大写数字“柒”在第7页)必须是可以预先知道的。
3. 存储单元是可以随机读取的。这里“随机读取”的意思是可以以任意的顺序读取每个存储单元,并且每次读取所需时间都是相同的。与此相对的,读取磁带里的一首歌就不是随机的——想听第5首歌就不如听第一首歌来得那么方便。
在计算机上实现 O(1) 查找
先来看计算机的硬件设备。计算机的内存支持随机存取,从它的名字 RAM(random-access memory) 可以看得出对于这一点它还真有一点引以为傲呢。
既然硬件支持,我们就可以准备在计算机上模拟会计专业字帖了。第一项任务是向操作系统申请9个存储单元。这里有个小问题,我们得到的存储单元的地址很可能并不是从1到9,而是从134456开始的。好在我们并不需要直接跟操作系统打交道,高级语言会为我们搞定这些琐事。当我们使用高级语言创建一个数组时,相当于申请了一块连续的存储空间,数组的下标是每个存储单元(抽象)的地址。这样我们第一个
O(1) 复杂度的容器 SingleIntSet 很容易就可以完成了,它只能存储 0~9 这10个数字:
public class SingleIntSet{ private object[] _values = new object[10]; public void Add(int item) { _values[item] = item; } public void Remove(int item) { _values[item] = null; } public bool Contains(int item) { if (_values[item] == null) return false; else return (int)_values[item] == item; }}测试一下:
static void Main(string[] args){ SingleIntSet set = new SingleIntSet(); set.Add(3); set.Add(7); Console.WriteLine(set.Contains(3)); // 输出 true Console.WriteLine(set.Contains(5)); // 输出 false}新术语:使用高级语言创建了一个整型数组时(例如 int[] values = new
int[10]),我们不再把 values[7] 称为“一个存储单元”,因为存储单元的大小是一个字节,在32位操作系统上,values[7]
的大小是4字节,所以我们要使用一个新术语,把 values[7] 称为 values 数组的一个槽(slot)。
SingleIntSet2(说实话我真不喜欢这个名字,谁会喜欢?!)
新需求!同样只需要保存10个数字,只不过这次不是保存0~9,而是需要保存10~19,怎么办?很简单,实现一个槽里的值与地址的映射函数 H() 即可:
public class SingleIntSet2{ private object[] _values = new object[10]; private int H(int value) { return value - 10; } public void Add(int item) { _values[H(item)] = item; } public void Remove(int item) { _values[H(item)] = null; } public bool Contains(int item) { if (_values[H(item)] == null) return false; else return (int)_values[H(item)] == item; }}测试的时候,使用10~19范围内的数字:
static void Main(string[] args){ SingleIntSet2 set = new SingleIntSet2(); set.Add(13); set.Add(17); Console.WriteLine(set.Contains(13)); // 输出 true Console.WriteLine(set.Contains(15)); // 输出 false}
房子不够住,难道睡马路?
这次,还是存储10个数字,只不过数字的范围是0~19。如何把20个数字存放到10个槽里?还能怎么办,2人住1间咯。略微修改一下 H() 函数,其它代码不变:
public class SingleIntSet3{ private object[] _values = new object[10]; private int H(int value) { if (value >= 0 && value <= 9) return value; else return value - 10; } // ...}测试一下:
static void Main(string[] args){ SingleIntSet3 set = new SingleIntSet3(); set.Add(3); set.Add(17); Console.WriteLine(set.Contains(3)); // 输出 true Console.WriteLine(set.Contains(17)); // 输出 true Console.WriteLine(set.Contains(13)); // 输出 false set.Add(13); Console.WriteLine(set.Contains(13)); // 输出 true Console.WriteLine(set.Contains(3)); // 输出 false. 但是应该输出 true 才对!}最后一行的结果不对!2人住1间是行不通的,数据受不了这委屈。但是米有办法,除非 1) 我们预先知道所有的10个输入;2) 这10个输入一旦决定就不再更改,否则无论怎么设计 H() 函数都无法避免2人住一间的情况,这时我们就说发生了碰撞(collision)。
用链接法处理碰撞
处理碰撞最简单的一个办法是链接法(chaining)。链接法就是让发生碰撞的2人住2间,但是共用1个公共地址。为了简单起见,可以让数组的每个槽都指向一个链表:
public class SingleIntSet4{ private object[] _values = new object[10]; private int H(int value) { if (value >= 0 && value <= 9) return value; else return value - 10; } public void Add(int item) { if (_values[H(item)] == null) { LinkedList<int> ls = new LinkedList<int>(); ls.AddFirst(item); _values[H(item)] = ls; } else { LinkedList<int> ls = _values[H(item)] as LinkedList<int>; ls.AddLast(item); } } public void Remove(int item) { LinkedList<int> ls = _values[H(item)] as LinkedList<int>; ls.Remove(item); } public bool Contains(int item) { if (_values[H(item)] == null) { return false; } else { LinkedList<int> ls = _values[H(item)] as LinkedList<int>; return ls.Contains(item); } }}测试一下,这次得到了正确的结果:
static void Main(string[] args){ SingleIntSet4 set = new SingleIntSet4(); set.Add(3); set.Add(17); Console.WriteLine(set.Contains(3)); // 输出 true Console.WriteLine(set.Contains(17)); // 输出 true Console.WriteLine(set.Contains(13)); // 输出 false set.Add(13); Console.WriteLine(set.Contains(13)); // 输出 true Console.WriteLine(set.Contains(3)); // 输出 true}
如何让21亿人使用10个地址?
好吧,有了链接法,我们有了足够的房子以应对可能发生的碰撞。但是我们仍然希望碰撞发生的几率越小越好,特别是当我们把数值范围由 0~19 扩大到 0~int.MaxValue 时候。有什么办法能把21亿个数值映射成10个数值,并且尽量减少碰撞?
除法散列法
h(k) = k mod m
其中,k为槽中的数值,m是数组的大小(为了简单起见本例中固定为10)。这样我们得到第一个正整数范围内通用的 IntSet:
public class IntSet{ private object[] _values = new object[10]; private int H(int value) { return value % 10; } // 其它部分与 SingleIntSet4 相同}测试一下 IntSet.H() 工作得怎么样:
Console.WriteLine(H(3)); // 输出 3Console.WriteLine(H(13)); // 输出 3Console.WriteLine(H(17)); // 输出 7挖藕,只发生了一次碰撞!它竟然与手写版的 SingleIntSet4.H() 工作得一样好。除法散列法为什么有效呢?魔术一旦揭开谜底总是显得平平无奇:
其一,如果小学课程还想得起来的话,应该还记得再大的数除以10的余数都一定介于0~9之间,以此作为下标访问数组自然不用担心越界啦。
其二,让 h() 得出 1 的 k 的数量与让 h() 得出 2 的 k 的数量相同,这样才不容易产生碰撞。
其三,让 h() 得出 1 的 k 是 1、11、21、31……101、111、121……也就是说导致碰撞的 k 值比较分散。这是很重要的,因为在实际使用 IntSet 的时候,存储的值经常是紧挨着的,譬如年龄、序号、身份证号码等等。
需要注意的是 m 不应是 2 的幂即 2p 的形式,此时 h(k) 将等于 k 的二进制的最低 p 位。以 m = 23 = 8 为例,如下图所示: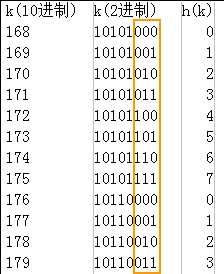
以 k = 170 为例,h(k) = 170 mod 8 = (27 + 25 + 23 + 0*22 + 21 + 0*20) mod 23 = (24*23 + 22*23 + 23 + 0*22 + 21 + 0*20) mod 23 = 0*22 + 21 + 0*20
也就是说只有最低的 p 位不能被 2p
整除。这有什么问题呢?问题是我们不想假设 k 的分布,所以通常希望 h(k) 的值依赖于 k 的所有位而不是最低 p 位。天知道 k
不会是“11010000、00110000、10010000……” 这种样子(假设有个白痴操作系统喜欢先在高位分配一个对象的
Id,而我们又希望把这个 Id 作为 k 的时候,杯具就发生了)。
当用户指定数组的大小之后,我们要找到一个与之最接近的质数作为实际的 m 值,为了速度,我们把常用的质数预存在一张质数表中,新的 IntSet2 允许用户指定它的容量:
public class IntSet2{ private object[] _values; public IntSet2(int capacity) { int size = GetPrime(capacity); _values = new object[size]; } private int H(int value) { return value % _values.Length; } // 质数表 private readonly int[] primes = { 3, 7, 11, 17, 23, 29, 37, 47, 59, 71, 89, 107, 131, 163, 197, 239, 293, 353, 431, 521, 631, 761, 919, 1103, 1327, 1597, 1931, 2333, 2801, 3371, 4049, 4861, 5839, 7013, 8419, 10103, 12143, 14591, 17519, 21023, 25229, 30293, 36353, 43627, 52361, 62851, 75431, 90523, 108631, 130363, 156437, 187751, 225307, 270371, 324449, 389357, 467237, 560689, 672827, 807403, 968897, 1162687, 1395263, 1674319, 2009191, 2411033, 2893249, 3471899, 4166287, 4999559, 5999471, 7199369}; // 判断 candidate 是否是质数 private bool IsPrime(int candidate) { if ((candidate & 1) != 0) // 是奇数 { int limit = (int)Math.Sqrt(candidate); for (int divisor = 3; divisor <= limit; divisor += 2) // divisor = 3、5、7...candidate的平方根 { if ((candidate % divisor) == 0) return false; } return true; } return (candidate == 2); // 除了2,其它偶数全都不是质数 } // 如果 min 是质数,返回 min;否则返回比 min 稍大的那个质数 private int GetPrime(int min) { // 从质数表中查找比 min 稍大的质数 for (int i = 0; i < primes.Length; i++) { int prime = primes[i]; if (prime >= min) return prime; } // min 超过了质数表的范围时,探查 min 之后的每一个奇数,直到发现下一个质数 for (int i = (min | 1); i < Int32.MaxValue; i += 2) { if (IsPrime(i)) return i; } return min; } // 其它部分与 IntSet 相同}注:质数表 primes 和 IsPrime()、GetPrime() 函数都是 Copy 自 .net framwork2.0 源代码的 Hashtable.cs
乘法散列法
h(k) = ?m(kA mod 1)?
其中,A 是一个大于0小于1的常数,例如可以取 A = 2654435769 / 232。kA mod 1 的意思是取 kA 的小数部分。C# 代码可以像这样:
private readonly double A = 2654435769 / Math.Pow(2, 32);int H(int value){ return (int)(_values.Length * (value * A % 1));}关于那个神奇数字的来历以及如何利用计算机的位操作更快地实现 H(),可参见《算法导论》 P138。
乘法散列法的缺点是不如除法散列法那么均匀,可以比较一下 k 取 0~1000 满足 m = 100,h(k)=1 的 k 的分布:
除法散列法,h(k) = k mod 100k h(k) 跨度1 1 -101 1 100201 1 100301 1 100401 1 100501 1 100601 1 100701 1 100801 1 100901 1 100
到目前为止,还有3个遗憾:
1. 只支持正整数。
2. 链接法虽然简单、直接,却不是处理碰撞的唯一的方法。人家 .net framework 的 Hashtable 可是用的更好的开放寻址法。
3. 只能在创建时指定容器的大小,不能自动扩张。
乘法散列法,h(k) = 100*(kA mod 1)k h(k) 跨度34 1 -123 1 89178 1 55267 1 89411 1 144500 1 89644 1 144733 1 89788 1 55877 1 89
让我们喘口气先,这些留在下一篇继续战斗。
散列表(Hash Table)从理论到实用(中)
不用链接法,还有别的方法能处理碰撞吗?扪心自问,我不敢问这个问题。链接法如此的自然、直接,以至于我不敢相信还有别的(甚至是更好的)方法。推动科技进步的人,永远是那些敢于问出比外行更天真、更外行的问题,并且善于运用丰富的想象力找到新的可能性,而且有能力运用科学的方法实践的人。
如果可以不用链表,把节省下来的链表的指针所占用的空间用作空槽,就可以减少碰撞的机会,提高查找速度。
使用开放寻址法处理碰撞
不用额外的链表,以及任何其它额外的数据结构,就只用一个数组,在发生碰撞的时候怎么办呢?答案只能是,再找另一个空着的槽啦!这就是开放寻址法(open addressing)。但是这样难道不是很不负责任的吗?想象一下,有一趟对号入座的火车,假设它只有一节车厢,上来一位坐7号座位的旅客。过了一会儿,又上来一位旅客,他买到的是一张假票,也是7号座位,这时怎么办呢?列车长想了想,让拿假票的旅客去坐8号座位。过了一会儿,应该坐8号座位的旅客上来了,列车长对他说8号座位已经有人了,你去坐9号座位吧。哦?9号早就有人了?10号也有人了?那你去坐11号吧。可以想见,越到后来,当空座越来越少时,碰撞的几率就越大,寻找空座愈发地费劲。但是,如果是火车的上座率只有50%或者更少的情况呢?也许真正坐8号座位的乘客永远不会上车,那么让拿假票的乘客坐8号座位就是一个很好的策略了。所以,这是一个空间换时间的游戏。玩好这个游戏的关键是,让旅客分散地坐在车厢里。如何才能做到这一点呢?答案是,对于每位不同的旅客使用不同的探查序列。例如,对于旅客
A,探查座位 7,8,23,56……直到找到一个空位;对于旅客B,探查座位 25,66,77,1,3……直到找到一个空位。如果有 m
个座位,每位旅客可以使用 <0, 1, 2, ..., m-1> 的 m!
个排列中的一个。显而易见,最好减少两个旅客使用相同的探查序列的情况。也就是说,希望把每位旅客尽量分散地映射到 m! 种探查序列上。换句话说,理想状态下,如果能够让每个上车的旅客,使用 m! 个探查序列中的任意一个的可能性是相同的,我们就说实现了一致散列。(这里没有用“随机”这个词儿,因为实际是不可能随机取一个探查序列的,因为在查找这名旅客时还要使用相同的探查序列)。
真正的一致散列是难以实现的,实践中,常常采用它的一些近似方法。常用的产生探查序列的方法有:线性探查,二次探查,以及双重探查。这些方法都不能实现一致散列,因为它们能产生的不同探查序列数都不超过 m2 个(一致散列要求有 m! 个探查序列)。在这三种方法中,双重散列能产生的探查序列数最多,因而能给出最好的结果(注:.net framework 的 HashTable 就是使用的双重散列法)。
在上一篇中,我们实现了一个函数
h(k),它的任务是把数值 k 映射为一个数组(尽量分散)的地址。这次,我们使用开发寻找法,需要实现一个函数 h(k, i),它的任务是把数值
k 映射为一个地址序列,序列的第一个地址是 h(k, 0),第二个地址是 h(k, 1)……序列中的每个地址都要尽可能的分散。
线性探查
有这样一个可以用 10 个槽保存 0~int.MatValue (但是不能处理碰撞)的 IntSet1:
public class IntSet1{ private object[] _values = new object[10]; private int H(int value) { return value % 10; } public void Add(int item) { _values[H(item)] = item; } public void Remove(int item) { _values[H(item)] = null; } public bool Contains(int item) { if (_values[H(item)] == null) return false; else return (int)_values[H(item)] == item; }}现在想用开放寻址法处理碰撞,该怎么改造它?最简单的方法是,如果发现 values[8] 已经被占用了,就看看 values[9] 是否空着,如果 values[9] 也被占用了,就看看 values[0] 是不是还空着。完整的描述是,先使用 H() 函数获取 k 的第一个地址,如果这个地址已被占用,就探查下一个紧挨着的地址,如果还是不能用,就探查下一个紧挨着的地址,如果到达了数组的末尾,就卷绕到数组的开头,如果探查了 m 次还是没有找到空槽,就说明数组已经满了,这就是线性探查(linear probing)。实现代码是:
public class IntSet2{ private object[] _values = new object[10]; private int H(int value) { return value % 10; } private int LH(int value, int i) { return (H(value) + i) % 10; } public void Add(int item) { int i = 0; // 已经探查过的槽的数量 do { int j = LH(item, i); // 想要探查的地址 if (_values[j] == null) { _values[j] = item; return; } else { i += 1; } } while (i <= 10); throw new Exception("集合溢出"); } public bool Contains(int item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 do { j = LH(item, i); if (_values[j] == null) return false; if ((int)_values[j] == item) return true; else i += 1; } while (i <= 10); return false; } public void Remove(int item) { // 有点不太好办 }} 在 Add() 函数中,先探查 LH(value, 0),它等于 H(value),如果发生了碰撞,就继续探查 LH(value,
1),它是 H(value) 的下一个地址,LH() 里面的 “... % 10”的意思是数组最后一个槽的下一个槽是第一个槽的意思。在
Contains() 函数里,使用和 Add() 函数一样的探查序列,如果找到了 item 返回 true;如果遇到了 null,说明 item
不在数组中。
比较麻烦的是 Remove() 函数。不能简单地把要删除的槽设为 null,那样会导致 Contains()
出错。举个例子,如果依次把 3,13,23 添加到 IntSet2 中,会执行 _values[3] = 3,_values[4] =
13,_values[5] = 23。然后,Remove(13) 执行 _values[4] = null。这时,再调用
Contains(23),会依次检查 _values[3]、_values[4]、_values[5] 直到找到 23 或遇到 null,由于
_values[4] 已经被设为 null 了,所以 Contains(23) 会返回 false。有一个解决此问题的方法是,在
Remove(23) 时把 _values[4] 设为一个特殊的值(例如 -1)而不是 null。这样 Contains(23) 就不会在
_values[4] 那里因为遇到 null 而返回错误的 false 了。并且在 Add() 里,遇到 null 或 -1
都视为空槽,修改之后的代码如下:
public class IntSet2{ private object[] _values = new object[10]; private readonly int DELETED = -1; private int H(int value) { return value % 10; } private int LH(int value, int i) { return (H(value) + i) % 10; } public void Add(int item) { int i = 0; // 已经探查过的槽的数量 do { int j = LH(item, i); // 想要探查的地址 if (_values[j] == null || (int)_values[j] == DELETED) { _values[j] = item; return; } else { i += 1; } } while (i <= 10); throw new Exception("集合溢出"); } public bool Contains(int item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 do { j = LH(item, i); if (_values[j] == null) return false; if ((int)_values[j] == item) return true; else i += 1; } while (i <= 10); return false; } public void Remove(int item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 do { j = LH(item, i); if (_values[j] == null) return; if ((int)_values[j] == item) { _values[j] = DELETED; return; } else { i += 1; } } while (i <= 10); }} 但是这种实现 Remove() 函数的方法有个很大的问题。想象一下,如果依次添加 0、1、2、3、4、5、6、7、8、9,然后再
Remove 0、1、2、3、4、5、6、7、8,这时再调用 Contains(0),此函数会依次检查
_values[0]、_values[1]..._values[9],这是完全无法接受的!这个问题先放一放,我们在下一篇还会继续讨论解决这个问题的方法。
线性探查法虽然比较容易实现,但是它有一个叫做一次群集(primary clustering)的问题。就像本文开篇所讨论的,如果
7、8、9
号座位已被占用,下一个上车的旅客,无论他的票是7号、8号还是9号,都会被安排去坐10号;下一个上车的旅客,无论他的票是7号、8号、9号还是10号,都会被安排去坐11号……如果有
i 个连续被占用的槽,下一个空槽被占用的概率就会是 (i +
1)/m,就像血栓一样,一旦堵住,就会越堵越厉害。这样,使用线性探查法,很容易产生一长串连续被占用的槽,导致 Contains()
函数速度变慢。
对于线性探查法,由于初始位置 LH(k, 0) = H(k) 确定了整个探查序列,所以只有 m 种不同的探查序列。
二次探查
可以在发生碰撞时,不像线性探查那样探查下一个紧挨着的槽,而是多偏移一些,以此缓解一次群集的问题。二次探查(quadratic probing)让这个偏移量依赖 i 的平方:
h(k, i) = (h‘(k) + c1i + c2i2) mod m
其中,c1 和 c2 是不为0的常数。例如,如果取 c1 = c2 = 1,二次探查的散列函数为:
private int QH(int value, int i){ return (H(value) + i + i * i) % 10;}对于数值 7,QH() 给出的探查序列是 7、9、3、9……由于初始位置 QH(k, 0) = H(k)
确定了整个探查序列,所以二次探查同样只有 m 种不同的探查序列。通过让下一个探查位置以 i
的平方偏移,不容易像线性探查那样让被占用的槽连成一片。但是,由于只要探查的初始位置相同,探查序列就会完全相同,所以会连成一小片、一小片的,这一性质导致一种程度较轻的群集现象,称为二次群集(secondary clusering)。
双重散列
造成线性探查法和二次探查法的群集现象的罪魁祸首是一旦初始探查位置相同,整个探查序列就相同。这样,一旦出现碰撞,事情就会变得更糟。是什么造成一旦初始探查位置相同,整个探查序列就相同呢?是因为线性探查法和二次探查法都是让后续的探查位置基于初始探查位置(即
H(k))向后偏移几个位置,而这个偏移量,不管是线性的还是二次的,都仅仅是 i 的函数,但是只有 k 是不同的对不对?所以必须想办法让偏移量是
k 的函数才行。以线性探查为例,要想办法让 LH(k, i) 是 k 和 i 的函数,而不是 H(k) 和 i
的函数。说干就干,我们试着把线性探查
H(k) = k % 10
LH(k, i) = (H(k) + i) % 10
改造一下,先试试把 k 乘到 i 上面去,即
H(k) = k % 10
LH(k, i) = (H(k) + i * k) % 10
这有效果吗?很不幸,
LH(k, i) = (H(k) + i * k) % 10
= (H(k) + i * (k%10) % 10
= (H(k) + i * H(k)) % 10
= (H(k) * (1 + i)) % 10
结果 LH(k, i) 还是 H(k) 和 i 的函数。
再试试把 k 加到 i 上,即
H(k) = k % 10
LH(k, i) = (H(k) + i + k) % 10
这个怎么样?
LH(k, i) = (H(k) + i + k) % 10
= (H(k) + i + k%10) % 10
= (H(k) + i + H(k)) % 10
= (2*H(k) + i) % 10
太不幸了,LH(k) 仍然是 H(k) 和 i 的函数。好像怎么折腾都不行,除非把 H(K) 变成乘法散列法,或者使用双重散列(double hashing)法:
h(k, i) = (h1(k) + i*h2(k)) mod m
其中 h1(k) 和 h2(k) 是两个不同的散列函数。例如可以让
h1(k) = k mod 13
h2(k) = k mod 11
h(k, i) = (h1(k) + i*h2(k)) mod 10
这样,h(7, i) 产生的探查序列是 7、4、1、8、5……
h(20, i) 产生的探查序列是 7、6、5、4、3……
这回终于达到了初始探查位置相同,但是后续探查位置不同的目标。
h2(k)
的设计很有讲究,搞不好会无法探查到每个空槽。以刚刚实现的 h(k, i) 为例,h(6, i)
的探查序列是“6、2、8、4、0、6、2、8、4、0”,如果恰巧数组中的“6、2、8、4、0”这几个位置都被占用了,将会导致程序在还有空槽的状态下抛出“集合溢出”的异常。要避免这种情况,要求
h2(k) 与 m 必须互质。可以看一看如果 h2(k) 与 m 不是互质的话,为什么会有无法探查数组的所有的槽的后果。例如 h2(6)=6 与 10 有公约数2,把它们代入 h(k, i):
h(6, i) = (h1(6) + i * h2(6)) mod 10
= (6 + i * 6) mod 10
= (6 + (i * 6) mod 10) mod 10
= (6 + 2*((i*6) mod 5)) mod 10
由于 (i*6) mod 5) 只有 5 个不同的值,所以 h(6, i) 也只有 5 个值。而 h(16, i) = (3 + 5*((i*5) mod 2)) mod 10 只有2个值,真是太糟糕了。
要想让
h2(k) 与 m 互质,有2种方法。一种方法是让 m 为 2 的幂,并且设计一个总是产生奇数的 h2(k),利用的是奇数和 2 的 m
次幂总是互质的原理。另一种方法是让 m 为质数,并设计一个总是产生比 m 小的正整数的 h2(k)。可以这么实现后一种方法:首先使用上一篇实现的
GetPrime() 函数取得一个合适的质数作为 m,然后让
h1(k) = k mod m
h2(k) = 1 + (k mod (m-1))
在 h2(k) 里之所以要把 (k mod (m-1)) 加上个 1 是为了让 h2(k) 永不为0。因为 h2(k) 为 0 会让 i 不起作用,一旦正巧 h1(k) 产生碰撞就无法取得下一个空槽了。
这是一份完整的示例代码,我们将会在下一篇继续完善它:
public class IntSet4{ private object[] _values; private readonly int DELETED = -1; public IntSet4(int capacity) { int size = GetPrime(capacity); _values = new object[size]; } // 质数表 private readonly int[] primes = { 3, 7, 11, 17, 23, 29, 37, 47, 59, 71, 89, 107, 131, 163, 197, 239, 293, 353, 431, 521, 631, 761, 919, 1103, 1327, 1597, 1931, 2333, 2801, 3371, 4049, 4861, 5839, 7013, 8419, 10103, 12143, 14591, 17519, 21023, 25229, 30293, 36353, 43627, 52361, 62851, 75431, 90523, 108631, 130363, 156437, 187751, 225307, 270371, 324449, 389357, 467237, 560689, 672827, 807403, 968897, 1162687, 1395263, 1674319, 2009191, 2411033, 2893249, 3471899, 4166287, 4999559, 5999471, 7199369}; // 判断 candidate 是否是质数 private bool IsPrime(int candidate) { if ((candidate & 1) != 0) // 是奇数 { int limit = (int)Math.Sqrt(candidate); for (int divisor = 3; divisor <= limit; divisor += 2) // divisor = 3、5、7...candidate的平方根 { if ((candidate % divisor) == 0) return false; } return true; } return (candidate == 2); // 除了2,其它偶是全都不是质数 } // 如果 min 是质数,返回 min;否则返回比 min 稍大的那个质数 private int GetPrime(int min) { // 从质数表中查找比 min 稍大的质数 for (int i = 0; i < primes.Length; i++) { int prime = primes[i]; if (prime >= min) return prime; } // min 超过了质数表的范围时,探查 min 之后的每一个奇数,直到发现下一个质数 for (int i = (min | 1); i < Int32.MaxValue; i += 2) { if (IsPrime(i)) return i; } return min; } int H1(int value) { return value % _values.Length; } int H2(int value) { return 1 + (value % (_values.Length - 1)); } int DH(int value, int i) { return (H1(value) + i * H2(value)) % _values.Length; } public void Add(int item) { int i = 0; // 已经探查过的槽的数量 do { int j = DH(item, i); // 想要探查的地址 if (_values[j] == null || (int)_values[j] == DELETED) { _values[j] = item; return; } else { i += 1; } } while (i <= _values.Length); throw new Exception("集合溢出"); } public bool Contains(int item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 do { j = DH(item, i); if (_values[j] == null) return false; if ((int)_values[j] == item) return true; else i += 1; } while (i <= _values.Length); return false; } public void Remove(int item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 do { j = DH(item, i); if (_values[j] == null) return; if ((int)_values[j] == item) { _values[j] = DELETED; return; } else { i += 1; } } while (i <= _values.Length); }}
除了链接法和开放寻址法,还有更好的方法吗?人类永远不会停止追问,本篇却必须结束了。下一篇,我们将参考 .net framework 源代码,讨论实现散列表的一些重要的细节问题。
散列表(Hash Table) 从理论到实用(下)
【澈丹,我想要个钻戒。】【小北,等等吧,等我再修行两年,你把我烧了,舍利子比钻戒值钱。】
——自扯自蛋
无论开发一个程序还是谈一场恋爱,都差不多要经历这么4个阶段:
1)从零开始。没有束缚的轻松感。似乎拥有无限的可能性,也有相当多的不确定,兴奋、紧张和恐惧。
2)从无到有。无从下手的感觉。一步一坎,进展缓慢。走弯路,犯错,投入很多产出很少。目标和现实之间产生强大的张力。疑惑、挫败、焦急和不甘心。
3)渐入佳境。快速成长。创新,充实,满足。但是在解决问题的同时往往会不可避免地引入更多的问题和遗憾。
4)接近成功。已经没有那么多的新鲜感和成就感,几乎是惯性般地努力前行。感觉成功在望,但又好像永远也不能100%搞定。有时,一心想要完成的欲望甚至超越了原本的目标。
经过前面2篇,我们也来到了第4阶段。让我们深吸一口气,把遗留下来的这几个问题全部搞定吧。
1)能不能支持所有的对象而不仅限于整数?
2)如何支持所有整数而不只是正整数?
3)被删除了的槽仍然占用查找时间。
4)随着时间的推移,被标记为碰撞的槽越来越多,怎么办?
5)必须在创建容器的时候指定大小,不能自动扩张。
6)只是一个 HashSet,而不是HashTable。
继续改造上一篇最后给出的 IntSet4。
支持所有对象而不仅限于整数
要想支持所有对象而不只是整数,就需要一个能把各种类型的对象变换成整数的方法。这一点得到了
.net 特别的优待,Object 类的 GetHashCode()
就是专门干这个的。它提供的默认实现是:对于引用类型,每创建一个新对象都会把Object里的一个内部的计数器增加1,并把计数器的值作为这个对象的
HashCode;对于 struct 对象,将基于每个字段的 HashCode 计算得出一个整型值作为对象的 HashCode。Object
的子类型可以 override GetHashCode() 函数,对于整数类型的变量,GetHashCode()
的返回值与变量的值相同;小数、字符串等都有自己的变换规则(至于具体的规则限于篇幅将不再详细介绍)。总之,我们只要调用对象的
GetHashCode() 函数,把得到的整型值作为 k 的值就行了。另外还需要一个 Object 类型的变量 Key
保存添加的对象,我们把这两个变量封装到一个名为 Bucket 的 struct 里,Add()、Remove()、Contains()
函数也要做相应的修改:
public class HashSet1{ [DebuggerDisplay("Key = {Key} k = {k}")] private struct Bucket { public Object Key; public int k; // Store hash code; } private Bucket[] _buckets; private readonly int DELETED = -1; private int GetHashCode(Object key) { return key.GetHashCode(); } public HashSet1(int capacity) { int size = GetPrime(capacity); _buckets = new Bucket[size]; } public void Add(Object item) { int i = 0; // 已经探查过的槽的数量 Bucket bucket = new Bucket { Key = item, k = GetHashCode(item) }; do { int j = DH(bucket.k, i); // 想要探查的地址 if (_buckets[j].Key == null || _buckets[j].k == DELETED) { _buckets[j] = bucket; return; } else { i += 1; } } while (i <= _buckets.Length); throw new Exception("集合溢出"); } public bool Contains(Object item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 int hashCode = GetHashCode(item); do { j = DH(hashCode, i); if (_buckets[j].Key == null) return false; if (_buckets[j].k == hashCode && _buckets[j].Key.Equals(item)) return true; else i += 1; } while (i <= _buckets.Length); return false; } public void Remove(Object item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 int hashCode = GetHashCode(item); do { j = DH(hashCode, i); if (_buckets[j].Key == null) return; if (_buckets[j].k == hashCode && _buckets[j].Key.Equals(item)) { _buckets[j].k = DELETED; return; } else { i += 1; } } while (i <= _buckets.Length); } // 其它部分与 IntSet4 相同}
让 HashSet 支持所有整数
GetHashCode()
的返回值是 int 类型,也就是说可能为负数。这时,因为数组的大小 m 是正数,所以由 k mod m
计算得出的数组下标也为负数,这可不行。解决方法是先把GetHashCode() 的返回值变换成正数再赋值给 k,最直接的做法是:
int t = key.GetHashCode();
uint k = (uint)t;
由于负数在计算机里以补码的形式保存,所以当 t 是负数时,相当于 k = uint.MaxValue - |t| + 1。这个方案的好处是能够利用 0 ~ uint.MaxValue 范围内的所有整数,更不容易发生碰撞。
不过 .net framework 的 HashTable 却是:
int t = key.GetHashCode();
int k = t & 0x7FFFFFFF; // 把 t 的最高位设为0
由于负数在计算机里以补码的形式保存,所以当 t
是负数时,相当于 k = int.MaxValue - |t| + 1。这个方案的缺点是如果添加 -9 和 2147483639
这两个数字就会发生碰撞,但是因为实际的输入总是比较扎堆的,所以这个缺点也不太容易造成太大的性能问题。它的优点是省下了最高的一个比特位。因为我们在解决问题(3)的时候需要增加一个布尔类型的变量记录是否发生了碰撞,到时候如果利用这个节省下来的比特位,就不用增加一个布尔类型的变量了。按照这个方法修改一下代码:
public class HashSet2{ private int GetHashCode(Object key) { return key.GetHashCode() & 0x7FFFFFFF; } // ...}另外,由于最高的那个比特位有别的用处了,所以不能再把删除的槽的 k 设置成 -1 了,那要设置成什么值好呢? 设置成什么值都不好,因为输入的 k 可能是任何正整数,所以总会有冲突的可能。所以我们改成把 Key 赋值为 _buckets 作为被删除的标志,完整的代码如下:
public class HashSet2{ [DebuggerDisplay("Key = {Key} k = {k}")] private struct Bucket { public Object Key; public int k; // Store hash code; sign bit means there was a collision. } private Bucket[] _buckets; private int GetHashCode(Object key) { return key.GetHashCode() & 0x7FFFFFFF; } // 将 bucket 标记为已删除 private void MarkDeleted(ref Bucket bucket) { bucket.Key = _buckets; bucket.k = 0; } // 判断 bucket 是否是空槽或者是已被删除的槽 private bool IsEmputyOrDeleted(ref Bucket bucket) { return bucket.Key == null || bucket.Key.Equals(_buckets); } public HashSet2(int capacity) { int size = GetPrime(capacity); _buckets = new Bucket[size]; } public void Add(Object item) { int i = 0; // 已经探查过的槽的数量 Bucket bucket = new Bucket { Key = item, k = GetHashCode(item) }; do { int j = DH(bucket.k, i); // 想要探查的地址 if (IsEmputyOrDeleted(ref _buckets[j])) { _buckets[j] = bucket; return; } else { i += 1; } } while (i <= _buckets.Length); throw new Exception("集合溢出"); } public bool Contains(Object item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 int hashCode = GetHashCode(item); do { j = DH(hashCode, i); if (_buckets[j].Key == null) return false; if (_buckets[j].k == hashCode && _buckets[j].Key.Equals(item)) return true; else i += 1; } while (i <= _buckets.Length); return false; } public void Remove(Object item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 int hashCode = GetHashCode(item); do { j = DH(hashCode, i); if (_buckets[j].Key == null) return; if (_buckets[j].k == hashCode && _buckets[j].Key.Equals(item)) { MarkDeleted(ref _buckets[j]); return; } else { i += 1; } } while (i <= _buckets.Length); }}
减少已删除的槽对查找时间的影响
我们在上一篇举过这样一个例子:假设有一个容量
m 为10 的 HashSet,先依次添加 0、1、2、3、4、5、6、7、8、9,然后再删除 0、1、2、3、4、5、6、7、8,这时调用
Contains(0),此函数会依次检查
_values[0]、_values[1]..._values[9],也就是把整个数组遍历了一遍!为什么会这样呢?因为我们在删除一个数字的时候,由于不知道这个数字的后面是否还有一个因与它碰撞而被安排到下一个空槽的数字,所以我们不敢直接把它设为
null。为了解决这个问题,需要一种方法可以指出每个槽是否发生过碰撞。最直接的方法是增加一个 bool
类型的变量,不过为了节省空间,我们将利用在解决问题(2)的时候预留出来的 k
的最高位。如果新添加的项与某个槽发生了碰撞,就把那个槽的碰撞位设为1。有了碰撞位,就可以知道:
1)如果碰撞位为0,说明要么没发生过碰撞,要么它是碰撞链的最后一个槽。
2)如果碰撞位为1,说明它不是碰撞链的最后一个槽。
对于碰撞位为0的槽,删除时可以直接把
Key 设为 null;对于碰撞位为1的槽,因为它不是碰撞链的最后一个槽,所以在删除时还是不能把它的 Key 设为null,而是设为
_buckets 表示已删除,并且要保留 k 的最高位为 1,把 k 的其它位设为0。由于我们其实是把一个 int 类型的变量 _k 当成了一个
bool 类型的变量和一个正整数类型的变量来用,所以要先改造一下 Bucket。(ps:用了很多位操作,要是 C# 也有类似于 C++
的共用体那种东东的话就不用这么麻烦了)
public class HashSet3{ [DebuggerDisplay("Key = {Key} k = {k} IsCollided = {IsCollided}")] private struct Bucket { public Object Key; private int _k; // Store hash code; sign bit means there was a collision. public int k { get { return _k & 0x7FFFFFFF; } // 返回去掉最高的碰撞位之后的 _k set { _k &= unchecked((int)0x80000000); // 将 _k 除了最高的碰撞位之外的其它位全部设为0 _k |= value; // 保持 _k 的最高的碰撞位不变,将 value 的值放到 _k 的后面几位中去 } } // 是否发生过碰撞 public bool IsCollided { get { return (_k & unchecked((int)0x80000000)) != 0; } // _k 的最高位如果为1表示发生过碰撞 } // 将槽标记为发生过碰撞 public void MarkCollided() { _k |= unchecked((int)0x80000000); // 将 _k 的最高位设为1 } } // ...}不需要修改 Contains() 函数,把 Add() 和 Remove() 函数按上面的讨论进行修改:
public class HashSet3{ public void Add(Object item) { int i = 0; // 已经探查过的槽的数量 int k = GetHashCode(item); do { int j = DH(k, i); // 想要探查的地址 if (IsEmputyOrDeleted(ref _buckets[j])) { _buckets[j].Key = item; _buckets[j].k = k; // 仍然保留 _k 的最高位不变 return; } else { _buckets[j].MarkCollided(); i += 1; } } while (i <= _buckets.Length); throw new Exception("集合溢出"); } public void Remove(Object item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 int hashCode = GetHashCode(item); do { j = DH(hashCode, i); if (_buckets[j].Key == null) return; if (_buckets[j].k == hashCode && _buckets[j].Key.Equals(item)) // 找到了想要删除的项 { if (_buckets[j].IsCollided) { // 如果不是碰撞链的最后一个槽,要把槽标记为已删除 MarkDeleted(ref _buckets[j]); } else { // 如果是碰撞链的最后一个槽,直接将 Key 设为 null _buckets[j].Key = null; _buckets[j].k = 0; } return; } else { i += 1; } } while (i <= _buckets.Length); } // ...} 如您所见,一旦被扣上了“发生过碰撞的槽”的帽子,可就一辈子摘不掉了,即使碰撞链的最后一个槽已经被删除了,删除碰撞链的倒数第二个槽时也不会把碰撞位设为0,随着时间的推移,被标记为碰撞过的槽只会越来越多。如果频繁地删完了添、添完了删,发展到极致就可能产生每个槽都被标记为碰撞的情况,这时候
Contains() 函数的复杂度又变成 O(n)
了。解决这个问题的方法是发现被标记为碰撞的槽的超过一定的比例之后,重新排列整个数组,详细的方法会在后面实现容器的自动扩张时一并给出。
我们可以很自然地想到,如果不是使用一个比特来位标记是否发生过碰撞,而是为每个槽增加一个整型变量精确记录发生过多少次碰撞,并且在删除碰撞链的最后一个槽时,把整条碰撞链的每一个槽的碰撞次数减少1,这样就可以完美解决上面那个问题了。这跟垃圾回收机制很像。之所以没有采用这种方法,一是因为这样做会使耗费的存储空间增加1倍,二是因为使用了双重散列法之后,不是很容易产生一长串碰撞链,如果不是特别频繁地删除、添加的话,问题不会很严重。
HashSet 的自动扩张
在数组满了之后,再要添加新项,就得先把数组扩张得大一些。显然,让新数组只比老数组多一个槽是不恰当的,因为那样岂不是以后每添加一个新项都得去扩张数组?那么应该创建多大的新数组才合适呢?目前通常的做法是让新数组比老数组大1倍。
另外,我们在前一篇已经提到过,开放寻址法在座位全部坐满的情况下性能并不好。上座率越低性能越好,但是也越浪费空间。这个上座率——也就是装载因子(_loadFactor)设为多少能达到性能与空间的平衡呢?.net
framework 使用的是 0.72 这个经验值。数组允许添加的项的数量上限 _loadSize = _buckets.Length *
_loadFactor。我们会添加一个整型的变量 _count 记录添加到数组中的项的个数(Add() 时 _count
增加1;Remove() 时 _count 减少1),当检测到 _count >= _loadSize
时就要扩张数组,而不会等到数组满了之后。
还需要添加一个整型变量 _occupancy 用于记录被标记为碰撞的槽的数量。当 _occupancy > _loadSize 时,有可能造成 O(n) 复杂度的查找,所以这时也应该重新排列数组。
首先,添加上面提到那几个变量,并在构造函数里初始化它们:
public class HashSet4{ private int _count = 0; // 添加到数组中的项的总数 private int _occupancy = 0; // 被标记为碰撞的槽的总数 private float _loadFactor = 0.72f; // 装载因子 private int _loadsize = 0; // 数组允许放置的项的数量上限,_loadsize = _bucket.Length * _loadFactor,在确定数组的大小时被初始化。 public HashSet4(int capacity) { int size = GetPrime((int)(capacity / _loadFactor)); if (size < 11) size = 11; // 避免过小的size _buckets = new Bucket[size]; _loadsize = (int)(size * _loadFactor); } // ...}然后实现用于扩张容器的 Expand() 函数和重新排列数组的 Rehash() 函数。因为 Rehash() 函数需要使用新数组的长度计算下标,所以需要改造一下 H1()、H2() 和 DH(),让它们可以接收数组的大小 m 做为参数。Rehash() 与 Add() 函数很像:
public class HashSet4{ private int H1(int k, int m) { return k % m; } private int H2(int k, int m) { return 1 + (k % (m - 1)); } private int DH(int k, int i, int m) { return (H1(k, m) + i * H2(k, m)) % m; } // 扩张容器 private void Expand() { int newSize = GetPrime(_buckets.Length * 2); // buckets.Length*2 will not overflow Rehash(newSize); } // 将老数组中的项在大小为 newSize 的新数组中重新排列 private void Rehash(int newSize) { _occupancy = 0; // 将标记为碰撞的槽的数量重新设为0 Bucket[] newBuckets = new Bucket[newSize]; // 新数组 // 将老数组中的项添加到新数组中 for(int oldIndex = 0; oldIndex < _buckets.Length; oldIndex++) { if (IsEmputyOrDeleted(ref _buckets[oldIndex])) continue; // 跳过已经删除的槽好空槽 // 向新数组添加项 int i = 0; // 已经探查过的槽的数量 do { int j = DH(_buckets[oldIndex].k, i, newBuckets.Length); // 想要探查的地址 if (IsEmputyOrDeleted(ref newBuckets[j])) { newBuckets[j].Key = _buckets[oldIndex].Key; newBuckets[j].k = _buckets[oldIndex].k; break; } else { if (newBuckets[j].IsCollided == false) { newBuckets[j].MarkCollided(); _occupancy++; } i += 1; } } while (true); } // 用新数组取代老数组 _buckets = newBuckets; _loadsize = (int)(newSize * _loadFactor); } // ...}Add() 和 Remove() 需要稍稍修改一下,加上统计 _count 和 _occupancy 的代码,并在需要的时候扩张或重排数组:
public class HashSet4{ public void Add(Object item) { if (_count >= _loadsize) Expand(); // 如果添加到数组中的项数已经到达了上限,要先扩张容器 else if (_occupancy > _loadsize && _count > 100) Rehash(_buckets.Length); // 如果被标记为碰撞的槽的数量和 _loadsize 一般多,就要重新排列所有的项 int i = 0; // 已经探查过的槽的数量 int k = GetHashCode(item); do { int j = DH(k, i, _buckets.Length); // 想要探查的地址 if (IsEmputyOrDeleted(ref _buckets[j])) { _buckets[j].Key = item; _buckets[j].k = k; // 仍然保留 _k 的最高位不变 _count++; return; } else { if (_buckets[j].IsCollided == false) { _buckets[j].MarkCollided(); _occupancy++; } i += 1; } } while (i <= _buckets.Length); throw new Exception("集合溢出"); } public void Remove(Object item) { int i = 0; // 已经探查过的槽的数量 int j = 0; // 想要探查的地址 int hashCode = GetHashCode(item); do { j = DH(hashCode, i, _buckets.Length); if (_buckets[j].Key == null) return; if (_buckets[j].k == hashCode && _buckets[j].Key.Equals(item)) // 找到了想要删除的项 { if (_buckets[j].IsCollided) { // 如果不是碰撞链的最后一个槽,要把槽标记为已删除 MarkDeleted(ref _buckets[j]); } else { // 如果是碰撞链的最后一个槽,直接将 Key 设为 null _buckets[j].Key = null; _buckets[j].k = 0; } _count--; return; } else { i += 1; } } while (i <= _buckets.Length); } // ...}终于完成了一个比较实用的 HashSet 了!附上完整代码:
HashSet 到 HashTable
前面为了简单起见,一直都是只有 Key 而没有 Value。现在我们若想添加一个 Value 简直就跟玩儿似的:
public class HashTable{ [DebuggerDisplay("Key = {Key} k = {k} IsCollided = {IsCollided}")] private struct Bucket { public Object Key; public Object Value; // ... } // ...}当然,Add() 函数也要加上一个 Value 参数,还有按 Key 查找 Value 等等功能限于篇幅就不再啰嗦了。
HashTable 和泛型 Dictionary
在
.net framework 的 HashTable 的源代码的注释里写着“泛型 Dictionary 是 Copy
自 HashTable(The generic Dictionary was copied from Hashtable‘s source -
any bug fixes here probably need to be made to the generic Dictionary as
well.)”,但是瞎了我的极品高清三角眼,怎么看了半天也没找着双重散列的身影呢?除了是泛型的以外,Dictionary 的实现与
HashTable 还有多少不同之处呢?也许下次我们可以一起研究下 Dictionary 的源代码。
