相关概念
- 基本事件ω(也称样本点)：
一次试验可能出现的每一个直接的
结果。也就是随机试验不能够再分解的结果。
如：E1有两个基本事件：E1 ={出现正面}，
E2={出现反面}
E2有六个基本事件： Ei ={出现 i 点}，i=1,2,3,4,5,6
样本空间Ω：全体基本事件的集合。如 E2的样本空间为 Ω={1，2，3，4，5，6}
随机事件：试验的每一个可能结果。
用大写字母A,B,C 等表示
随机事件也就是样本空间的子集，即若干基本事件组成的集合。
如：在E2中，“出现偶数点”的事件可表示为A= {2，4，6}
事件发生：当事件A所包含的基本事件有一个出现，就说事件A发生了，否则就说事件A未发生
必然事件：一定发生的事件，也就是样本空间Ω
不可能事件：一定不发生的事件，记为Φ事件包含：如果事件A发生必然导致事件B发生．则称事件B包含事件A，记作 A? B 或 B ? A
事件的和：事件A与事件B至少有一个发生，这样的一个事件称为事件A 与事件B的和或并，记为A U B 或 A + B
事件的积：事件A与事件B同时发生，这样的事件称为事件A与事件B的积或交，记为A∩B 或 AB
事件的和与积可以推广到多个事件
事件的差：事件A 发生而事件B不发生，这样的事件称为事件A与事件B的差，记为A-B。如A={2,4,6}，B={2,3}，
则A-B={4,6}。 A-B就是A的基本事件中去掉含在B中的，余下的基本事件组成的事件。互斥事件：若事件A与事件B不能同时发生(即AB=Φ)，则称事件A与事件B为互不相容或互斥。若A与B互不相容，就是A与B不含有公共的基本事件
对立事件(互逆)：若事件A与事件B有且仅有一个发生，且AUB=Ω，A∩B=Φ，称事件A与事件B互为对立事件或互逆事件，其中事件B叫做事件A 的逆事件，记作
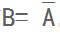，事件A叫做事件B的逆事件，记作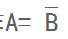
概率的数学定义
设Ω是随机试验E的样本空间，若能找到一个对应法
则，使得对于E的每一事件A都对应一个实数，记为
P(A)，满足：
非负性： P(A)>=0;
正则性： P(Ω)=1;
可列可加性：若A1, A2, ……, An ……互不相容，则
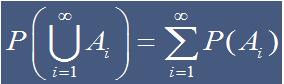
概率的性质和应用
- P(Φ)=0
- 概率有有限可加性：若AB=Φ，则P(AUB) = P(A)+P(B)
可推广到 n 个互不相容事件 - P(A)=1 -
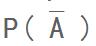
- 对任意两个事件A和B, 有P(B-A)=P(B)-P(AB)
- 对任意两个事件A和B, 有P(AUB)=P(A)+P(B) - P(AB)
例1：每次从 1,2,……,9中取一个数，连续取n次，求
取出的n个数的乘积能被10整除的概率解：因为 “乘积能被10整除” 意味着：
“取到过5”(记为A) 且 “取到过偶数” (记为B)，因此所求概率为 P(AB)
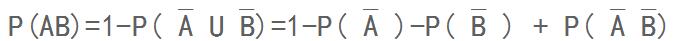
** 即两事件同时发生概率 = 1 - 互逆事件之一发生概率**
=1-(8^n + 5^n - 4^n) / 9^n 条件概率
定义 设E为一试验，A和B为E中两事件，且 P(A)>0，
则称P(AB)/P(A)为事件A发生的条件下事件B发生的条
件概率，记作P(B|A)，即P(B|A)= P(AB)/P(A)例2：袋中有5个球，2个黑球，3个白球，现依次取两
球且不放回，(1)求第二次取到黑球的概率，
(2)若已知第一次取到黑球的条件下，求第二次取到黑球的概率全概率公式----重点
定义 设试验E的样本空间为Ω，事件A1,A2,……,An满足：
- 1°两两互不相容
- 2°ΣAi= Ω
- 3° P(Ai)>0
则称A1,A2,……,An 为 Ω 的一个划分(分割)
定理 设 Ω为试验 E 的样本空间，A 为 E 的一个随机事件，
B1,B2,……,Bn 为Ω的一个划分，且有 P(Bi)>0，则
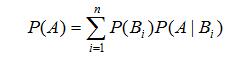
即：事件A发生概率为各个划分的概率乘以在各个划分概率的条件下发生A事件概率的的乘积之和。证明：
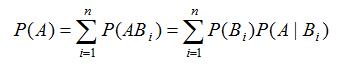
推论：设Ω为E的样本空间，A为E的事件，B1,B2,……,Bn互不
相容，且P(Bi)>0，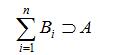
（事件A必然导致各个B事件发生），则
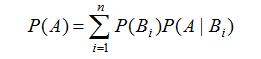
例3：袋中有5个球，2个黑球，3个白球，依次取两球，求第二
次取到黑球的概率- 解：设B1表示“第一次取到黑球”的事件，B2表示“第一次取
到白球”的事件，A 表示事件“第二次取黑球”由全概率公式
有
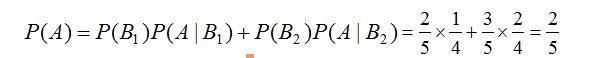
- 解：设B1表示“第一次取到黑球”的事件，B2表示“第一次取
相关概念
一个随机试验的可能结果(称为基本事件)的全体组成一个样本空间Ω。随机变量X是定义于Ω上的函数，即对每一基本事件ω∈Ω，有一数值X(ω)与之对应。以掷一颗骰子的随机试验为例，它的所有可能结果共有6个，分别记作ω1,ω2,ω3,ω4,ω5,ω6,这时，Ω={ω1,ω2,ω3,ω4,ω5,ω6},而出现的点数这个随机变量X，就是Ω上的函数X(ωk)=k，k=1,2,…，6
要全面了解一个随机变量，不但要知道它取哪些值，而且要知 道它取这些值的规律，即要掌握它的概率分布。概率分布可以由分布函数刻画。若知道一个随机变量的分布函数，则它取任何值和它落入某个数值区间内的概率都可以求出。
数学期望---重点
- 数学期望(或均值，亦简称期望)是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量的加权平均值的大小。此处加权即指该随机变量对应的概率。
- 设随机变量X的取值为X1,X2,…..,Xn， P(X1),P(X2),…,P(Xn) 为X对应取值的概率，则：E(X)=X1 P(X1) + X2 P(X2)+…+ Xn P(Xn) =ΣXkP(Xk)
- 例4：扔掷一枚均匀的骰子，直到投出6为止，问平均需要扔掷几次？
解：设Xk为事件：第k次扔掷才投出6，则P(Xk)=1/6(5/6)^(k-1)，
P(k+1)=5/6P(k)
E(X)=1P(1)+2P(2)+……+kP(k)+……=6具体解释：E(X)=1×(1/6)+2×(5/6)×(1/6)+...+k×(5/6)^k-1×(1/6)+...=6
对于第一次：得到6概率为1/6，随机变量为1
对于第二次：第一次没得到6概率是5/6，第二次得到6概率是1/6，随机变量是2
...
解得k=6
