1.定义:
b树是为了硬盘快速读取数据而设计的一种多路查找树。目前大多数数据库及文件索引,都是采用b树来储存实现的。一颗m阶B树满足如下性质:
(1)树中每个节点至多有m颗子树,至少有ceil(m/2)颗子树
(2)树根节点至少有2颗子树
(3)所有叶节点都在同一层
(4)每个节点包括的数据形式是:(N,{key1, key2....keyN},{P0, P1, P2....PN},{Val1,Val2....ValN})其中,N表示关键词key的个数,P表示指向节点子树的指针,Val表示每个key所指向的数据。
2.b树高效的原因:
首先,b树是一颗排序好的树,其结构大致如下:
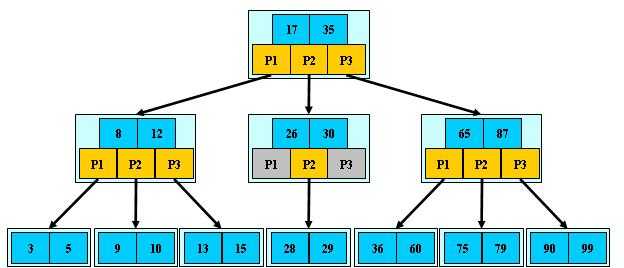
其次,查找B树中的元素,其时间复杂度为O(logN),N为B树中关键词个数。
所以,b树应用在磁盘中时,读取磁盘中指定位置的复杂度仅为O(logN),十分高效!
3.b树的基本概念:
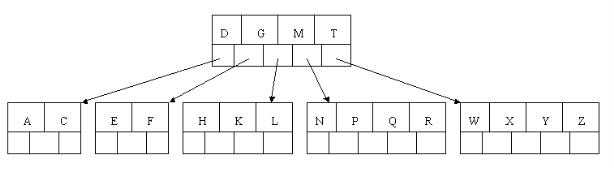
(1)阶数:阶数记做m(m>=2),是最大子节点个数,上图中阶数m=5
(2)关键字:记做key,大小等于节点指向儿子节点的指针个数-1,key<=m-1,上图中D、G、M、T为关键字
(3)度数:记做d或者t,t=ceil( m/2)(PS:ceil(n)函数是求大于等于n的最小整数),上图中度数t=3
每个非根节点至少有t-1个关键 字,至多有2t-1个关键字
4.b树的搜索算法:
设要搜索的数为key,则:从根节点开始,对节点内的关键字二分查找,如果找到则结束;如果没找到,则通过指针(两个关键字之间),进入查询关键词key所属的范围的子节点进行查找。重复查找,直到找到节点对应的儿子指针为空(叶子节点)则查找无结果。
算法代码如下:
int BTreeSearch(TreeNode *root, int k) { if( !root->leaf ) //非叶子节点 { int i=0; while(i<root->key_len && root->key[i] < k) //此处应换为二分查找的方法 i++; if(i<root->key_len && root->key[i] == k) return root->value[i]; //返回key[i]对应的value[i] else return BtreeSearch(root->p[i],k); //递归到k所在的子节点里面找 } else //叶子节点 return -1; //表示没找到 }
由于查找的次数等于:树高*二分查找的次数。时间复杂度为:O(h*O(log n))= O(log n),其中h为B树的高度。总之,B树的查找性能总是等于二分查找的性能 O(log n)。
