1 动态规划的概念:
把问题转变成状态(计算机的本质就是一个状态机,内存里的各种数据构成了当前的状态,CPU只能利用当前的状态去计算下一个状态),并且将状态作为缓存进行存储,当求第 i 个阶段的最优解时,可由前 i-1 个阶段的最优解得到。动态规划的方程是:
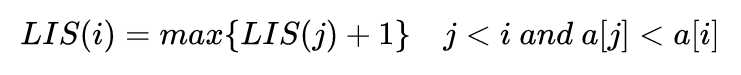
2 动态规划的理解:
先“记忆”之前的某些事情(状态),在求最终目标(最优状态)时,直接使用直接缓存的“记忆”。(“记忆”通过递归的方式存储)
3 动态规划的特点:
- 最优子结构:当子问题最优时,母问题通过一定的选择判断就一定能有最优解的情况。
- 子问题重叠:当母问题和子问题本质上是一个问题的情况。(子问题之间的参数传递是重点!也就是状态转移方程)
- 边界:当某个子问题不再需要提出子子问题就可以得到答案的情况,这个答案就是边界。
4 动态规划和分治的共同点和不同点:
- 共同点:都是把原问题划为若干个子问题,求得子问题的解后,再把子问题的解组合来求得原问题的解。
- 不同点
- 分治用递归的方式求解子问题的解,重复计算子问题解;动态规划则用有记忆功能的递归式(递推),提升了效率。
- 分治的子问题都是独立的(没有公共子问题);动态规划则允许子问题之间有联系,有交叠。
5 解题思路:
当确定问题具有属性:当前状态和之前的状态有关,即母问题可以由最优子问题得到,且子问题是重叠的。可以确定为动态规划问题。
如果问题是要维护一张二维表,首先要确定二维矩阵的行和列各代表什么(背包问题中,行表示物品,列表示包承重)
此时,解题的重点是找到状态转移方程。(说白了要就是递推关系式的确立)
6 背包问题:
问题阐述 n个重量为w1,w2,w3......wn,价值为v1,v2,v3......vn的物品和一个承重为W的背包,求这些物品的最大价值集(能放入背包中)。
问题分析 设F(i,j)为背包问题的最大价值,即:前i个物品放入承重为j的背包中的最大价值。F(i,j)可以看做是一个子问题,他的解可以由之前的子问题的解组合求出。由第i个物品能不能放入承重为j的背包,可以将F(i,j)的解分为两个类别:包含第i个物品和不包含第i个物品:
当j-wi<0,F(i,j)=F(i-1,j) ps:j-wi<0表示第i个物品放不进承重为j的背包中
当j-wi>=0,F(i,j)=max( F(i-1,j), vi+F(i-1,j-wi) ) ps:F(i-1,j)不等于F(i-1,j-wi)
我们的目标就是求得F(n,W)。可以将这个问题看成是二维表的动态规划问题,即:回溯构建一个二维表,将其填满,表的右下角即为问题的解(自底向上的求解方法)
问题求解 采用两种方法,分别是自底向上的求解,以及带有记忆的自顶向下求解。
- 自底向上的动态规划算法:按子问题从小到大的顺序将子问题的解填充到表中,每个子问题都只求解一次。当表填充完毕后,表的右下角的值就是问题的解。
int dp_Backpack(struct backpack bp[n], int W) { int F[n+1][W+1]; for(int i=0;i<n+1;i++) F[i][0] = 0; for(int j=0;j<W+1;j++) F[0][j] = 0; for(int i=1;i<n+1;i++) { for(int j=1;j<W+1;j++) { if(j<bp[i-1].w) F[i][j] = F[i-1][j]; else F[i][j] = max( F[i-1][j], bp[i-1].v+F[i-1][j-bp[i-1].w] ); } } return F[n][W]; }
- 带有记忆的自顶向下动态规划算法:自顶向下的方式求解,①除表中0行和0列的值为0外,初始化表中所有格为null(可以设为-1);②一旦需要某个格中的值,先检查该格,若为null,则递归调用进行计算并记录入表,否则直接从表中取值。ps:避免计算不必要的子问题
struct backpack bp[n] = { //初始化bp结构体数组 } int F[n+1][W+1]; void initF(int F[n+1][W+1]) { for(int i=0;i<n+1;i++) //0列为0 F[i][0] = 0; for(int j=0;j<W+1;j++) //0行为0 F[0][j] = 0; for(int i=0;i<n+1;i++) //剩余表中值初始为-1 for(int j=0;j<W+1;j++) F[i][j] = -1; } int dp_Backpack(int i, int j) { if(F[i][j] == -1) //该值需要递归计算(在表中从上到下的递归计算下来) { if(j < bp[i-1].w) F[i][j] = dp_Backpack(i-1,j); else F[i][j] = max( dp_Backpack(i-1,j) , bp[i-1].v+dp_Backpack(i-1,j-bp[i-1].w) ); } return F[i][j]; } initF(F); int max_val = dp_Backpack(n,W);
完整代码 采用以上两种方法求解01动态规划问题:
#include <iostream> using namespace std; #define N 4 //物品总数 #define C 5 //背包的承重 int w[N] = {2,1,3,2}; //物品重量 int v[N] = {12,10,20,15}; //物品价值 int CurWeight = 0; //当前总重量 int CurValue = 0; //当前总价值 int x[N] ={0,0,0}; //当前的背包选取情况(1表示选取,0表示不选取) int MaxValue = 0; //最大价值 int MaxPack[N] = {0,0,0}; //最大价值下的背包选取情况(1表示选取,0表示不选取) /*用动态规划解决01背包问题*/ int dp_Backpack_1(int NN, int W) { int n = NN+1; int c = W+1; int F[n][c]; for(int i=0;i<n;i++) F[i][0] = 0; for(int j=0;j<c;j++) F[0][j] = 0; for(int i=1;i<n;i++) { for(int j=1;j<c;j++) { if(j<w[i-1]) F[i][j] = F[i-1][j]; else F[i][j] = max( F[i-1][j], v[i-1]+F[i-1][j-w[i-1]] ); } } return F[NN][W]; } /*改进的动态规划求01背包问题*/ void initF(int F[N+1][C+1]) { for(int i=0;i<N+1;i++) F[i][0] = 0; for(int j=0;j<C+1;j++) F[0][j] = 0; for(int i=1; i<N+1; i++) for(int j=1; j<C+1; j++) F[i][j] = -1; } void printF(int F[N+1][C+1]) { for(int i=0; i<N+1; i++) { for(int j=0; j<C+1; j++) cout<<F[i][j]<<" "; cout<<endl; } } int dp_Backpack_2(int F[N+1][C+1], int i, int j) { if(F[i][j] == -1) //该值需要递归计算(在表中从上到下的递归计算下来) { if(j < w[i-1]) F[i][j] = dp_Backpack_2(F,i-1,j); else F[i][j] = max( dp_Backpack_2(F,i-1,j) , v[i-1]+dp_Backpack_2(F,i-1,j-w[i-1]) ); } return F[i][j]; } int main() { cout<<"use dp_1‘s value: "<<dp_Backpack_1(N,C)<<endl; int F[N+1][C+1]; initF(F); cout<<"use dp_2‘s value: "<<dp_Backpack_2(F,N,C)<<endl; printF(F); }
