【BZOJ3774】最优选择
Description
小N手上有一个N*M的方格图,控制某一个点要付出Aij的代价,然后某个点如果被控制了,或者他周围的所有点(上下左右)都被控制了,那么他就算是被选择了的。一个点如果被选择了,那么可以得到Bij的回报,现在请你帮小N选一个最优的方案,使得回报-代价尽可能大。
Input
第一行两个正整数N,M表示方格图的长与宽。
接下来N行每行M个整数Aij表示控制的代价。
接下来N行每行M个整数Bij表示选择的回报。
Output
一个整数,表示最大的回报-代价(如果一个都不控制那么就是0)。
Sample Input
1 100 100
100 1 100
1 100 100
2 0 0
5 2 0
2 0 0
Sample Output
HINT
对于100%的数据,N,M<=50,Aij,Bij都是小于等于100的正整数。
题解:忠告:不要看大爷的图!大爷说的挺明白,然后自己想了一个差不多的建图方法,一看大爷的图:这啥玩应?我和大爷建的不一样啊!一定是我错了!然后试图理解大爷的建图方法,得出结论:大爷太神了,这方法我理解不了。
还是来一个不那么神的,又好想又好理解的做法吧!
黑白染色是显然的啦,对于白点,我们钦定划分到T集代表选,然后讨论所有的情况:
1.四周选,当前点不选。划分到S集,代价0。
因为四周的点是黑点,划分到S集代表不选,而将当前点直接连向四周的点即可保证当前点与T集割开,所以连从当前点到四周的点,容量inf的边。
2.四周不选,当前点选。划分到T集,代价A。
我们需要让当前点花费A的代价即可以与S集割开,所以连从S到当前点,容量为A的边即可。
3.四周不选,当前点不选。划分到S集,代价B。
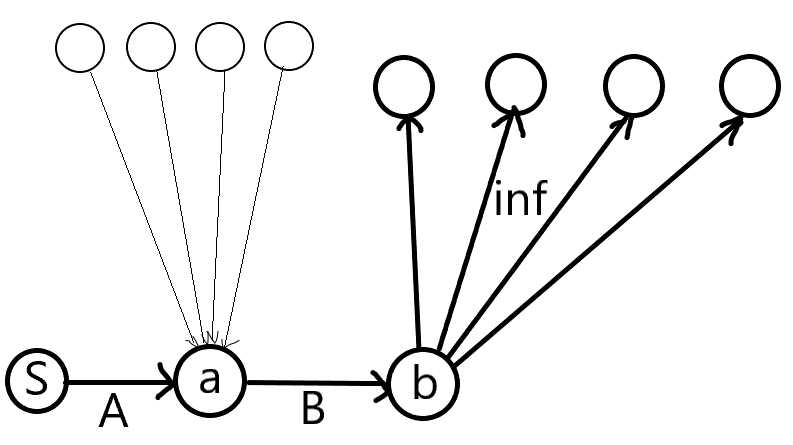
我们需要让当前点花费B的代价即可以与T割开,这个条件和情况1属于【或】关系,所以我们新建点b,设原来的是点a,将1中的边改为从b到四周的点,然后连从a到b,容量为B的边即可。
最终的图其实长这样:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <algorithm>
#define P(X,Y) ((X-1)*m+Y)
#define inf 1<<30
using namespace std;
int n,m,S,T,ans,cnt;
int A[60][60],B[60][60];
int to[100010],next[100010],head[100010],val[100010],d[10010];
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
queue<int> q;
inline void add(int a,int b,int c)
{
to[cnt]=b,val[cnt]=c,next[cnt]=head[a],head[a]=cnt++;
to[cnt]=a,val[cnt]=0,next[cnt]=head[b],head[b]=cnt++;
}
inline int rd()
{
int ret=0,f=1; char gc=getchar();
while(gc<‘0‘||gc>‘9‘) {if(gc==‘-‘) f=-f; gc=getchar();}
while(gc>=‘0‘&&gc<=‘9‘) ret=ret*10+gc-‘0‘,gc=getchar();
return ret*f;
}
inline int dfs(int x,int mf)
{
if(x==T) return mf;
int i,temp=mf,k;
for(i=head[x];i!=-1;i=next[i]) if(val[i]&&d[to[i]]==d[x]+1)
{
k=dfs(to[i],min(temp,val[i]));
if(!k) d[to[i]]=0;
temp-=k,val[i]-=k,val[i^1]+=k;
if(!temp) break;
}
return mf-temp;
}
inline int bfs()
{
memset(d,0,sizeof(d));
while(!q.empty()) q.pop();
d[S]=1,q.push(S);
int i,u;
while(!q.empty())
{
u=q.front(),q.pop();
for(i=head[u];i!=-1;i=next[i]) if(val[i]&&!d[to[i]])
{
d[to[i]]=d[u]+1;
if(to[i]==T) return 1;
q.push(to[i]);
}
}
return 0;
}
int main()
{
n=rd(),m=rd(),S=0,T=2*n*m+1;
int i,j,k,a,b,c;
memset(head,-1,sizeof(head));
for(i=1;i<=n;i++) for(j=1;j<=m;j++) A[i][j]=rd();
for(i=1;i<=n;i++) for(j=1;j<=m;j++) B[i][j]=rd(),ans+=B[i][j];
for(i=1;i<=n;i++) for(j=1;j<=m;j++)
{
if((i^j)&1)
{
a=P(i,j),b=P(i,j)+n*m;
add(S,a,A[i][j]),add(a,b,B[i][j]);
for(k=0;k<4;k++) if(i+dx[k]&&i+dx[k]<=n&&j+dy[k]&&j+dy[k]<=m)
{
c=P(i+dx[k],j+dy[k]),add(b,c,inf);
}
}
else
{
a=P(i,j),b=P(i,j)+n*m;
add(a,T,A[i][j]),add(b,a,B[i][j]);
for(k=0;k<4;k++) if(i+dx[k]&&i+dx[k]<=n&&j+dy[k]&&j+dy[k]<=m)
{
c=P(i+dx[k],j+dy[k]),add(c,b,inf);
}
}
}
while(bfs()) ans-=dfs(0,inf);
printf("%d",ans);
return 0;
}
