对正整数n,欧拉函数是小于n的正整数中与n互质的数的数目(φ(1)=1,φ(2)=1,φ(3)=2 ……)。
例如φ(8)=4,因为1,3,5,7均和8互质。
那么,这个定理有什么用呢???
来看一道题:
欧拉函数(phi)
题目描述:对正整数n,n 的欧拉函数(即φ(N))是少于或等于n 的数中与n 互质的数的数目。例如φ(8)=4,因为1,3,5,7 均和8 互质。
输入
一行一个整数N。
输出
一行一个整数φ(N)
样例输入
8
样例输出
4
哈哈哈,一道裸题,那么我们来仔细分析一下每一步:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <cstdlib> #define N 10010 #define zxy(i , a , b) for(int i = a ; i <= b ; i ++) #define yxz(i , a , b) for(int i = a ; i >= b ; i ++) #define zxyzxy(i , a , b) for(int i = a ; i < b ; i ++) #define yxzyxz(i , a , b) for(int i = a ; i > b ; i ++) using namespace std; typedef long long ll; ll n,ans; ll read() { ll ans = 0; char ch = getchar(),last = ‘ ‘; while(ch < ‘0‘ || ch > ‘9‘) last = ch , ch = getchar(); while(ch >= ‘0‘ && ch <= ‘9‘) ans = ans * 10 +ch - ‘0‘ , ch = getchar(); if(last == ‘-‘) ans =- ans; return ans; } void put(ll x) { if(x < 0) { putchar(‘-‘); x = -x; } if(x == 0) { putchar(‘0‘); return; } int q[100] , nn = 0; while(x) q[++ nn] = x % 10 , x /= 10; while(nn) putchar(‘0‘ + q[nn]), --nn; } int main() { //freopen("phi.in","r",stdin); //freopen("phi.out","w",stdout); n = read(); ans = n; for(int i = 2 ; i * i <= n ; i ++) { if(n % i ==0) ans = ans / i * (i - 1); while(n % i == 0) n /= i; } if(n > 1) ans = ans / n * (n - 1); put(ans); return 0; }
这里有个欧拉的公式:
![]()
即:
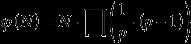
这个就是代码中的:
ans = ans / i * (i - 1);
先除后乘是为了防止溢出。
咱们从头来看这个代码:
i代表n的素因子。因为在后面的循环操作中,把n都变成了他的最小素因子,所以就可以把这个数的n次幂的数都可以删掉,就可以省时间。
i循环到根号n的原因是对于一个正整数n来说,在根号n到n的范围内有且只有一个n的素因子。
为什么呢?用反证法证明一下,如果有两个或两个以上的素因子在这段区间内的话,那么这两个因子的乘积就肯定会大于n,所以假设不成立。
那么这种循环到根号n的做法是既省码速,又省空间的。
因此,在最后要添加一个操作,就是把这个n再求一遍素因子个数。
因为如果假设n分解成的若干个质因数的幂的乘积中的一个单项式特别大的话,那么它就十分接近于n,所以它的指数就肯定是小于2的(上述已证根号n到n只有一个素因子),所以它的指数只能为1,就只要操作一次而不用像上面的用while来维护了。
最后的ans就是phi(n)的解了。
